| Sucesos independientes Dos sucesos son independientes si y sólo si p(A Ç B) = p(A) p(B). Si dos sucesos son independientes Esta propiedad coincide más con la idea intuitiva de independencia y algunos textos la dan como definición. Hay que notar, sin embargo, que ambas definiciones no son estrictamente equivalentes. Ejemplo 7:
Para un hijo de una mujer portadora de Duchenne, el sexo y la enfermedad ¿son independientes?
Según vimos en el Ejemplo 3 el espacio muestral es W = {xX, xY, XX, XY}
Definimos los sucesos A = {varón} = {xY, XY}; B = {enfermo} = {xY} A Ç B = {xY} por lo tanto p(A) = 0,5; p(B) = 0,25; p(A Ç B) = 0,25 ¹ p(A) p(B) NO son independientes.
http://www.hrc.es/bioest/Probabilidad_16.html
En teoría de probabilidades, se dice que dos sucesos aleatorios son independientes entre sí cuando la probabilidad de cada uno de ellos no está influida porque el otro suceso ocurra o no, es decir, cuando ambos sucesos no están relacionados.
Definición formal
Dos sucesos son independientes si la probabilidad de que ocurran ambos simultáneamente es igual al producto de las probabilidades de que ocurra cada uno de ellos, es decir, si
Motivación de la definición
Sean y dos sucesos tales que , intuitivamente A es independiente de B si la probabilidad de A condicionada por B es igual a la probabilidad de A. Es decir si:
De la propia definición de probabilidad condicionada:
se deduce que y dado que deducimos trivialmente que .
Si el suceso A es independiente del suceso B, automáticamente el suceso B es independiente de A.
Propiedades
La independencia de sucesos es algo muy importante para la estadística y es condición necesaria en multitud de teoremas. Por ejemplo, una de las primeras propiedades que se deriva de la definición de sucesos independientes es que si dos sucesos son independientes entre sí, la probabilidad de la intersección es igual al producto de las probabilidades.
INDEPENDENCIA ESTOCÁSTICA DE SUCESOS:
Dos sucesos A y B son estocásticamente independientes cuando la información sobre la ocurrencia de uno de ellos no modifica la probabilidad de que ocurra el otro.Esto es:
P(A/B) = P(A) o equivalentemente P(B/A) = P(B) ejemplo
CARACTERIZACIÓN DE LA INDEPENDENCIA: TEOREMA DE CARACTERIZACIÓN
A y B son independientes Û P(AÇB) = P(A).P(B) ya que si por definición de independencia
y por definición de probabilidad condicionada
deberá cumplirse que
Así , dos sucesos A y B son independientes si y sólo si
GENERALIZACIÓN DEL CONCEPTO DE INDEPENDENCIA (caracterización) PARA n SUCESOS
Un número finito o infinito de sucesos
tales que
Así para tres sucesos
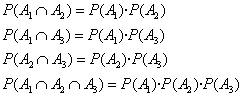 PROPIEDADES:
1.-Si A y B son independientes los complementarios también lo son.
Así Si A y B son independientes se cumplirá que
  para que para que 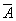 y y
Si
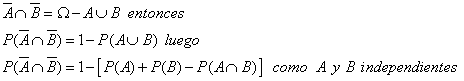
Entonces tendremos que :
luego los complementarios son independientes
2.- Si A y B son independientes el complementario de A y el suceso de B también lo son. (evidentemente el complementarios de B y el suceso A , también)
Si A y B son independientes se cumplirá que
 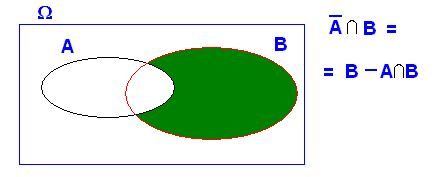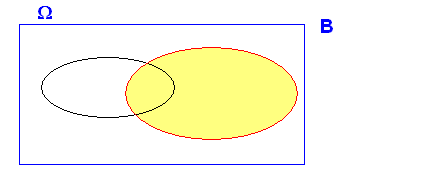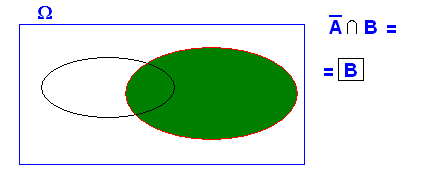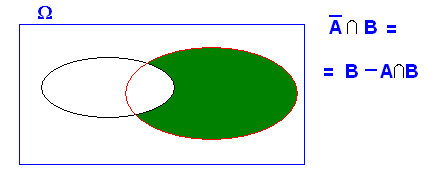 para que para que 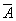 y y ya que : 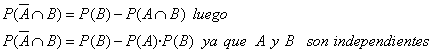
Así :
luego A complementario y B son independientes.
Análogamente el complementario de B y el suceso A también serán independientes si A y B lo son
3.- Si A implica B ( A Í B) , A y B , “NO” son independientes
A y B son independientes si se cumple que
 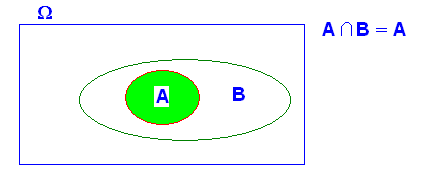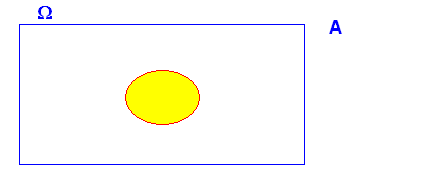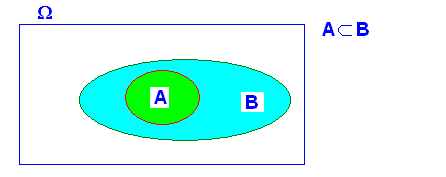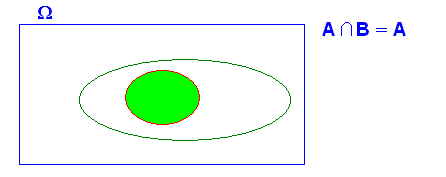 ya que ya que luego A y B No son independientes , salvo en el caso de que en el que
4.-Si dos sucesos son incompatibles-disjuntos (mutuamente excluyentes o de intersección vacía), “NO” son independientes
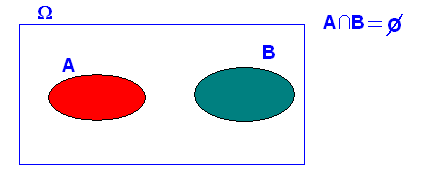 A y B son independientes si se cumple que A y B son independientes si se cumple que 
ya que
luego A y B No son independientes , salvo que P(A) ó P(B) sean 0; caso extremo e inadecuado
|
viernes, 28 de abril de 2017
Bioestadística Clínica
Suscribirse a:
Enviar comentarios (Atom)









No hay comentarios:
Publicar un comentario