CRISTALOGRAFÍA

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

La transformación de una fase de otra por el crecimiento de núcleos que se forman aleatoriamente en la fase principal

La ecuación de Avrami describe cómo los sólidos se transforman de una fase (estado de la materia) a otra a temperatura constante. Puede describir específicamente la cinética de la cristalización , puede aplicarse en general a otros cambios de fase en los materiales, como las velocidades de reacción química, e incluso puede ser significativo en los análisis de sistemas ecológicos. ^[1]

La ecuación también se conoce como la ecuación de Johnson- Mehl -Avrami- Kolmogorov o JMAK. La ecuación fue derivada por primera vez por Kolmogorov en 1937 y popularizada por Melvin Avrami en una serie de artículos publicados en el Journal of Chemical Physics desde 1939 hasta 1941.

Cinética de transformación [ editar ]

Diagrama de transformación isotérmica típica (arriba). La transformación se puede describir usando la ecuación de avrami como una gráfica de lnln (1 / (1-Y)) vs ln (t) produce una línea recta

Con frecuencia, se observa que las transformaciones siguen un perfil característico en forma de s, o sigmoidal, donde las tasas de transformación son bajas al principio y al final de la transformación pero rápidas entre ellas.

La velocidad lenta inicial puede atribuirse al tiempo requerido para que se forme y comience a crecer un número significativo de núcleos de la nueva fase. Durante el período intermedio, la transformación es rápida a medida que los núcleos crecen en partículas y consumen la fase anterior, mientras que los núcleos continúan formándose en la fase principalrestante .

Una vez que la transformación se acerca a su finalización, queda poco material sin transformar para una mayor nucleación y la producción de nuevas partículas comienza a disminuir. Además, las partículas previamente formadas comienzan a tocarse entre sí, formando un límite donde el crecimiento se detiene.

Derivación [ editar ]

La derivación más simple de la ecuación de Avrami hace una serie de suposiciones y simplificaciones significativas: ^[5]

• La nucleación se produce de forma aleatoria y homogénea en toda la parte no transformada del material.
• La tasa de crecimiento no depende del grado de transformación.
• El crecimiento se produce al mismo ritmo en todas las direcciones.

Si se cumplen estas condiciones entonces una transformación de $${\ displaystyle \ alpha \, \!} dentro $${\ displaystyle \ beta \, \!} Se procederá por la nucleación de nuevas partículas a una velocidad. $${\ displaystyle {\ dot {N}} \, \!} por unidad de volumen que crece a un ritmo $${\ displaystyle {\ dot {G}} \, \!}en partículas esféricas y solo dejan de crecer cuando chocan unas con otras. Durante un intervalo de tiempo,{\ displaystyle 0 <\ tau , la nucleación y el crecimiento solo pueden tener lugar en material no transformado. Sin embargo, el problema se resuelve más fácilmente aplicando el concepto de un volumen extendido , el volumen de la nueva fase que se formaría si toda la muestra aún no estuviera transformada. Durante el intervalo de tiempo de τ a τ + dτ, el número de núcleos, N, que aparecen en una muestra del volumen V estará dado por:

$${\ displaystyle N = V {\ dot {N}} d \ tau \, \!} [1]

dónde $${\ displaystyle {\ dot {N}} \, \!}es uno de los dos parámetros en este modelo simple, es la constante de supresión, la tasa de nucleación por unidad de volumen. Dado que el crecimiento es isotrópico, constante y sin obstáculos por el material previamente transformado, cada núcleo crecerá en una esfera de radio$${\ displaystyle {\ dot {G}} (t- \ tau)} y así el volumen extendido de $${\ displaystyle \ beta} Debido a que los núcleos que aparecen en el intervalo de tiempo serán:

$${\ displaystyle dV _ {\ beta} ^ {e} = {\ frac {4 \ pi} {3}} {\ dot {G}} ^ {3} (t- \ tau) ^ {3} V {\ dot {N}} d \ tau \, \!}

dónde $${\ displaystyle {\ dot {G}} \, \!} es el segundo de los dos parámetros de este modelo simple, es la velocidad de crecimiento de un cristal, supuestamente constante. La integración de esta ecuación entre $${\ displaystyle \ tau = 0} y $${\ displaystyle \ tau = t} producirá el volumen extendido total que aparece en el intervalo de tiempo

$${\ displaystyle V _ {\ beta} ^ {e} = {\ frac {\ pi} {3}} V {\ dot {N}} {\ dot {G}} ^ {3} t ^ {4} \, \!}

Sólo una fracción de este volumen extendido es real; una parte del mismo se encuentra en material previamente transformado y es virtual. Dado que la nucleación se produce aleatoriamente, la fracción del volumen extendido que se forma durante cada incremento de tiempo que es real será proporcional a la fracción de volumen de$${\ displaystyle \ alpha}. Así

$${\ displaystyle dV _ {\ beta} = dV _ {\ beta} ^ {e} \ left (1 - {\ frac {V _ {\ beta}} {V}} \ right) \, \!}

reorganizado

$${\ displaystyle {\ frac {1} {1-V _ {\ beta} / V}} dV _ {\ beta} = dV _ {\ beta} ^ {e} \, \!}

y sobre la integración

$${\ displaystyle \ ln (1-Y) = - V _ {\ beta} ^ {e} / V \, \!}

donde Y es la fracción de volumen de $${\ displaystyle \ beta} ($${\ displaystyle V _ {\ beta} / V}).

Dadas las ecuaciones anteriores, esto se puede reducir a la forma más familiar de la ecuación de Avrami (JMAK) que da la fracción de material transformado después de un tiempo de mantenimiento a una temperatura dada

$${\ displaystyle Y = 1- \ exp [-K (t) ^ {n}] \, \!}    dónde    $${\ displaystyle K = \ pi {\ dot {N}} {\ dot {G}} ^ {3} / 3 \, \!}    y    $${\ displaystyle n = 4 \, \!}

Esto puede ser reescrito como:

$${\ displaystyle \ ln \, {(- \ ln {[1-Y (t)]})} = \ ln K + n \ ln t \, \!}

lo que permite la determinación de las constantes n y k a partir de una gráfica de lnln (1 / (1-Y)) vs ln (t). Si la transformación sigue la ecuación de Avrami, se obtiene una línea recta con gradiente n e intercepción en K.

Tamaño final de cristalita (dominio) [ editar ]

La cristalización ha terminado en gran parte cuando $${\ displaystyle Y} alcanza valores cercanos a 1, que estarán en un tiempo de cristalización $${\ displaystyle t_ {X}} definido por $${\ displaystyle Kt_ {X} ^ {n} \ sim 1}, como entonces el término exponencial en la expresión anterior para $${\ displaystyle Y}será pequeño Así la cristalización lleva un tiempo de orden.

$${\ displaystyle t_ {X} \ sim {\ frac {1} {\ left ({\ dot {N}} {\ dot {G}} ^ {3} \ right) ^ {1/4}}}}

es decir, la cristalización lleva un tiempo que disminuye como uno sobre la potencia de un cuarto de la velocidad de nucleación por unidad de volumen, $${\ displaystyle {\ dot {N}}}, y uno sobre los tres cuartos de potencia de la velocidad de crecimiento $${\ displaystyle {\ dot {G}}}. Los cristalitos típicos crecen durante una fracción del tiempo de cristalización.$${\ displaystyle t_ {X}}, y así tener una dimensión lineal. $${\ displaystyle {\ dot {G}} t_ {X}}o

$${\ displaystyle {\ mbox {tamaño lineal cristalino}} \ sim {\ dot {G}} t_ {X} \ sim \ left ({\ frac {\ dot {G}} {\ dot {N}}} \ right ) ^ {1/4}}

es decir, la potencia de un cuarto de la relación entre la velocidad de crecimiento y la velocidad de nucleación por unidad de volumen. Por lo tanto, el tamaño de los cristales finales solo depende de esta relación, dentro de este modelo, y como deberíamos esperar, las tasas de crecimiento rápidas y las tasas de nucleación lentas dan como resultado cristales grandes. El volumen promedio de los cristalitos es de este tamaño lineal típico en cubos.

Todo esto asume un exponente de $${\ displaystyle n = 4 \, \!}que es apropiado para la nucleación uniforme (homogénea) en tres dimensiones. Las películas delgadas, por ejemplo, pueden ser efectivamente bidimensionales, en cuyo caso si la nucleación es nuevamente uniforme, el exponente$${\ displaystyle n = 3 \, \!}, En general, para la nucleación y crecimiento uniformes, $${\ displaystyle n = D + 1 \, \!}, para $${\ displaystyle D \, \!} La dimensionalidad del espacio en el que se produce la cristalización.

Interpretación de las constantes de Avrami [ editar ]

Originalmente, se mantuvo que n tenía un valor entero entre 1 y 4 que reflejaba la naturaleza de la transformación en cuestión. En la derivación anterior, por ejemplo, se puede decir que el valor de 4 tiene contribuciones de tres dimensiones de crecimiento y una que representa una velocidad de nucleación constante. Existen derivaciones alternativas donde n tiene un valor diferente. ^[6]

Si los núcleos están preformados y, por lo tanto, todos están presentes desde el principio, la transformación solo se debe al crecimiento tridimensional de los núcleos y n tiene un valor de 3.

Una condición interesante ocurre cuando se produce una nucleación en sitios específicos (como límites de granoo impurezas) que se saturan rápidamente poco después de que comienza la transformación. Inicialmente, la nucleación puede ser aleatoria y el crecimiento sin obstáculos lleva a valores altos para n (3,4). Una vez que los sitios de nucleación se consuman, la formación de nuevas partículas cesará.

Además, si la distribución de los sitios de nucleación no es aleatoria, entonces el crecimiento puede restringirse a 1 o 2 dimensiones. La saturación del sitio puede llevar a n valores de 1, 2 o 3 para los sitios de superficie, borde y punto, respectivamente.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Beevers-Lipson tiras en el Museo de Historia de la Ciencia, Oxford , ^[1]parte de la Cristales exposición especial en 2014. Estos fueron utilizados por el Premio Nobel ganador Dorothy Hodgkin en Oxford.

Las tiras de Beevers-Lipson fueron una ayuda computacional para los primeros cristalógrafos en el cálculo de las transformadas de Fourierpara determinar la estructura de los cristales a partir de datos cristalográficos, ^[2] permitiendo la creación de modelos para moléculas complejas. ^[3] Se usaron desde la década de 1930 ^[1] hasta que las computadoras con suficiente potencia estuvieron disponibles en la década de 1960.

La técnica fue desarrollada por C. Arnold Beevers (1908–2001), ^[4] lector de cristalografía en la Universidad de Edimburgo , y Henry Lipson CBE FRS (1910–1991), profesor de Física en el Instituto de Ciencia y Ciencia de la Universidad de Manchester. tecnología . El enfoque convirtió los cálculos considerables de sumas de Fourier multidimensionales necesarias en el análisis de la cristalografía en sumas de valores unidimensionales más manejables. ^[3] Las tiras de tarjetas dobladas con números se almacenaban normalmente en dos cajas de madera, ^[5] una para senos ^[1] y otra paracosenos . Anteriormente era necesario consultar las tablas de seno / coseno, un proceso que consumía mucho tiempo. El método fue utilizado por el Premio Nobel ganador Dorothy Hodgkin OM FRS (1910-1994). ^[1] [6] La técnica todavía se usa en programas de computadora modernos.

nemático biaxial es un cristal líquido espacialmente homogéneo con tres ejes ópticos distintos. Esto debe contrastarse con un nemático simple , que tiene un único eje preferido, alrededor del cual el sistema es rotacionalmente simétrico. El grupo de simetría de un nemático biaxial es$${\ displaystyle D_ {2h}} es decir, la de un paralelepípedo derecho rectangular, que tiene 3 ortogonales $${\ displaystyle C_ {2}}Ejes y tres planos de espejo ortogonales. En un marco alineado con los ejes ópticos, el tensor del parámetro de orden de segundo rango de un nemático biaxial tiene la forma

{\ displaystyle Q = {\ begin {pmatrix} - {\ frac {1} {2}} S + T & 0 & 0 \\ 0 & - {\ frac {1} {2}} ST & 0 \\ 0 & 0 & S \\\ end {pmatrix} }}

dónde

$${\ displaystyle S} es el parámetro estándar de orden escalar nemático

$${\ displaystyle T} Una medida de la biaxialidad.

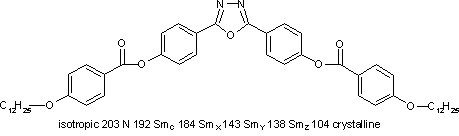
El primer informe de un nemático biaxial termotrópico apareció en 2004 ^[1] [2] basado en un mesógeno de oxadiazol de núcleo doblado en forma de boomerang . La fase nemática biaxial para este compuesto en particular solo ocurre a temperaturas alrededor de 200 ° C y está precedida por fases esmécticas aún no identificadas .

También se ha encontrado que este material puede segregarse en dominios quirales de manos opuestas. ^[3] Para que esto suceda, las moléculas en forma de boomerang adoptan una superestructura helicoidal.

En una azo doblada-core mesógeno una transición térmica se encuentra a partir de una N uniaxial _u a un biaxial nemático N _b mesofase, ^[4] según lo predicho por la teoría y la simulación. ^[5] Esta transición se observa al calentar desde la fase N _u con microscopía óptica de polarización como un cambio en la textura de Schlieren y una mayor transmitancia de la luz y desde la difracción de rayos X como la división de la reflexión nemática. La transición es una transición de segundo orden con bajo contenido de energía y, por lo tanto, no se observa en la calorimetría diferencial de barrido. El parámetro de orden posicional para la fase nemática uniaxial es de 0,75 a 1,5 veces la longitud del mesógeno y para la fase nemática biaxial 2 a 3,3 veces la longitud del mesógeno.

Otra estrategia hacia Nematics biaxial es el uso de mezclas de mesógenos en forma de varilla clásicos y en forma de disco discótico mesógenos. Se espera que la fase nemática biaxial se ubique por debajo del mínimo en el diagrama de fase de la varilla de disco. En un estudio ^[6] se encuentra realmente un sistema miscible de barras y discos, aunque la fase nemática biaxial sigue siendo difícil de alcanzar.