CRISTALOGRAFÍA

el empaquetamiento cerrado de esferas iguales es una disposición densa de esferas congruentes en una disposición infinita, regular (o enrejado ). Carl Friedrich Gauss demostró que la densidad media más alta, es decir, la fracción más grande del espacio ocupado por esferas, que puede lograrse mediante un empaque de celosía es

$${\ displaystyle {\ frac {\ pi} {3 {\ sqrt {2}}}} \ simeq 0.74048.}

La misma densidad de empaquetamiento también se puede lograr mediante apilamientos alternativos de los mismos planos de esferas empaquetados de manera cerrada, incluidas las estructuras que son aperiódicas en la dirección de apilamiento. La conjetura de Kepler afirma que esta es la densidad más alta que puede lograrse con cualquier disposición de esferas, ya sea regular o irregular. Esta conjetura fue probada por TC Hales . ^[1] [2] La densidad más alta se conoce solo en el caso de 1, 2, 3, 8 y 24 dimensiones. ^[3]

Muchas estructuras de cristal se basan en un empaquetamiento cerrado de un solo tipo de átomo, o un empaquetamiento cerrado de iones grandes con iones más pequeños que llenan los espacios entre ellos. Los arreglos cúbicos y hexagonales están muy cerca uno del otro en energía, y puede ser difícil predecir qué forma se preferirá desde los primeros principios.

Ilustración del empaquetamiento cerrado de esferas iguales en las redes hcp (izquierda) y fcc (derecha)

Celosías FCC y HCP [ editar ]

Disposición de fcc vista en dirección de eje de 4 veces

fcc		hcp
La disposición fcc puede orientarse en dos planos diferentes, cuadrado o triangular. Estos se pueden ver en el cuboctaedrocon 12 vértices que representan las posiciones de 12 esferas vecinas alrededor de una esfera central. La disposición dehcp se puede ver en la orientación triangular, pero alterna dos posiciones de esferas, en una disposición ortobicupola triangular .

Hay dos celosías regulares simples que logran esta densidad media más alta. Se llaman cara cúbica centrada ( fcc ) (también llamado cúbico cerca embalado ) y hexagonalde empaquetamiento compacto ( hcp ), en función de su simetría . Ambos se basan en láminas de esferas dispuestas en los vértices de un mosaico triangular; difieren en cómo las hojas se apilan unas sobre otras. El entramado fcc también es conocido por los matemáticos como el generado por el sistema raíz A ₃ . ^[4]

Problema bala de cañón [ editar ]

Artículo principal: Problema de bala de cañón.

Las balas de cañón apiladas en una base triangular (delantera) y rectangular (trasera) , ambas celosías de fcc .

El problema del empaquetamiento cerrado de esferas fue analizado matemáticamente por primera vez por Thomas Harriot alrededor de 1587, después de que Sir Walter Raleigh le planteara una pregunta sobre la acumulación de balas de cañón en barcos en su expedición a América. ^{[5] Las} balas de cañón generalmente se apilaban en un marco de madera rectangular o triangular, formando una pirámide de tres lados o cuatro lados. Ambas disposiciones producen una celosía cúbica centrada en la cara, con una orientación diferente al suelo. El empaquetamiento cerrado hexagonal resultaría en una pirámide de seis lados con una base hexagonal.

Bolas de nieve apiladas en preparación para una pelea de bolas de nieve . La pirámide delantera es hexagonal y la parte posterior es cúbica centrada en la cara.

El problema de la bala de cañón pregunta qué arreglos cuadrados planos de las balas de cañón se pueden apilar en una pirámide cuadrada. Édouard Lucas formuló el problema como la ecuación diofántica. $${\ displaystyle \ sum _ {n = 1} ^ {N} n ^ {2} = M ^ {2}} o $${\ displaystyle {\ frac {1} {6}} N (N + 1) (2N + 1) = M ^ {2}} y conjeturó que las únicas soluciones son $${\ displaystyle N = 1, M = 1,} y $${\ displaystyle N = 24, M = 70}. aquí$${\ displaystyle N} es el número de capas en la disposición de apilamiento piramidal y $${\ displaystyle M} es el número de balas de cañón a lo largo de un borde en el arreglo cuadrado plano.

Posicionamiento y espaciado [ editar ]

En ambos arreglos, fcc y hcp, cada esfera tiene doce vecinos. Para cada esfera hay una brecha rodeada por seis esferas (octaédricas) y dos brechas más pequeñas rodeadas por cuatro esferas (tetraédricas). Las distancias a los centros de estas brechas de los centros de las esferas que lo rodean es √ ³ / ₂ para la tetraédrica, y √ 2 para la octaédrica, cuando el radio de la esfera es 1.

Con relación a una capa de referencia con posicionamiento A, son posibles dos posicionamientos más B y C. Cada secuencia de A, B y C, sin repetición inmediata de la misma, es posible y proporciona un empaquetamiento igualmente denso para esferas de un radio determinado.

Los más regulares son

• fcc = ABC ABC ABC ... (cada tercera capa es la misma)
• hcp = AB AB AB AB ... (todas las demás capas son iguales).

Existe un número infinitamente infinito de arreglos desordenados de planos (por ejemplo, ABCACBABABAC ...) que a veces se denominan colectivamente "empaquetamientos de Barlow", después del cristalógrafo William Barlow ^[6]

En el empaquetamiento cerrado, el espaciado de centro a centro de las esferas en el plano xy es una simple teselación en forma de panal con un paso (distancia entre centros de esferas) de un diámetro de esfera. La distancia entre los centros de la esfera, proyectada en el eje z (vertical), es:

$${\ displaystyle {\ text {pitch}} _ {Z} = {\ sqrt {6}} \ cdot {d \ over 3} \ approx 0.816 \, 496 \, 58d,}

donde d es el diámetro de una esfera; esto se deduce de la disposición tetraédrica de esferas compactas.

El número de coordinación de hcp y fcc es 12 y sus factores de empaquetamiento atómico (APF) son iguales al número mencionado anteriormente, 0.74.

Comparación entre hcp y fcc
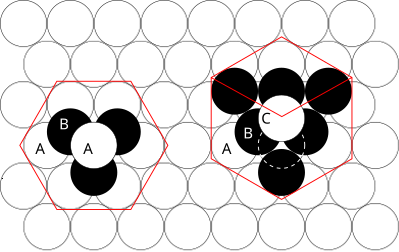Figura 1 - La red de hcp (izquierda) y la red de fcc (derecha). El contorno de cada retícula Bravais respectivase muestra en rojo. Las letras indican qué capas son iguales. Hay dos capas "A" en la matriz de hcp, donde todas las esferas están en la misma posición. Las tres capas en la pila de fcc son diferentes. Tenga en cuenta que el apilamiento de fcc se puede convertir en el apilamiento de hcp mediante la traducción de la esfera superior, como lo muestra el contorno discontinuo.

Figura 2 : aquí se muestra una pila de once esferas de la red de hcp ilustrada en la Figura 1 . La pila hcp difiere de los 3 niveles superiores de la pila fcc que se muestra en laFigura 3 solo en el nivel más bajo; se puede modificar a fcc mediante una rotación o traducción apropiada.	Figura 3 : Thomas Harriot , alrededor de 1585, primero reflexionó sobre las matemáticas de la disposición de la bala decañón o la pila de bala de cañón, que tiene una red de fcc .Observe cómo las bolas adyacentes a lo largo de cada borde del tetraedro regular que encierra la pila están en contacto directo entre sí. Esto no ocurre en una red de hcp, como se muestra en la Figura 2 .

Generación de celosía [ editar ]

Cuando se forma una red de empaquetamiento de esferas, lo primero que debe notarse es que cada vez que dos esferas tocan una línea recta, se puede dibujar desde el centro de una esfera hasta el centro de la otra intersectando el punto de contacto. La distancia entre los centros a lo largo del camino más corto es que, por lo tanto, la línea recta será r ₁  +  r _2, donde r ₁ es el radio de la primera esfera y r ₂ es el radio de la segunda. En el embalaje cerrado, todas las esferas comparten un radio común, r . Por lo tanto dos centros simplemente tendrían una distancia 2 r .

Enrejado hcp simple [ editar ]

Una animación de la generación de celosías de empaque cerrado. Nota: Si una tercera capa (no mostrada) está directamente sobre la primera capa, entonces se construye la red HCP. Si la tercera capa se coloca sobre los orificios de la primera capa, se crea la red FCC.

Para formar un empaque hexagonal de esferas ABAB -..., los puntos de coordenadas de la celosía serán los centros de las esferas. Supongamos que el objetivo es llenar una caja con esferas de acuerdo con hcp. El cuadro se colocaría en el espacio de coordenadas x - y - z .

Primero forma una fila de esferas. Los centros estarán todos en línea recta. Su coordenada x variará en 2 r ya que la distancia entre cada centro de las esferas que se tocan es 2 r . El y coordenada y y z-coordenadas será el mismo. Por simplicidad, dicen que las bolas son la primera fila y que sus Y - y Z coordenadas x son simplemente r , de manera que sus superficies se apoyan sobre las cero-planos. Las coordenadas de los centros de la primera fila serán similares a (2 r ,  r ,  r ), (4 r ,  r ,  r ), (6 r  ,r ,  r ), (8 r  , r ,  r ), ....

Ahora, forma la siguiente fila de esferas. Nuevamente, todos los centros se ubicarán en una línea recta con diferencias de coordenadas x de 2 r , pero habrá un desplazamiento de la distancia r en la dirección x, de modo que el centro de cada esfera en esta fila se alinee con la coordenada x de donde se tocan dos esferas en la primera fila. Esto permite que las esferas de la nueva fila se deslicen más cerca de la primera fila hasta que todas las esferas de la nueva fila toquen dos esferas de la primera fila. Como las nuevas esferas tocan dos esferas, sus centros forman un triángulo equilátero con los centros de esos dos vecinos. Las longitudes de los lados son todas 2 r , por lo que la altura o y-la diferencia de coordenadas entre las filas es √ 3 r . Por lo tanto, esta fila tendrá coordenadas como esta:

$${\ displaystyle \ left (r, r + {\ sqrt {3}} r, r \ right), \ \ left (3r, r + {\ sqrt {3}} r, r \ right), \ \ left (5r, r + {\ sqrt {3}} r, r \ right), \ \ left (7r, r + {\ sqrt {3}} r, r \ right), \ dots.}

La primera esfera de esta fila solo toca una esfera en la fila original, pero su ubicación se ajusta al resto de la fila.

La siguiente fila sigue este patrón de desplazamiento de la coordenada x por r y la coordenada y por √ 3 . Agregue filas hasta alcanzar los límites máximos x e y del cuadro.

En un patrón de apilamiento ABAB -..., los planos impares de esferas tendrán exactamente las mismas coordenadas, salvo una diferencia de tono en las coordenadas z, y los planos pares de esferas compartirán las mismas coordenadas x e y . Ambos tipos de planos se forman utilizando el patrón mencionado anteriormente, pero el lugar de inicio para la primera esfera de la primera fila será diferente.

Utilizando el plano descrito anteriormente como plano # 1, el plano A, coloque una esfera encima de este plano de modo que quede en contacto con tres esferas en el plano A. Las tres esferas ya se tocan entre sí, formando un triángulo equilátero, y como todas tocan la nueva esfera, los cuatro centros forman un tetraedro regular . ^[7]Todos los lados son iguales a 2 r porque todos los lados están formados por dos esferas que tocan. La altura de los cuales o la z diferencia coordenada entre los dos "planos" es √ 6 r 2/3 . Esto, combinado con las compensaciones en la x y la y.-Coordinadas da los centros de la primera fila en el plano B:

$${\ displaystyle \ left (r, r + {\ frac {{\ sqrt {3}} r} {3}}, r + {\ frac {{\ sqrt {6}} r2} {3}} \ right), \ left (3r, r + {\ frac {{\ sqrt {3}} r} {3}}, r + {\ frac {{\ sqrt {6}} r2} {3}} \ right), \ \ left ( 5r, r + {\ frac {{\ sqrt {3}} r} {3}}, r + {\ frac {{\ sqrt {6}} r2} {3}} \ right), \ \ left (7r, r + {\ frac {{\ sqrt {3}} r} {3}}, r + {\ frac {{\ sqrt {6}} r2} {3}} \ right), \ dots.}

Las coordenadas de la segunda fila siguen el patrón descrito anteriormente y son:

$${\ displaystyle \ left (2r, r + {\ frac {4 {\ sqrt {3}} r} {3}}, r + {\ frac {{\ sqrt {6}} r2} {3}} \ right), \ \ left (4r, r + {\ frac {4 {\ sqrt {3}} r} {3}}, r + {\ frac {{\ sqrt {6}} r2} {3}} \ right), \ \ izquierda (6r, r + {\ frac {4 {\ sqrt {3}} r} {3}}, r + {\ frac {{\ sqrt {6}} r2} {3}} \ derecha), \ \ izquierda ( 8r, r + {\ frac {4 {\ sqrt {3}} r} {3}}, r + {\ frac {{\ sqrt {6}} r2} {3}} \ right), \ dots.}

La diferencia con el siguiente plano, el plano A, es de nuevo √ 6 r 2/3 en el z dirección x y un cambio en la x y ypara que coincida con los x - y Y coordenadas x de la primera un avión. ^[8]

En general, las coordenadas de los centros de esfera se pueden escribir como:

$${\ displaystyle {\ begin {bmatrix} 2i + ((j \ + \ k) {\ bmod {2}}) \\ {\ sqrt {3}} \ left [j + {\ frac {1} {3}} ( k {\ bmod {2}}) \ right] \\ {\ frac {2 {\ sqrt {6}}} {3}} k \ end {bmatrix}} r}

donde i , j y k son índices que comienzan en 0 para las coordenadas x , y y z .

Índices de Miller [ editar ]

Artículo principal: Índice de Miller

Índice de Miller – Bravais para la red de hcp

Las características cristalográficas de los sistemas hcp, como los vectores y las familias de planos atómicos, se pueden describir utilizando una notación de índice de Miller de cuatro valores ( hkil ) en la que el tercer índice i denota un componente conveniente pero degenerado que es igual a - h  -  k . Las direcciones de los índices h , i y k están separadas por 120 ° y, por lo tanto, no son ortogonales; la componente les mutuamente perpendicular a las direcciones de índice h , i y k .

Rellenando el espacio restante [ editar ]

Las empaquetaduras fcc y hcp son las empaquetaduras conocidas más densas de esferas iguales con la simetría más alta (unidades de repetición más pequeñas). Se conocen empaquetamientos de esferas más densos , pero implican un empaquetamiento de esferas desigual . Una densidad de empaque de 1, llenando completamente el espacio, requiere formas no esféricas, como los panales .

Reemplazar cada punto de contacto entre dos esferas con un borde que conecta los centros de las esferas en contacto produce tetraedros y octaedros de longitudes de borde iguales. La disposición fcc produce el panal tetraédrico-octaédrico . La disposición del hcp produce el panal tetraédrico-octaédrico girado . Si, en cambio, cada esfera se incrementa con los puntos en el espacio que están más cerca de ella que de cualquier otra esfera, se producen los duales de estos panales: el panal rombal dodecaédrico para fcc y el trapecio-rómbico dodecaédrico para hcp.

Burbujas esféricas en agua jabonosa en una disposición de fcc o hcp, cuando el agua en los huecos entre las burbujas se drena, también se aproxima al nido de abeja dodecaédrico rombal o al panal de abeja dodecaédrica trapezo-rómbica . Sin embargo, tales espumas de fcc o hcp de contenido líquido muy pequeño son inestables, ya que no satisfacen las leyes de Plateau . La espuma Kelvin y la espuma Weaire-Phelan son más estables, ya que tienen una energía interfacial más pequeña en el límite de un contenido líquido muy pequeño.