CRISTALOGRAFÍA

El efecto Borrmann (o efecto Borrmann-Campbell después de Gerhard Borrmann y Herbert N. Campbell) es el aumento anómalo de la intensidad de los rayos X transmitidos a través de un cristal cuando se configura para la reflexión de Bragg .

El efecto Borrmann, un aumento dramático en la transparencia de los rayos X, se observa cuando los rayos X que satisfacen la ley de Bragg difractan a través de un cristal perfecto. La minimización de la absorción observada en el efecto Borrmann se ha explicado al observar que el campo eléctrico del haz de rayos X se acerca a una amplitud cero en los planos cristalinos, evitando así los átomos.

plano de Bragg es un plano en el espacio recíproco que biseca un vector de red recíproco,$${\ displaystyle \ scriptstyle \ mathbf {K}}, a ángulos correctos. ^[1] El plano de Bragg se define como parte de la condición Von Laue para picos de difracción en la cristalografía de difracción de rayos x .

Teniendo en cuenta el diagrama adyacente, la onda plana de rayos X que llega se define por:

$${\ displaystyle e ^ {i \ mathbf {k} \ cdot \ mathbf {r}} = \ cos {(\ mathbf {k} \ cdot \ mathbf {r})} + i \ sin {(\ mathbf {k} \ cdot \ mathbf {r})}}

Dónde $${\ displaystyle \ scriptstyle \ mathbf {k}} es el vector de onda incidente dado por:

$${\ displaystyle \ mathbf {k} = {\ frac {2 \ pi} {\ lambda}} {\ hat {n}}}

dónde $${\ displaystyle \ scriptstyle \ lambda}Es la longitud de onda del fotón incidente . Mientras que la formulación de Bragg asume una elección única de planos de celosía directos y reflexión especular de los rayos X incidentes, la fórmula de Von Laue solo supone luz monocromática y que cada centro de dispersión actúa como una fuente de ondas secundarias como lo describe el principio de Huygens . Cada onda dispersada contribuye a una nueva onda plana dada por:

$${\ displaystyle \ mathbf {k ^ {\ prime}} = {\ frac {2 \ pi} {\ lambda}} {\ hat {n}} ^ {\ prime}}

La condición para la interferencia constructiva en el $${\ displaystyle \ scriptstyle {\ hat {n}} ^ {\ prime}}la dirección es que la diferencia de trayectoria entre los fotones es un número entero (m) de su longitud de onda. Sabemos entonces que para la interferencia constructiva tenemos:

$${\ displaystyle | \ mathbf {d} | \ cos {\ theta} + | \ mathbf {d} | \ cos {\ theta ^ {\ prime}} = \ mathbf {d} \ cdot ({\ hat {n} } - {\ hat {n}} ^ {\ prime}) = m \ lambda}

dónde $${\ displaystyle \ scriptstyle m ~ \ in ~ \ mathbb {Z}}. Multiplicando lo anterior por$${\ displaystyle \ scriptstyle {\ frac {2 \ pi} {\ lambda}}} formulamos la condición en términos de los vectores de onda, $${\ displaystyle \ scriptstyle \ mathbf {k}} y $${\ displaystyle \ scriptstyle \ mathbf {k ^ {\ prime}}}:

$${\ displaystyle \ mathbf {d} \ cdot (\ mathbf {k} - \ mathbf {k ^ {\ prime}}) = 2 \ pi m}

El plano de Bragg en azul, con su vector recíproco asociado K.

Ahora considere que un cristal es un conjunto de centros de dispersión, cada uno en un punto de la red de Bravais . Podemos establecer uno de los centros de dispersión como el origen de una matriz. Dado que los puntos de la red son desplazados por los vectores de red de Bravais,$${\ displaystyle \ scriptstyle \ mathbf {R}}, las ondas dispersas interfieren constructivamente cuando la condición anterior se cumple simultáneamente para todos los valores de $${\ displaystyle \ scriptstyle \ mathbf {R}} que son vectores de celosía de Bravais, la condición se convierte en:

$${\ displaystyle \ mathbf {R} \ cdot \ left (\ mathbf {k} - \ mathbf {k ^ {\ prime}} \ right) = 2 \ pi m}

Una declaración equivalente (ver descripción matemática de la red recíproca ) es decir que:

$${\ displaystyle e ^ {i (\ mathbf {k} - \ mathbf {k ^ {\ prime}}) \ cdot \ mathbf {R}} = 1}

Al comparar esta ecuación con la definición de un vector de red recíproca, vemos que se produce una interferencia constructiva si $${\ displaystyle \ scriptstyle \ mathbf {K} ~ = ~ \ mathbf {k} \, - \, \ mathbf {k ^ {\ prime}}}Es un vector de la red recíproca. Notamos que$${\ displaystyle \ scriptstyle \ mathbf {k}} y $${\ displaystyle \ scriptstyle \ mathbf {k ^ {\ prime}}} tienen la misma magnitud, podemos afirmar que la formulación de Von Laue requiere que la punta del vector de onda incidente, $${\ displaystyle \ scriptstyle \ mathbf {k}}, debe estar en el plano que es una bisectriz perpendicular del vector de red recíproca, $${\ displaystyle \ scriptstyle \ mathbf {K}}. Este plano espacial recíproco es el plano de Bragg .

red de Bravais , llamada así por Auguste Bravais  ( 1850 ), ^[1] es una matriz infinita de puntos discretos generados por un conjunto de operaciones de traducción discretas descritas en el espacio tridimensional por:

$${\ displaystyle \ mathbf {R} = n_ {1} \ mathbf {a} _ {1} + n_ {2} \ mathbf {a} _ {2} + n_ {3} \ mathbf {a} _ {3} }

donde n _i son cualquier número entero y a _i son vectores primitivos que se encuentran en diferentes direcciones (no necesariamente mutuamente perpendiculares) y abarcan la red. Este conjunto discreto de vectores debe cerrarse bajo la suma y resta del vector. Para cualquier elección del vector de posición R , la red se ve exactamente igual.

Cuando los puntos discretos son átomos , iones o cadenas de polímero de materia sólida , el concepto de red de Bravais se utiliza para definir formalmente una disposición cristalina y sus fronteras (finitas). Un cristal se compone de una disposición periódica de uno o más átomos (la base o motivo ) que se repite en cada punto de la red. En consecuencia, el cristal tiene el mismo aspecto cuando se ve desde cualquier punto de la red equivalente, es decir, aquellos separados por la traducción de una celda unitaria.

Dos redes de Bravais a menudo se consideran equivalentes si tienen grupos de simetría isomórficos. En este sentido, hay 14 redes de Bravais posibles en el espacio tridimensional. Los 14 grupos de simetría posibles de las redes de Bravais son 14 de los 230 grupos espaciales .

En 2 dimensiones [ editar ]

Más información: Celosía (grupo)

1 - oblicua (monoclínica), 2 - rectangular (ortorrómbica), 3 centrada (ortorrómbica), 4 - hexagonal y 5 - cuadrada (tetragonal).

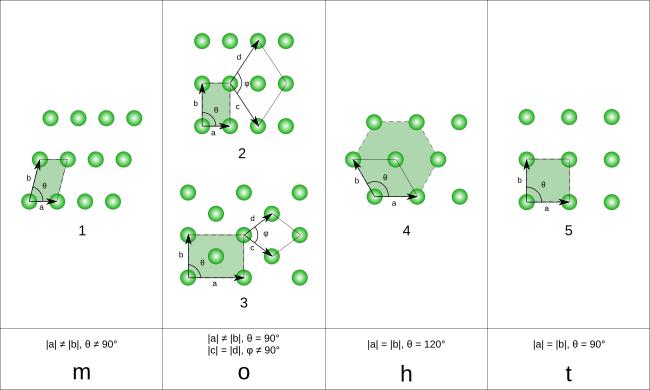
En el espacio bidimensional, hay 5 celosías Bravais, ^[2] agrupadas en cuatro familias de cristales .

Familia de cristal	Grupo de puntos  ( notación de Schönflies )	5 celosías de Bravais
		Primitivo	Centrado
Monoclínico	C 2	Oblicuo
Ortorrómbica	D 2	Rectangular	Centrada rectangular
Hexagonal	D 6	Hexagonal
Tetragonal	D 4	Cuadrado

Las celdas unitarias son especificados de acuerdo con las longitudes relativas de los bordes de células ( una y b) y el ángulo entre ellos ( θ ). El área de la celda unitaria se puede calcular evaluando la norma || a × b || , donde a y b son los vectores reticulares. Las propiedades de las familias de cristal se dan a continuación:

Familia de cristal	Zona	Distancias axiales (longitudes de borde)	Angulo axial
Monoclínico	$${\ displaystyle ab \, \ sin \ theta}	a ≠ b	θ ≠ 90 °
Ortorrómbica	$${\ displaystyle ab}	a ≠ b	θ = 90 °
Hexagonal	$${\ displaystyle {\ frac {\ sqrt {3}} {2}} \, a ^ {2}}	a = b	θ = 120 °
Tetragonal	$${\ displaystyle a ^ {2}}	a = b	θ = 90 °

En 3 dimensiones [ editar ]

Celdas unitarias de 2 × 2 × 2 de una red cúbica de diamante

En el espacio tridimensional, hay 14 celosías Bravais. Estos se obtienen combinando uno de los siete sistemas de celosía con uno de los tipos de centrado. Los tipos de centrado identifican las ubicaciones de los puntos de celosía en la celda unitaria de la siguiente manera:

• Primitivo (P): puntos de celosía solo en las esquinas de las celdas (a veces se denomina simple)
• Centrado en la base (A, B o C): puntos de celosía en las esquinas de la celda con un punto adicional en el centro de cada cara de un par de caras paralelas de la celda (a veces llamadas centradas en el extremo)
• Centrado en el cuerpo (I): puntos de celosía en las esquinas de la celda, con un punto adicional en el centro de la celda
• Centrado en la cara (F): puntos de celosía en las esquinas de la celda, con un punto adicional en el centro de cada una de las caras de la celda

No todas las combinaciones de sistemas de celosía y tipos de centrado son necesarias para describir todas las redes posibles, ya que se puede demostrar que varias de ellas son, de hecho, equivalentes entre sí. Por ejemplo, la red monoclínica I puede describirse por una red monoclínica C por diferentes opciones de ejes de cristal. De manera similar, todas las celosías centradas en A o B pueden describirse mediante un centrado en C o en P. Esto reduce el número de combinaciones a 14 celosías Bravais convencionales, como se muestra en la siguiente tabla. ^[3]

Familia de cristal	Sistema de celosía	Schönflies	14 celosías de Bravais
			Primitiva (p)	Base centrada (C)	Centrado en el cuerpo (I)	Centrado en la cara (F)
Triclínico		C i
Monoclínico		C 2h
Ortorrómbica		D 2h
Tetragonal		D 4h
Hexagonal	Romboédrica	D 3d
	Hexagonal	D 6h
Cúbico		O h

Las celdas unitarias se especifican de acuerdo con las longitudes relativas de los bordes de las celdas ( a , b , c ) y los ángulos entre ellas ( α , β , γ ). El volumen de la celda unitaria se puede calcular evaluando el producto triple a · ( b × c ) , donde a , b y c son los vectores de celosía. Las propiedades de los sistemas de celosía se dan a continuación:

Familia de cristal	Sistema de celosía	Volumen	Distancias axiales (longitudes de borde)[4]	Angulos axiales[4]	Ejemplos correspondientes
Triclínico		$${\ displaystyle abc {\ sqrt {1- \ cos ^ {2} \ alpha - \ cos ^ {2} \ beta - \ cos ^ {2} \ gamma +2 \ cos \ alpha \ cos \ beta \ cos \ gamma }}}	(Todos los casos restantes)		K 2 Cr 2 O 7 ,CuSO 4 · 5H 2 O ,H 3 BO 3
Monoclínico		$${\ displaystyle abc \, \ sin \ beta}	a ≠ c	α = γ = 90 °, β ≠ 90 °	Azufre monoclínico , Na 2SO 4 · 10H 2 O ,PbCrO 3
Ortorrómbica		$${\ displaystyle abc}	a ≠ b ≠ c	α = β = γ= 90 °	Azufre rombal ,KNO 3 , BaSO 4
Tetragonal		$${\ displaystyle a ^ {2} c}	a = b ≠ c	α = β = γ= 90 °	Lata blanca , SnO 2 , TiO 2 , CaSO 4
Hexagonal	Romboédrica	$${\ displaystyle a ^ {3} {\ sqrt {1-3 \ cos ^ {2} \ alpha +2 \ cos ^ {3} \ alpha}}}	a = b = c	α = β = γ≠ 90 °	Calcita (CaCO 3 ),cinabrio (HgS)
	Hexagonal	$${\ displaystyle {\ frac {\ sqrt {3}} {2}} \, a ^ {2} c}	a = b	α = β = 90 °, γ = 120 °	Grafito , ZnO ,CdS
Cúbico		$${\ displaystyle a ^ {3}}	a = b = c	α = β = γ= 90 °	NaCl , blenda de zinc , metal de cobre , KCl ,diamante , plata

En 4 dimensiones [ editar ]

En cuatro dimensiones, hay 64 celosías Bravais. De estos, 23 son primitivos y 41 están centrados. Diez celosías Bravais se dividen en pares enantiomórficos .