QUÍMICA - QUÍMICA ANALÍTICA

 la corriente oscura se refiere a la respuesta constante producida por un receptor espectroquímico, incluso en ausencia de radiación. Esta respuesta se agrega a la señal producida cuando el receptor se usa para medir la luz, por lo que debe tratarse para determinar qué parte de la respuesta del detector se debe realmente a la radiación. Para compensar esta señal adicional, la corriente oscura puede medirse en ausencia de radiación y luego restarse de la señal final o reducirse a cero mediante un circuito de compensación . Esto a menudo se denomina "supresión" y es una forma de corrección en blanco .

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Distribución de iones en una solución.

Los químicos Peter Debye y Erich Hückel notaron que lassoluciones que contienen solutos iónicos no se comportan idealmente incluso en concentraciones muy bajas. Entonces, mientras que la concentración de los solutos es fundamental para el cálculo de la dinámica de una solución, ellos teorizaron que un factor extra que llamaron gamma es necesario para el cálculo de los coeficientes de actividad de la solución. Por lo tanto, desarrollaron la ecuación de Debye-Hückel y la ley limitante de Debye-Hückel . La actividad es solo proporcional a la concentración y se ve alterada por un factor conocido como el coeficiente de actividad$${\ displaystyle \ gamma}. Este factor tiene en cuenta la energía de interacción de los iones en solución.

Ley de limitación de Debye – Hückel [ editar ]

Para los principios utilizados para derivar esta ecuación, consulte la teoría de Debye-Hückel .

Para calcular la actividad. $${\ displaystyle a_ {C}}de un ion C en una solución, uno debe conocer la concentración y el coeficiente de actividad:

$${\ displaystyle a_ {C} = \ gamma {\ frac {[C]} {[C ^ {\ ominus}]}},}

dónde

$${\ displaystyle \ gamma} es el coeficiente de actividad de C,

$${\ displaystyle [C ^ {\ ominus}]}es la concentración del estado estándar elegido , por ejemplo, 1 mol / kg si se usa la molalidad ,

$${\ displaystyle [C]} Es una medida de la concentración de C.

Divisor $${\ displaystyle [C]} con $${\ displaystyle [C ^ {\ ominus}]} Da una cantidad adimensional.

La ley de limitación de Debye-Hückel permite determinar el coeficiente de actividad de un ión en una solución diluida de fuerza iónica conocida . La ecuación es ^{[1] : sección 2.5.2}

$${\ displaystyle \ ln (\ gamma _ {i}) = - {\ frac {z_ {i} ^ {2} q ^ {2} \ kappa} {8 \ pi \ varepsilon _ {r} \ varepsilon _ {0 } k_ {B} T}} = - {\ frac {z_ {i} ^ {2} q ^ {3} N _ {\ text {A}} ^ {1/2}} {4 \ pi (\ varepsilon _ {r} \ varepsilon _ {0} k_ {B} T) ^ {3/2}}} {\ sqrt {10 ^ {3} {\ frac {I} {2}}}} = - Az_ {i} ^ {2} {\ sqrt {I}},}

dónde

$${\ displaystyle z_ {i}}es el número de carga de las especies de iones i ,

$${\ displaystyle q}es la carga elemental ,

$${\ displaystyle \ kappa}es la inversa de la longitud de cribado de Debye (definida a continuación),

$${\ displaystyle \ varepsilon _ {r}}es la permitividad relativa del solvente,

$${\ displaystyle \ varepsilon _ {0}}es la permitividad del espacio libre ,

$${\ displaystyle k_ {B}}es la constante de Boltzmann ,

$${\ displaystyle T}es la temperatura de la solución,

$${\ displaystyle N _ {\ mathrm {A}}}es el numero de avogadro ,

$${\ displaystyle I}es la fuerza iónica de la solución (definida a continuación),

$${\ displaystyle A}Es una constante que depende de la temperatura. Si$${\ displaystyle I} se expresa en términos de molalidad, en lugar de molaridad (como en la ecuación anterior y en el resto de este artículo), luego un valor experimental para $${\ displaystyle A} de agua es$${\ displaystyle 1.172 {\ text {mol}} ^ {- 1/2} {\ text {kg}} ^ {1/2}}a 25 ° C. Es común usar un logaritmo en base 10, en cuyo caso factorizamos$${\ displaystyle \ ln 10}, entonces A es$${\ displaystyle 0.509 {\ text {mol}} ^ {- 1/2} {\ text {kg}} ^ {1/2}}.

Es importante tener en cuenta que dado que los iones en la solución actúan juntos, el coeficiente de actividad obtenido de esta ecuación es en realidad un coeficiente de actividad promedio.

El exceso de presión osmótica obtenida de la teoría de Debye-Hückel está en unidades cgs : ^[1]

$${\ displaystyle P ^ {\ text {ex}} = - {\ frac {k_ {B} T \ kappa _ {\ text {cgs}} ^ {3}} {24 \ pi}} = - {\ frac { k_ {B} T \ left ({\ frac {4 \ pi \ sum _ {j} c_ {j} q_ {j}} {\ epsilon _ {0} \ epsilon _ {r} k_ {B} T}} \ right) ^ {3/2}} {24 \ pi}}.}

Por lo tanto, la presión total es la suma del exceso de presión osmótica y la presión ideal. $${\ displaystyle P ^ {\ text {id}} = k_ {B} T \ sum _ {i} c_ {i}}. El coeficiente osmótico es entonces dado por

$${\ displaystyle \ phi = {\ frac {P ^ {\ text {id}} + P ^ {\ text {ex}}} {P ^ {\ text {id}}}} = 1 + {\ frac {P ^ {\ text {ex}}} {P ^ {\ text {id}}}}.}

Resumen del primer artículo de Debye y Hückel sobre la teoría de los electrolitos diluidos [ editar ]

El título en inglés del artículo es "Sobre la teoría de los electrolitos. I. Depresión del punto de congelación y fenómenos relacionados". Fue publicado originalmente en 1923 en el volumen 24 de la revista en lengua alemana Physikalische Zeitschrift . Una traducción al inglés ^{[2] : 217–63} del artículo se incluye en un libro de documentos recopilados presentados a Debye por "sus alumnos, amigos y editores con motivo de su setenta cumpleaños el 24 de marzo de 1954". ^[2] : xv El artículo trata sobre el cálculo de las propiedades de las soluciones de electrolitos que no están bajo la influencia de los campos eléctricos netos, por lo que trata de la electrostática .

En el mismo año en que publicaron por primera vez este artículo, Debye y Hückel, en adelante D&H, también publicaron un artículo que cubría su caracterización inicial de soluciones bajo la influencia de campos eléctricos llamada "Sobre la teoría de los electrolitos. II. Ley de limitación de la conductividad eléctrica" , pero ese artículo subsiguiente no está (todavía) cubierto aquí.

En el siguiente resumen (hasta el momento incompleto y sin verificar), se utilizan la notación moderna y la terminología, tanto de la química como de las matemáticas, para evitar confusiones. Además, con algunas excepciones para mejorar la claridad, las subsecciones de este resumen son versiones (muy) condensadas de las mismas subsecciones del artículo original.

Introducción [ editar ]

D&H nota que la fórmula de Guldberg-Waage para especies de electrolitos en equilibrio de reacción química en forma clásica es ^[2] : 221

$${\ displaystyle \ prod _ {i = 1} ^ {s} x_ {i} ^ {\ nu _ {i}} = K,}

dónde

$${\ displaystyle \ textstyle \ prod}es una notación para la multiplicación ,

$${\ displaystyle i}es una variable ficticia que indica la especie,

$${\ displaystyle s} es el número de especies que participan en la reacción,

$${\ displaystyle x_ {i}}Es la fracción molar de las especies.$${\ displaystyle i},

$${\ displaystyle \ nu _ {i}}Es el coeficiente estequiométrico de las especies.$${\ displaystyle i},

K es la constante de equilibrio .

D&H dice que, debido a las "fuerzas electrostáticas mutuas entre los iones", es necesario modificar la ecuación de Guldberg-Waage reemplazando $${\ displaystyle K} con $${\ displaystyle \ gamma K}, dónde $${\ displaystyle \ gamma}es un coeficiente de actividad en general, no es un "especial" coeficiente de actividad (un coeficiente de actividad separada asociada a cada especie) -que es lo que se utiliza en la química moderna a partir de 2007 .

La relación entre $${\ displaystyle \ gamma} y los coeficientes de actividad especial. $${\ displaystyle \ gamma _ {i}}es ^[2] : 248

$${\ displaystyle \ log (\ gamma) = \ sum _ {i = 1} ^ {s} \ nu _ {i} \ log (\ gamma _ {i}).}

Fundamentos [ editar ]

D&H usa las entropías gratuitas de Helmholtz y Gibbs $${\ displaystyle \ Phi} y $${\ displaystyle \ Xi}para expresar el efecto de las fuerzas electrostáticas en un electrolito en su estado termodinámico. Específicamente, dividen la mayoría de los potenciales termodinámicos en términos clásicos y electrostáticos:

$${\ displaystyle \ Phi = S - {\ frac {U} {T}} = - {\ frac {A} {T}}

dónde

$${\ displaystyle \ Phi}es Helmholtz entropía libre ,

$${\ displaystyle S}es la entropía ,

$${\ displaystyle U}es energía interna ,

$${\ displaystyle T}es la temperatura ,

$${\ displaystyle A}Es la energía libre de Helmholtz .

D&H da el diferencial total de$${\ displaystyle \ Phi}como ^[2] : 222

$${\ displaystyle d \ Phi = {\ frac {P} {T}} \, dV + {\ frac {U} {T ^ {2}}} \, dT,}

dónde

$${\ displaystyle P}es la presión ,

$${\ displaystyle V}es volumen .

Por la definición del diferencial total, esto significa que

$${\ displaystyle {\ frac {P} {T}} = {\ frac {\ partial \ Phi} {\ partial V}},}

$${\ displaystyle {\ frac {U} {T ^ {2}}} = {\ frac {\ partial \ Phi} {\ partial T}},}

que son útiles más adelante.

Como se dijo anteriormente, la energía interna se divide en dos partes: ^[2] : 222

$${\ displaystyle U = U_ {k} + U_ {e}}

dónde

$${\ displaystyle k} indica la parte clásica,

$${\ displaystyle e} Indica la parte eléctrica.

Del mismo modo, la entropía libre de Helmholtz también se divide en dos partes:

$${\ displaystyle \ Phi = \ Phi _ {k} + \ Phi _ {e}.}

D&H declara, sin dar la lógica, que ^[2] : 222

$${\ displaystyle \ Phi _ {e} = \ int {\ frac {U_ {e}} {T ^ {2}}} \, dT.}

Parecería que, sin alguna justificación,

$${\ displaystyle \ Phi _ {e} = \ int {\ frac {P_ {e}} {T}} \, dV + \ int {\ frac {U_ {e}} {T ^ {2}}} \, dT .}

Sin mencionar específicamente, D&H luego da lo que podría ser la justificación requerida (arriba) mientras argumenta que $${\ displaystyle \ Phi _ {e} = \ Xi _ {e}}, una suposición de que el solvente es incompresible.

La definición de la entropía libre de Gibbs. $${\ displaystyle \ Xi}es ^{[2] : 222-3}

$${\ displaystyle \ Xi = S - {\ frac {U + PV} {T}} = \ Phi - {\ frac {PV} {T}} = - {\ frac {G} {T}},}

dónde $${\ displaystyle G}Es la energía libre de Gibbs .

D&H da el diferencial total de $${\ displaystyle \ Xi}como ^[2] : 222

$${\ displaystyle d \ Xi = - {\ frac {V} {T}} \, dP + {\ frac {U + PV} {T ^ {2}}} \, dT.}

En este punto, D&H nota que, para el agua que contiene 1 mol por litro de cloruro de potasio (no se dan la presión nominal y la temperatura), la presión eléctrica$${\ displaystyle P_ {e}}asciende a 20 atmósferas. Además, señalan que este nivel de presión da un cambio de volumen relativo de 0.001. Por lo tanto, descuidan el cambio en el volumen de agua debido a la presión eléctrica, escribiendo ^[2] : 223

$${\ displaystyle \ Xi = \ Xi _ {k} + \ Xi _ {e},}

y pon

$${\ displaystyle \ Xi _ {e} = \ Phi _ {e} = \ int {\ frac {U_ {e}} {T ^ {2}}} \, dT.}

D&H dice que, según Planck, la parte clásica de la entropía libre de Gibbs es ^[2] : 223

$${\ displaystyle \ Xi _ {k} = \ sum _ {i = 0} ^ {s} N_ {i} (\ xi _ {i} -k_ {B} ln (x_ {i})),}

dónde

$${\ displaystyle i} es una especie,

$${\ displaystyle s} es el número de diferentes tipos de partículas en solución,

$${\ displaystyle N_ {i}}es el numero de particulas de la especie i ,

$${\ displaystyle \ xi _ {i}}es la partícula libre de Gibbs, entropía libre de la especie i ,

$${\ displaystyle k_ {B}}es la constante de Boltzmann ,

$${\ displaystyle x_ {i}}Es la fracción molar de la especie i .

La especie cero es el solvente. La definición de$${\ displaystyle \ xi _ {i}}es como sigue, donde las letras minúsculas indican las versiones específicas de partículas de las propiedades extensivas correspondientes: ^[2] : 223

$${\ displaystyle \ xi _ {i} = s_ {i} - {\ frac {u_ {i} + Pv_ {i}} {T}}.

D&H no lo dice, pero la forma funcional de $${\ displaystyle \ Xi _ {k}}se puede derivar de la dependencia funcional del potencial químico de un componente de una mezcla ideal sobre su fracción molar. ^[3]

D&H nota que la energía interna $${\ displaystyle U}de una solución se reduce por la interacción eléctrica de sus iones, pero este efecto no se puede determinar utilizando la aproximación cristalográfica para distancias entre átomos diferentes (la raíz cúbica de la relación del volumen total al número de partículas en el volumen). ). Esto se debe a que hay más movimiento térmico en una solución líquida que en un cristal. El movimiento térmico tiende a manchar la red natural que de otro modo serían construidas por los iones. En cambio, D&H introduce el concepto de una atmósfera o nube iónica . Al igual que la red cristalina, cada ion aún intenta rodearse de iones de carga opuesta, pero de una forma más libre; a pequeñas distancias de los iones positivos, es más probable que uno encuentre iones negativos y viceversa. ^[2] : 225

La energía potencial de una solución de ion arbitrario [ editar ]

La electroneutralidad de una solución requiere que ^[2] : 233

$${\ displaystyle \ sum _ {i = 1} ^ {s} N_ {i} z_ {i} = 0,}

dónde

$${\ displaystyle N_ {i}}es el número total de iones de la especie i en la solución,

$${\ displaystyle z_ {i}}es el número de carga de la especie i .

Para llevar un ion de la especie i , inicialmente lejos, a un punto$${\ displaystyle P}dentro de la nube de iones requiere energía de interacción en la cantidad de$${\ displaystyle z_ {i} q \ varphi}, dónde $${\ displaystyle q}es la carga elemental , y$${\ displaystyle \ varphi}es el valor del campo de potencial eléctricoescalar en$${\ displaystyle P}. Si las fuerzas eléctricas fueran el único factor en el juego, la configuración de energía mínima de todos los iones se lograría en una configuración de celosía cerrada. Sin embargo, los iones están en equilibrio térmico entre sí y son relativamente libres para moverse. Así, obedecen las estadísticas de Boltzmann y forman una distribución de Boltzmann . Densidades numéricas de todas las especies. $${\ displaystyle n_ {i}} se alteran de sus valores en masa (promedio general) $${\ displaystyle n_ {i} ^ {0}}por el correspondiente factor de Boltzmann $${\ displaystyle e ^ {- {\ frac {z_ {i} q \ varphi} {k_ {B} T}}}}, dónde $${\ displaystyle k_ {B}}es la constante de Boltzmann , y$${\ displaystyle T}es la temperatura ^[4] Así, en cada punto de la nube ^[2] : 233

$${\ displaystyle n_ {i} = {\ frac {N_ {i}} {V}} e ^ {- {\ frac {z_ {i} q \ varphi} {k_ {B} T}}} = n_ {i } ^ {0} e ^ {- {\ frac {z_ {i} q \ varphi} {k_ {B} T}}}.}

Tenga en cuenta que en el límite de temperatura infinita, todos los iones se distribuyen de manera uniforme, sin tener en cuenta sus interacciones electrostáticas. ^[2] : 227

La densidad de carga está relacionada con la densidad numérica: ^[2] : 233

$${\ displaystyle \ rho = \ sum _ {i} z_ {i} qn_ {i} = \ sum _ {i} z_ {i} qn_ {i} ^ {0} e ^ {- {\ frac {z_ {i } q \ varphi} {k_ {B} T}}}.}

Al combinar este resultado para la densidad de carga con la ecuación de Poisson de electrostática, se obtiene una forma de la ecuación de Poisson-Boltzmann : ^[2] : 233

$${\ displaystyle \ nabla ^ {2} \ varphi = - {\ frac {\ rho} {\ varepsilon _ {r} \ varepsilon _ {0}}} = - \ sum _ {i} {\ frac {z_ {i } qn_ {i} ^ {0}} {\ varepsilon _ {r} \ varepsilon _ {0}}} e ^ {- {\ frac {z_ {i} q \ varphi} {k_ {B} T}}} .}

Esta ecuación es difícil de resolver y no sigue el principio de superposición lineal para la relación entre el número de cargas y la fuerza del campo potencial. Ha sido resuelto por el matemático sueco Thomas Hakon Gronwall y sus colaboradores físicos físicos V. K. La Mer y Karl Sandved en un artículo de Physikalische Zeitschrift de 1928 que trata sobre las extensiones a la teoría de Debye-Huckel, que recurrió a la expansión de la serie Taylor.

Sin embargo, para concentraciones de iones suficientemente bajas, se puede usar una aproximación de expansión de la serie de Taylor de primer orden para la función exponencial ($${\ displaystyle e ^ {x} \ approx 1 + x} para {\ displaystyle 0 ) para crear una ecuación diferencial lineal (Hamann, Hamnett y Vielstich. Electroquímica. Wiley-VCH, sección 2.4.2). D&H dice que esta aproximación se mantiene a grandes distancias entre los iones, ^[2] : 227, que es lo mismo que decir que la concentración es baja. Por último, afirman sin pruebas que la adición de más términos en la expansión tiene poco efecto en la solución final. ^[2] : 227 Así

$${\ displaystyle - \ sum _ {i} {\ frac {z_ {i} qn_ {i} ^ {0}} {\ varepsilon _ {r} \ varepsilon _ {0}}} e ^ {- {\ frac { z_ {i} q \ varphi} {k_ {B} T}}} \ approx - \ sum _ {i} {\ frac {z_ {i} qn_ {i} ^ {0}} {\ varepsilon _ {r} \ varepsilon _ {0}}} \ left (1 - {\ frac {z_ {i} q \ varphi} {k_ {B} T}} \ right) = - \ left (\ sum _ {i} {\ frac {z_ {i} qn_ {i} ^ {0}} {\ varepsilon _ {r} \ varepsilon _ {0}}} - \ sum _ {i} {\ frac {z_ {i} ^ {2} q ^ {2} n_ {i} ^ {0} \ varphi} {\ varepsilon _ {r} \ varepsilon _ {0} k_ {B} T}} \ right).

La ecuación de Poisson-Boltzmann se transforma a ^[2] : 233

$${\ displaystyle \ nabla ^ {2} \ varphi = \ sum _ {i} {\ frac {z_ {i} ^ {2} q ^ {2} n_ {i} ^ {0} \ varphi} {\ varepsilon _ {r} \ varepsilon _ {0} k_ {B} T}},}

porque la primera suma es cero debido a la electroneutralidad. ^[2] : 234

Factorice el potencial escalar y asigne las sobras, que son constantes, a $${\ displaystyle \ kappa ^ {2}}. Además, vamos$${\ displaystyle I}ser la fuerza iónicade la solución: ^[2] : 234

$${\ displaystyle \ kappa ^ {2} = \ sum _ {i} {\ frac {z_ {i} ^ {2} q ^ {2} n_ {i} ^ {0}} {\ varepsilon _ {r} \ varepsilon _ {0} k_ {B} T}} = {\ frac {2Iq ^ {2}} {\ varepsilon _ {r} \ varepsilon _ {0} k_ {B} T}},}

$${\ displaystyle I = {\ frac {1} {2}} \ sum _ {i} z_ {i} ^ {2} n_ {i} ^ {0}.}

Entonces, la ecuación fundamental se reduce a una forma de la ecuación de Helmholtz : ^[5]

$${\ displaystyle \ nabla ^ {2} \ varphi = \ kappa ^ {2} \ varphi.}

Hoy, $${\ displaystyle \ kappa ^ {- 1}}Se llama la longitud de cribado Debye . D&H reconoce la importancia del parámetro en su artículo y lo caracteriza como una medida del espesor de la atmósfera de iones, que es una doble capa eléctrica del tipo Guoy-Chapman. ^[2] : 229

La ecuación se puede expresar en coordenadas esféricas tomando$${\ displaystyle r = 0}en algún ion arbitrario: ^{[6] [2] : 229}

$${\ displaystyle \ nabla ^ {2} \ varphi = {\ frac {1} {r ^ {2}}} {\ frac {\ partial} {\ partial r}} \ left (r ^ {2} {\ frac {\ partial \ varphi (r)} {\ partial r}} \ right) = {\ frac {\ partial ^ {2} \ varphi (r)} {\ partial r ^ {2}}} + {\ frac { 2} {r}} {\ frac {\ partial \ varphi (r)} {\ partial r}} = \ kappa ^ {2} \ varphi (r).}

La ecuación tiene la siguiente solución general (tenga en cuenta que $${\ displaystyle \ kappa}es una constante positiva): ^[2] : 229

$${\ displaystyle \ varphi (r) = A {\ frac {e ^ {- {\ sqrt {\ kappa ^ {2}}} r}} {r}} + A '{\ frac {e ^ {{\ sqrt {\ kappa ^ {2}}} r}} {2r {\ sqrt {\ kappa ^ {2}}}}} = A {\ frac {e ^ {- \ kappa r}} {r}} + A ' '{\ frac {e ^ {\ kappa r}} {r}} = A {\ frac {e ^ {- \ kappa r}} {r}},}

dónde $${\ displaystyle A}, $${\ displaystyle A '}y $${\ displaystyle A ''} son constantes indeterminadas

El potencial eléctrico es cero en el infinito por definición, por lo que $${\ displaystyle A ''}debe ser cero ^[2] : 229

En el siguiente paso, D&H asume que hay un cierto radio $${\ displaystyle a_ {i}}, más allá de la cual no hay iones en la atmósfera que puedan acercarse al centro (de carga) del ión aislado. Este radio puede deberse al tamaño físico del ión en sí, a los tamaños de los iones en la nube y a las moléculas de agua que rodean a los iones. Matemáticamente, tratan el ión singular como una carga puntual a la que uno no puede acercarse dentro del radio$${\ displaystyle a_ {i}}. ^[2] : 231

El potencial de una carga puntual por sí mismo es

$${\ displaystyle \ varphi _ {\ text {pc}} (r) = {\ frac {1} {4 \ pi \ varepsilon _ {r} \ varepsilon _ {0}}} {\ frac {z_ {i} q } {r}}.}

D&H dice que el potencial total dentro de la esfera es ^[2] : 232

$${\ displaystyle \ varphi _ {\ text {sp}} (r) = \ varphi _ {\ text {pc}} (r) + B_ {i} = {\ frac {1} {4 \ pi \ varepsilon _ { r} \ varepsilon _ {0}}} {\ frac {z_ {i} q} {r}} + B_ {i},}

dónde $${\ displaystyle B_ {i}}Es una constante que representa el potencial agregado por la atmósfera iónica. No hay justificación para$${\ displaystyle B_ {i}}Se da una constante. Sin embargo, se puede ver que este es el caso al considerar que cualquier distribución de carga estática esférica está sujeta a las matemáticas del teorema de shell . El teorema de shell dice que no se ejerce ninguna fuerza sobre las partículas cargadas dentro de una esfera (de carga arbitraria). ^[7]Dado que se asume que la atmósfera de ión es esférica (promediada en el tiempo), con carga variable en función del radio$${\ displaystyle r}, puede ser representado como una serie infinita de carcasas de carga concéntricas. Por lo tanto, dentro del radio.$${\ displaystyle a_ {i}}, la atmósfera de iones no ejerce ninguna fuerza. Si la fuerza es cero, entonces el potencial es una constante (por definición).

En una combinación del modelo de distribución continua que dio la ecuación de Poisson-Boltzmann y el modelo de la carga puntual, se supone que en el radio $${\ displaystyle a_ {i}}, hay una continuidad de $${\ displaystyle \ varphi (r)}y su primer derivado. Así ^[2] : 232

$${\ displaystyle \ varphi (a_ {i}) = A_ {i} {\ frac {e ^ {- \ kappa a_ {i}}} {a_ {i}}} = {\ frac {1} {4 \ pi \ varepsilon _ {r} \ varepsilon _ {0}}} {\ frac {z_ {i} q} {a_ {i}}} + B_ {i} = \ varphi _ {\ text {sp}} (a_ { yo}),}

$${\ displaystyle \ varphi '(a_ {i}) = - {\ frac {A_ {i} e ^ {- \ kappa a_ {i}} (1+ \ kappa a_ {i})} {a_ {i} ^ {2}}} = - {\ frac {1} {4 \ pi \ varepsilon _ {r} \ varepsilon _ {0}}} {\ frac {z_ {i} q} {a_ {i} ^ {2} }} = \ varphi _ {\ text {sp}} '(a_ {i}),}

$${\ displaystyle A_ {i} = {\ frac {z_ {i} q} {4 \ pi \ varepsilon _ {r} \ varepsilon _ {0}}} {\ frac {e ^ {\ kappa a_ {i}} } {1+ \ kappa a_ {i}}},}

$${\ displaystyle B_ {i} = - {\ frac {z_ {i} q \ kappa} {4 \ pi \ varepsilon _ {r} \ varepsilon _ {0}}} {\ frac {1} {1+ \ kappa ai}}}.}

Según la definición de energía potencial eléctrica , la energía potencial asociada con el ion individualizado en la atmósfera de iones es ^{[2] : 230 y 232}

$${\ displaystyle u_ {i} = z_ {i} qB_ {i} = - {\ frac {z_ {i} ^ {2} q ^ {2} \ kappa} {4 \ pi \ varepsilon _ {r} \ varepsilon _ {0}}} {\ frac {1} {1+ \ kappa a_ {i}}}.}

Tenga en cuenta que esto solo requiere el conocimiento de la carga del ión singular y el potencial de todos los demás iones.

Para calcular la energía potencial de toda la solución de electrolito, se debe usar la generalización de carga múltiple para energía potencial eléctrica: ^{[2] : 230 y 232}

$${\ displaystyle U_ {e} = {\ frac {1} {2}} \ sum _ {i = 1} ^ {s} N_ {i} u_ {i} = - \ sum _ {i = 1} ^ { s} {\ frac {N_ {i} z_ {i} ^ {2}} {2}} {\ frac {q ^ {2} \ kappa} {4 \ pi \ varepsilon _ {r} \ varepsilon _ {0 }}} {\ frac {1} {1+ \ kappa a_ {i}}}.}

El término eléctrico adicional al potencial termodinámico [ editar ]

A este artículo le falta información sobre aún no ha sido agregado . Por favor amplíe el artículo para incluir esta información. Más detalles pueden existir en la página de discusión . ( Mayo 2018 )

Nondimensionalization [ editar ]

La exactitud fáctica de este artículo se disputa . Discusión relevante se puede encontrar en la página de discusión . Por favor, ayude a garantizar que las declaraciones en disputa se obtengan de manera confiable . ( Mayo de 2018 ) ( Aprenda cómo y cuándo eliminar este mensaje de plantilla )

Esta sección se creó sin hacer referencia al papel original y contiene algunos errores (por ejemplo, la fuerza iónica está desactivada por un factor de dos). Una vez que se hayan rectificado, esta sección probablemente debería moverse al artículo de no dimensionalización y luego vincularse desde aquí, ya que la versión no dimensional de la ecuación de Poisson-Boltzmann no es necesaria para entender la teoría D&H.

La ecuación diferencial está lista para la solución (como se indicó anteriormente, la ecuación solo se aplica a concentraciones bajas):

$${\ displaystyle {\ frac {\ parcial ^ {2} \ varphi (r)} {\ parcial r ^ {2}}} + {\ frac {2} {r}} {\ frac {\ parcial \ varphi (r )} {\ partial r}} = {\ frac {Iq \ varphi (r)} {\ varepsilon _ {r} \ varepsilon _ {0} k_ {b} T}} = \ kappa ^ {2} \ varphi ( r).

El uso del teorema π de Buckingham en este problema da como resultado los siguientes grupos adimensionales:

$${\ displaystyle \ pi _ {1} = {\ frac {q \ varphi (r)} {k_ {b} T}} = \ Phi (R (r))}

$${\ displaystyle \ pi _ {2} = \ varepsilon _ {r}}

$${\ displaystyle \ pi _ {3} = {\ frac {ak_ {b} T \ varepsilon _ {0}} {q ^ {2}}}}

$${\ displaystyle \ pi _ {4} = a ^ {3} I}

$${\ displaystyle \ pi _ {5} = z_ {0}}

$${\ displaystyle \ pi _ {6} = {\ frac {r} {a}} = R (r).}

$${\ displaystyle \ Phi} Se llama campo de potencial eléctrico escalar reducido. $${\ displaystyle R}Se llama el radio reducido. Los grupos existentes pueden recombinarse para formar otros dos grupos adimensionales para la sustitución en la ecuación diferencial. El primero es lo que podría llamarse el cuadrado de la longitud de cribado inversa reducida ,$${\ displaystyle (\ kappa a) ^ {2}}. El segundo podría llamarse la carga central reducida de iones,$${\ displaystyle Z_ {0}}(con una Z mayúscula). Tenga en cuenta que, sin embargo$${\ displaystyle z_ {0}} Ya no tiene dimensiones, sin la sustitución que se da a continuación, la ecuación diferencial aún sería dimensional.

$${\ displaystyle {\ frac {\ pi _ {4}} {\ pi _ {2} \ pi _ {3}}} = {\ frac {a ^ {2} q ^ {2} I} {\ varepsilon _ {r} \ varepsilon _ {0} k_ {b} T}} = (\ kappa a) ^ {2}}

$${\ displaystyle {\ frac {\ pi _ {5}} {\ pi _ {2} \ pi _ {3}}} = {\ frac {z_ {0} q ^ {2}} {4 \ pi a \ varepsilon _ {r} \ varepsilon _ {0} k_ {b} T}} = Z_ {0}}

Para obtener la ecuación diferencial no dimensionalizada y las condiciones iniciales, use la $${\ displaystyle \ pi} grupos para eliminar $${\ displaystyle \ varphi (r)} a favor de $${\ displaystyle \ Phi (R (r))}, luego eliminar $${\ displaystyle R (r)} a favor de $${\ displaystyle r} Mientras se lleva a cabo la regla de la cadena y la sustitución. $${\ displaystyle {R ^ {\ prime}} (r) = a}, luego eliminar $${\ displaystyle r} a favor de $${\ displaystyle R} (no se necesita una regla de la cadena), luego elimine $${\ displaystyle I} a favor de $${\ displaystyle (\ kappa a) ^ {2}}, luego eliminar $${\ displaystyle z_ {0}} a favor de $${\ displaystyle Z_ {0}}. Las ecuaciones resultantes son las siguientes:

$${\ displaystyle {\ frac {\ partial \ Phi (R)} {\ partial R}} {\ bigg |} _ {R = 1} = - Z_ {0}}

$${\ displaystyle \ Phi (\ infty) = 0}

$${\ displaystyle {\ frac {\ parcial ^ {2} \ Phi (R)} {\ parcial R ^ {2}}} + {\ frac {2} {R}} {\ frac {\ parcial \ Phi (R )} {\ partial R}} = (\ kappa a) ^ {2} \ Phi (R).}

Para la sal de mesa en una solución 0.01 M a 25 ° C, un valor típico de $${\ displaystyle (\ kappa a) ^ {2}} es 0.0005636, mientras que un valor típico de $${\ displaystyle Z_ {0}} es 7.017, destacando el hecho de que, en bajas concentraciones, $${\ displaystyle (\ kappa a) ^ {2}}es un objetivo para un orden de magnitud cero de aproximación, como el análisis de perturbaciones. Desafortunadamente, debido a la condición límite en el infinito, la perturbación regular no funciona. La misma condición límite nos impide encontrar la solución exacta a las ecuaciones. Sin embargo, la perturbación singular puede funcionar.

La verificación experimental de la teoría [ editar ]

Para verificar la validez de la teoría de Debye-Hückel, se han probado muchas formas experimentales, midiendo los coeficientes de actividad: el problema es que tenemos que ir hacia diluciones muy altas. Ejemplos típicos son: mediciones de presión de vapor, punto de congelación, presión osmótica (métodos indirectos) y medición de potencial eléctrico en células (método directo). En cuanto a las diluciones elevadas, se han encontrado buenos resultados con células de membrana líquida, ha sido posible investigar medios acuosos 10 ⁻⁴M y se ha encontrado que para los electrolitos 1: 1 (como NaCl o KCl) la ecuación de Debye-Hückel es totalmente correcta, pero para los electrolitos 2: 2 o 3: 2 es posible encontrar una desviación negativa del límite de Debye-Hückel ley: este comportamiento extraño se puede observar solo en el área muy diluida, y en regiones más concentradas la desviación se vuelve positiva. Es posible que la ecuación de Debye-Hückel no sea capaz de prever este comportamiento debido a la linealización de la ecuación de Poisson-Boltzmann, o tal vez no: los estudios sobre esto se han iniciado solo durante los últimos años del siglo XX porque antes no estaba Es posible investigar la región 10 ⁻⁴ M, por lo que es posible que durante los próximos años nazcan nuevas teorías.

Extensiones de la teoría [ editar ]

Advertencia: la notación en esta sección es (actualmente) diferente a la del resto del artículo.

Se han propuesto una serie de enfoques para extender la validez de la ley a los rangos de concentración que se encuentran comúnmente en la química

Una de estas ecuaciones de Debye-Hückel es dada por:

$${\ displaystyle \ - \ log _ {10} (\ gamma) = {\ frac {A | z _ {+} z _ {-} | {\ sqrt {I}}} {1 + Ba {\ sqrt {I}} }} \,}

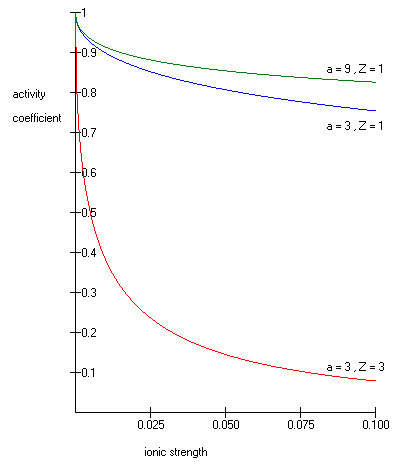
dónde $${\ displaystyle \ \ gamma \,}como su logaritmo común es el coeficiente de actividad,$${\ displaystyle \ z \,}es la carga entera del ión (1 para H ⁺ , 2 para Mg ^2+, etc.),$${\ displaystyle \ I \,} es la fuerza iónica de la solución acuosa, y $${\ displaystyle \ a \,}es el tamaño o diámetro efectivo del ion en angstrom . El radio hidratado efectivo del ion, a, es el radio del ion y sus moléculas de agua estrechamente unidas. Los iones grandes y los iones menos altamente cargados se unen al agua con menos fuerza y ​​tienen radios hidratados más pequeños que los iones más pequeños y con mayor carga. Los valores típicos son 3Å para iones como H ⁺ , Cl ^- , CN ^- y HCOO ^- . El diámetro efectivo para el ion hidronio es 9Å.$${\ displaystyle \ A \,} y $${\ displaystyle \ B \,}son constantes con valores de 0.5085 y 0.3281 respectivamente a 25 ° C en agua ^[2] .

La ecuación extendida de Debye-Hückel proporciona resultados precisos para μ ≤ 0.1. Para soluciones de mayor fuerza iónica, se deben usar las ecuaciones de Pitzer . En estas soluciones, el coeficiente de actividad puede aumentar con la fuerza iónica.

La ecuación de Debye-Hückel no se puede usar en soluciones de surfactantes donde la presencia de micelasinfluye en las propiedades electroquímicas del sistema (incluso un juicio aproximado sobreestima a γ en ~ 50%).