TERMODINÁMICA

El enfriamiento por evaporación es una técnica de física atómica para lograr altas densidades de espacio de fase que las técnicas de enfriamiento óptico normalmente no pueden alcanzar. ^[1]

Los átomos atrapados en trampas ópticas o magnéticas se enfrían a medida que la profundidad de la trampa disminuye y los átomos más calientes (con la energía cinética más alta) abandonan la trampa. Los átomos calientes que salen de la trampa están en la cola de la distribución de Maxwell-Boltzmann y, por lo tanto, eliminan una cantidad significativa de energía cinética, mitigando la pérdida de átomos por un aumento general en la densidad del espacio de fase. La técnica es análoga a enfriar una taza de café caliente soplando sobre ella.

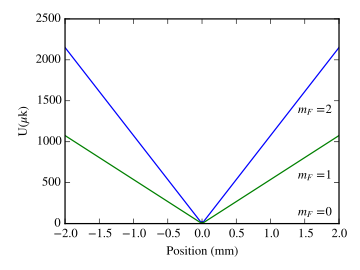
A menudo (RF radiofrecuencia radiación) se utiliza para conducir los átomos más calientes de la trampa. ^[2] La radiación de RF se conoce comúnmente como una cuchilla de RF, porque corta los átomos más calientes de la trampa.

Historia [ editar ]

El enfriamiento evaporativo se desarrolló para estudiar el condensado de Bose-Einstein , un estado exótico de la materia en el que múltiples átomos entran en el mismo estado cuántico . Esta condensación solo ocurre a temperaturas muy bajas: alrededor de 170 nanokelvinas para los átomos de rubidio .

El uso de la evaporación cinética fue pionero en 1995, primero por Eric A. Cornell y Carl Wieman para el rubidio , y luego por el grupo de Randall G. Hulet para el litio . Desde entonces, la técnica ha sido mejorada, especialmente por el equipo de Bouyer en el Groupe d'Optique Atomique Laboratoire en el Instituto de Óptica Charles Fabry .

es exacta o perfecta , en contraste con un diferencial inexacta , si se trata de la forma dQ , por alguna función diferenciable  Q .

Descripción general [ editar ]

Definición [ editar ]

Trabajamos en tres dimensiones, con definiciones similares en cualquier otro número de dimensiones. En tres dimensiones, una forma del tipo.

$${\ displaystyle A (x, y, z) \, dx + B (x, y, z) \, dy + C (x, y, z) \, dz}

Se llama una forma diferencial . Este formulario se llama exacto en un dominio$${\ displaystyle D \ subconjunto \ mathbb {R} ^ {3}}en el espacio si existe alguna función escalar $${\ displaystyle Q = Q (x, y, z)} definido en $${\ displaystyle D} tal que

$${\ displaystyle dQ \ equiv \ left ({\ frac {\ parcial Q} {\ parcial x}} \ derecha) _ {y, z} \, dx + \ izquierda ({\ frac {\ parcial Q} {\ parcial y }} \ derecha) _ {x, z} \, dy + \ izquierda ({\ frac {\ parcial Q} {\ parcial z}} \ derecha) _ {x, y} \, dz,}   $${\ displaystyle dQ = A \, dx + B \, dy + C \, dz}

a lo largo de D. Esto es equivalente a decir que el campo vectorial $${\ displaystyle (A, B, C)}Es un campo vectorial conservador, con potencial correspondiente.$${\ displaystyle Q}.

Nota: Los subíndices fuera del paréntesis indican qué variables se mantienen constantes durante la diferenciación. Debido a la definición de la derivada parcial , estos subíndices no son necesarios, pero se incluyen como un recordatorio.

Una dimensión [ editar ]

En una dimensión, una forma diferencial.

$${\ displaystyle A (x) \, dx}

es exacto siempre y cuando $${\ displaystyle A}tiene una antiderivada (pero no necesariamente una en términos de funciones elementales). Si$${\ displaystyle A} tiene una antiderivada, deja $${\ displaystyle Q} ser una antiderivada de $${\ displaystyle A} y esto $${\ displaystyle Q}Satisface la condición de exactitud. Si$${\ displaystyle A}no no tienen una primitiva, no podemos escribir$${\ displaystyle dQ = A (x) \, dx} Y así, la forma diferencial es inexacta.

Dos y tres dimensiones [ editar ]

Por simetría de segundas derivadas , para cualquier función "agradable" (no patológica )$${\ displaystyle Q} tenemos

$${\ displaystyle {\ frac {\ parcial ^ {2} Q} {\ parcial x \, \ parcial y}} = {\ frac {\ parcial ^ {2} Q} {\ parcial y \, \ parcial x}} }

Por lo tanto, se deduce que en una región R simplemente conectada del plano xy , un diferencial

$${\ displaystyle A (x, y) \, dx + B (x, y) \, dy}

Es un diferencial exacto si y solo si se cumple lo siguiente:

$${\ displaystyle \ left ({\ frac {\ parcial A} {\ parcial y}} \ derecha) _ {x} = \ izquierda ({\ frac {\ parcial B} {\ parcial x}} \ derecha) _ { y}}

Para tres dimensiones, un diferencial.

$${\ displaystyle dQ = A (x, y, z) \, dx + B (x, y, z) \, dy + C (x, y, z) \, dz}

es un diferencial exacto en una región R simplemente conectada del sistema de coordenadas xyz si entre las funciones A , B y C existen las relaciones:

$${\ displaystyle \ left ({\ frac {\ parcial A} {\ parcial y}} \ derecha) _ {x, z} \! \! \! = \ izquierda ({\ frac {\ parcial B} {\ parcial x}} \ derecha) _ {y, z}}   ;   $${\ displaystyle \ left ({\ frac {\ parcial A} {\ parcial z}} \ derecha) _ {x, y} \! \! \! = \ izquierda ({\ frac {\ parcial C} {\ parcial x}} \ derecha) _ {y, z}}   ;   $${\ displaystyle \ left ({\ frac {\ partial B} {\ partial z}} \ right) _ {x, y} \! \! \! = \ left ({\ frac {\ partial C} {\ partial y}} \ derecha) _ {x, z}}

Estas condiciones son equivalentes a las siguientes: Si G es la gráfica de esta función con valores vectoriales, para todos los vectores tangentes X , Y de la superficie G, entonces s ( X ,  Y ) = 0 con s en la forma simpléctica .

Estas condiciones, que son fáciles de generalizar, surgen de la independencia del orden de diferenciación en el cálculo de las segundas derivadas. Entonces, para que un dQ diferencial , que es una función de cuatro variables para ser un diferencial exacto, hay seis condiciones que satisfacer.

En resumen, cuando un dQ diferencial es exacto:

• la función Q existe;
• $${\ displaystyle \ int _ {i} ^ {f} dQ = Q (f) -Q (i),} Independiente del camino seguido.

En termodinámica , cuando dQ es exacta, la función Q es una función de estado del sistema. Las funciones termodinámicas U , S , H , A y G son funciones de estado . En general, ni el trabajo ni el calor son funciones estatales. A veces, un diferencial exacto también se denomina "diferencial total" o "diferencial completo" o, en el estudio de la geometría diferencial , se denomina forma exacta .

Relaciones diferenciales parciales [ editar ]

Si tres variables, $${\ displaystyle x}, $${\ displaystyle y} y $${\ displaystyle z} están obligados por la condición $${\ displaystyle F (x, y, z) = {\ text {constant}}} para alguna función diferenciable $${\ displaystyle F (x, y, z)}, entonces existen los siguientes diferenciales totales ^{[1] : 667 y 669}

$${\ displaystyle dx = {\ left ({\ frac {\ partial x} {\ partial y}} \ right)} _ {z} \, dy + {\ left ({\ frac {\ partial x} {\ partial z }} \ right)} _ {y} \, dz}

$${\ displaystyle dz = {\ left ({\ frac {\ partial z} {\ partial x}} \ right)} _ {y} \, dx + {\ left ({\ frac {\ partial z} {\ partial y }} \ right)} _ {x} \, dy.}

Sustituyendo la primera ecuación en la segunda y reorganizando, obtenemos ^[1] : 669

$${\ displaystyle dz = {\ left ({\ frac {\ partial z} {\ partial x}} \ right)} _ {y} \ left [{\ left ({\ frac {\ partial x} {\ partial y }} \ derecha)} _ {z} dy + {\ izquierda ({\ frac {\ parcial x} {\ parcial z}} \ derecha)} _ {y} dz \ derecha] + {\ izquierda ({\ frac { \ partial z} {\ partial y}} \ right)} _ {x} dy,}

$${\ displaystyle dz = \ left [{\ left ({\ frac {\ partial z} {\ partial x}} \ right)} _ {y} {\ left ({\ frac {\ partial x} {\ partial y }} \ derecha)} _ {z} + {\ izquierda ({\ frac {\ parcial z} {\ parcial y}} \ derecha)} _ {x} \ derecha] dy + {\ izquierda ({\ frac {\ parcial z} {\ parcial x}} \ derecha)} _ {y} {\ izquierda ({\ frac {\ parcial x} {\ parcial z}} \ derecha)} _ {y} dz,}

$${\ displaystyle \ left [1 - {\ left ({\ frac {\ partial z} {\ partial x}} \ right)} _ {y} {\ left ({\ frac {\ partial x} {\ partial z }} \ derecha)} _ {y} \ derecha] dz = \ izquierda [{\ izquierda ({\ frac {\ parcial z} {\ parcial x}} \ derecha)} _ {y} {\ izquierda ({\ frac {\ parcial x} {\ parcial y}} \ derecha)} _ {z} + {\ izquierda ({\ frac {\ parcial z} {\ parcial y}} \ derecha)} _ {x} \ derecha] dy.}

Ya que $${\ displaystyle y} y $${\ displaystyle z} son variables independientes, $${\ displaystyle dy} y $${\ displaystyle dz}Puede ser elegido sin restricción. Para que esta última ecuación se mantenga en general, los términos entre corchetes deben ser iguales a cero. ^[1] : 669

Relación de reciprocidad [ editar ]

Establecer el primer término entre paréntesis igual a cero rendimientos ^[1]

$${\ displaystyle {\ left ({\ frac {\ partial z} {\ partial x}} \ right)} _ {y} {\ left ({\ frac {\ partial x} {\ partial z}} \ right) } _ {y} = 1.}

Un ligero reordenamiento da una relación de reciprocidad, ^[1] : 670

$${\ displaystyle {\ left ({\ frac {\ partial z} {\ partial x}} \ right)} _ {y} = {\ frac {1} {{\ left ({\ frac {\ partial x} { \ partial z}} \ right)} _ {y}}}.}

Hay dos permutaciones más de la derivación anterior que dan un total de tres relaciones de reciprocidad entre$${\ displaystyle x}, $${\ displaystyle y} y $${\ displaystyle z}. Las relaciones de reciprocidad muestran que lo inverso de una derivada parcial es igual a su recíproco.

Relación cíclica [ editar ]

La relación cíclica también se conoce como la regla cíclica o la regla del producto triple . Establecer el segundo término entre paréntesis igual a cero rendimientos ^[1] : 670

$${\ displaystyle {\ left ({\ frac {\ partial z} {\ partial x}} \ right)} _ {y} {\ left ({\ frac {\ partial x} {\ partial y}} \ right) } _ {z} = - {\ left ({\ frac {\ partial z} {\ partial y}} \ right)} _ {x}.}

Usando una relación de reciprocidad para $${\ displaystyle {\ tfrac {\ partial z} {\ partial y}}}en esta ecuación y el reordenamiento da una relación cíclica (la regla del producto triple ), ^[1] : 670

$${\ displaystyle {\ left ({\ frac {\ partial x} {\ partial y}} \ right)} _ {z} {\ left ({\ frac {\ partial y} {\ partial z}} \ right) } _ {x} {\ left ({\ frac {\ partial z} {\ partial x}} \ right)} _ {y} = - 1.}

Si, en cambio , una relación de reciprocidad para$${\ displaystyle {\ tfrac {\ partial x} {\ partial y}}}se utiliza con posterior reorganización, se obtiene una forma estándar para la diferenciación implícita :

$${\ displaystyle {\ left ({\ frac {\ partial y} {\ partial x}} \ right)} _ {z} = - {\ frac {{\ left ({\ frac {\ partial z} {\ partial x}} \ derecha)} _ {y}} {{\ izquierda ({\ frac {\ parcial z} {\ parcial y}} \ derecha)} _ {x}}}.}

Algunas ecuaciones útiles derivadas de diferenciales exactos en dos dimensiones [ editar ]

(Ver también ecuaciones termodinámicas de Bridgman para el uso de diferenciales exactos en la teoría de ecuaciones termodinámicas )

Supongamos que tenemos cinco funciones estatales $${\ displaystyle z, x, y, u}y $${\ displaystyle v}. Supongamos que el espacio de estado es bidimensional y cualquiera de las cinco cantidades son diferenciales exactos. Luego por la regla de la cadena

$${\ displaystyle (1) ~~~~~ dz = \ left ({\ frac {\ partial z} {\ partial x}} \ right) _ {y} dx + \ left ({\ frac {\ partial z} { \ parcial y}} \ derecha) _ {x} dy = \ izquierda ({\ frac {\ parcial z} {\ parcial u}} \ derecha) _ {v} du + \ izquierda ({\ frac {\ parcial z} {\ partial v}} \ right) _ {u} dv}

pero también por la regla de la cadena:

$${\ displaystyle (2) ~~~~~ dx = \ left ({\ frac {\ partial x} {\ partial u}} \ right) _ {v} du + \ left ({\ frac {\ partial x} { \ partial v}} \ right) _ {u} dv}

y

$${\ displaystyle (3) ~~~~~ dy = \ left ({\ frac {\ partial y} {\ partial u}} \ right) _ {v} du + \ left ({\ frac {\ partial y} { \ partial v}} \ right) _ {u} dv}

así que eso:

$${\ displaystyle (4) ~~~~~ dz = \ left [\ left ({\ frac {\ partial z} {\ partial x}} \ right) _ {y} \ left ({\ frac {\ partial x } {\ parcial u}} \ derecha) _ {v} + \ izquierda ({\ frac {\ parcial z} {\ parcial y}} \ derecha) _ {x} \ izquierda ({\ frac {\ parcial y} {\ parcial u}} \ derecha) _ {v} \ derecha] du}

$${\ displaystyle + \ left [\ left ({\ frac {\ partial z} {\ partial x}} \ right) _ {y} \ left ({\ frac {\ partial x} {\ partial v}} \ right ) _ {u} + \ left ({\ frac {\ partial z} {\ partial y}} \ right) _ {x} \ left ({\ frac {\ partial y} {\ partial v}} \ right) _ {u} \ right] dv}

lo que implica que:

$${\ displaystyle (5) ~~~~~ \ left ({\ frac {\ partial z} {\ partial u}} \ right) _ {v} = \ left ({\ frac {\ partial z} {\ partial x}} \ derecha) _ {y} \ izquierda ({\ frac {\ parcial x} {\ parcial u}} \ derecha) _ {v} + \ izquierda ({\ frac {\ parcial z} {\ parcial y }} \ derecha) _ {x} \ izquierda ({\ frac {\ parcial y} {\ parcial u}} \ derecha) _ {v}}

Dejando $${\ displaystyle v = y} da:

$${\ displaystyle (6) ~~~~~ \ left ({\ frac {\ partial z} {\ partial u}} \ right) _ {y} = \ left ({\ frac {\ partial z} {\ partial x}} \ derecha) _ {y} \ izquierda ({\ frac {\ parcial x} {\ parcial u}} \ derecha) _ {y}}

Dejando $${\ displaystyle u = y} da:

$${\ displaystyle (7) ~~~~~ \ left ({\ frac {\ partial z} {\ partial y}} \ right) _ {v} = \ left ({\ frac {\ partial z} {\ partial y}} \ derecha) _ {x} + \ izquierda ({\ frac {\ parcial z} {\ parcial x}} \ derecha) _ {y} \ izquierda ({\ frac {\ parcial x} {\ parcial y }} \ right) _ {v}}

Dejando $${\ displaystyle u = y}, $${\ displaystyle v = z} da:

$${\ displaystyle (8) ~~~~~ \ left ({\ frac {\ partial z} {\ partial y}} \ right) _ {x} = - \ left ({\ frac {\ partial z} {\ parcial x}} \ derecha) _ {y} \ izquierda ({\ frac {\ parcial x} {\ parcial y}} \ derecha) _ {z}}

utilizando ($${\ displaystyle \ parcial a / \ parcial b) _ {c} = 1 / (\ parcial b / \ parcial a) _ {c}}da la regla del producto triple :

$${\ displaystyle (9) ~~~~~ \ left ({\ frac {\ partial z} {\ partial x}} \ right) _ {y} \ left ({\ frac {\ partial x} {\ partial y }} \ derecha) _ {z} \ izquierda ({\ frac {\ parcial y} {\ parcial z}} \ derecha) _ {x} = - 1}

El exceso de potencial químico se define como la diferencia entre el potencial químico de una especie dada y el de un gas ideal en las mismas condiciones (en particular, a la misma presión , temperatura y composición ). ^[1]El potencial químico de una especie de partícula.$${\ displaystyle i} Por lo tanto, está dada por una parte ideal y una parte en exceso.

$${\ displaystyle \ mu _ {i} = \ mu _ {i} ^ {\ text {ideal}} + \ mu _ {i} ^ {\ text {exceso}}}

El potencial químico de un fluido puro puede estimarse mediante el método de inserción de Widom .

Medición y derivación [ editar ]

Para un sistema de diámetro. $${\ displaystyle L} y volumen $${\ displaystyle V}, a temperatura constante:$${\ displaystyle T}, la clásica función de particióncanónica $${\ displaystyle Q (N, V, T) = {\ frac {V ^ {N}} {\ Lambda ^ {dN} N!}} \ int _ {0} ^ {1} \ ldots \ int _ {0 } ^ {1} ds ^ {N} \ exp [- \ beta U (s ^ {N}; L)]} con $${\ displaystyle s} una coordenada escalada.

Por lo tanto, la energía libre está dada por

$${\ displaystyle F (N, V, T) = - k_ {B} T \ ln Q = -k_ {B} T \ ln \ left ({\ frac {V ^ {N}} {\ Lambda ^ {dN} N!}} \ Derecha) -k_ {B} T \ ln {\ int ds ^ {N} \ exp [- \ beta U (s ^ {N}; L)]} =}

$${\ displaystyle = F_ {id} (N, V, T) + F_ {ex} (N, V, T)}

combinando la ecuación anterior con la definición de potencial químico, $${\ displaystyle \ mu _ {a} = \ left ({\ frac {\ partial F} {\ partial N_ {a}}} \ right) _ {VT} = \ left ({\ frac {\ partial G} { \ parcial N_ {a}}} \ derecha) _ {PT}},

obtenemos el potencial químico de un sistema suficientemente grande (y el hecho de que el menor cambio permitido en el número de partículas es $${\ displaystyle \ Delta N = 1})

$${\ displaystyle \ mu = {\ frac {-k_ {B} T \ ln (Q_ {N + 1} / Q_ {N})} {\ Delta N}} {\ overset {\ Delta N = 1} {= }} - k_ {B} T \ ln \ left ({\ frac {V / \ Lambda ^ {d}} {N + 1}} \ right) -k_ {B} T \ ln {\ frac {\ int ds ^ {N + 1} \ exp [- \ beta U (s ^ {N + 1})]} {\ int ds ^ {N} \ exp [- \ beta U (s ^ {N})]}} = \ mu _ {id} (\ rho) + \ mu _ {ex}}

en donde el potencial químico de un gas ideal puede ser evaluado analíticamente. Ahora concentrémonos en$${\ displaystyle \ mu _ {ex}}, ya que la energía potencial de un sistema de partículas N + 1 se puede separar en la energía potencial de un sistema de partículas N y el potencial del exceso de partículas que interactúa con el sistema de partículas N, es decir,

$${\ displaystyle \ Delta U \ equiv U (s ^ {N + 1}) - U (s ^ {N})}

y

$${\ displaystyle \ mu _ {ex} = - k_ {B} T \ ln \ int ds_ {N + 1} \ langle \ exp (- \ beta \ Delta U) \ rangle _ {N}}.

Hasta el momento, convertimos el exceso de potencial químico en un promedio conjunto, y la integral en la ecuación anterior se puede muestrear mediante el método de fuerza bruta de Monte Carlo .

El cálculo del exceso de potencial químico no se limita a sistemas homogéneos, sino que también se ha extendido a sistemas no homogéneos por el método de inserción de Widom , u otros conjuntos como NPT y NVE.