TERMODINÁMICA

La temperatura de forjado es la temperatura a la cual un metal se vuelve sustancialmente más blando, pero es más bajo que la temperatura de fusión. ^[1] Llevar un metal a su temperatura de forjado permite cambiar la forma del metal aplicando una fuerza relativamente pequeña, sin crear grietas. La temperatura de forjado de una aleación estará entre las temperaturas de sus componentes metálicos. Para la mayoría de los metales, la temperatura de forjado será aproximadamente el 70% de la temperatura de fusión en kelvins .

La selección de la temperatura máxima de forjado permite que los metales se forjen más fácilmente, disminuyendo la presión de forjado y, por lo tanto, el desgaste de las matrices de formación de metal. ^[2] La temperatura a la que se forja un metal puede afectar la homogeneidad en la microestructura y las propiedades mecánicas de los productos forjados, lo que puede afectar mucho el rendimiento de los productos utilizados en la fabricación. ^[3]

Material	Temperatura de forja
	Celsius	Fahrenheit
Acero al carbono - 0,50% de contenido de carbono	1230 [2]	2246
Acero Inoxidable (No Magnético)	1150	2102
Acero inoxidable (magnético)	1095	2003
Níquel	1095	2003
Titanio	955	1751
Cobre	900	1652
Latón (25 tipos de aleación que utilizan diferentes proporciones: cobre y zinc)	815	1499
Bronce comercial (90% cobre y 10% estaño)	900 a 419.53	1652 a 787.154
Aluminio	300 - 480 [4]	600 - 900
Zinc	419.53	787.154
Dirigir	327.46	621.428
Estaño	231.93	449.474

De Wikipedia, la enciclopedia libre

  (Redirigido desde la expansión libre )

Saltar a navegaciónSaltar a búsqueda

La expansión Joule, en la que un volumen V _i = V ₀ se expande a un volumen V _f = 2 V ₀ en una cámara aislada térmicamente.

Se puede lograr una expansión libre de un gas moviendo el pistón más rápido que los átomos más rápidos del gas.

Esta expansión libre es casi estática (pero aún así irreversible).

La expansión Joule (también llamada expansión libre ) es un proceso irreversible en la termodinámica en el que se mantiene un volumen de gas en un lado de un contenedor aislado térmicamente (a través de una pequeña partición), y el otro lado del contenedor está siendo evacuado. La partición entre las dos partes del contenedor se abre y el gas llena todo el contenedor.

La expansión Joule, tratada como un experimento mental que involucra gases ideales , es un ejercicio útil en la termodinámica clásica. Proporciona un ejemplo conveniente para calcular cambios en cantidades termodinámicas, incluido el aumento resultante en la entropía del universo ( producción de entropía ) que resulta de este proceso intrínsecamente irreversible. Un experimento real de expansión de Joule implica necesariamente gases reales ; el cambio de temperatura en tal proceso proporciona una medida de fuerzas intermoleculares .

Este tipo de expansión lleva el nombre de James Prescott Joule,quien usó esta expansión, en 1845, en su estudio del equivalente mecánico del calor, pero esta expansión era conocida mucho antes que Joule, por ejemplo, por John Leslie , a principios del siglo XIX, y estudiado por Joseph-Louis Gay-Lussac en 1807 con resultados similares a los obtenidos por Joule. ^[1] [2]

La expansión Joule no debe confundirse con el efecto Joule-Thompson .

Descripción [ editar ]

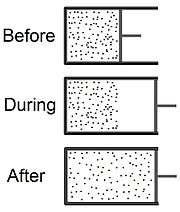
El proceso comienza con gas bajo cierta presión, $${\ displaystyle P _ {\ mathrm {i}}}a temperatura $${\ displaystyle T _ {\ mathrm {i}}}, confinado a la mitad de un contenedor aislado térmicamente (vea la parte superior del dibujo al principio de este artículo). El gas ocupa un volumen inicial.$${\ displaystyle V _ {\ mathrm {i}}}, separado mecánicamente de la otra parte del contenedor, que tiene un volumen $${\ displaystyle V _ {\ mathrm {0}}}, y esta bajo presion casi nula. El grifo (línea continua) entre las dos mitades del contenedor se abre repentinamente, y el gas se expande para llenar todo el contenedor, que tiene un volumen total de$${\ displaystyle V _ {\ mathrm {f}} = V _ {\ mathrm {i}} + V _ {\ mathrm {0}}}(ver parte inferior del dibujo). Un termómetro insertado en el compartimiento de la izquierda (no se muestra en el dibujo) mide la temperatura del gas antes y después de la expansión.

El sistema en este experimento consiste en ambos compartimentos; es decir, toda la región ocupada por el gas al final del experimento. Debido a que este sistema está aislado térmicamente, no puede intercambiar calor con su entorno. Además, dado que el volumen total del sistema se mantiene constante, el sistema no puede realizar trabajos en su entorno. ^[3] Como resultado, el cambio en la energía interna , $${\ displaystyle \ Delta U}, es cero. La energía interna consiste en energía cinética interna (debido al movimiento de las moléculas) y energía potencial interna (debido a fuerzas intermoleculares ). Cuando el movimiento molecular es aleatorio, la temperatura es la medida de la energía cinética interna. En este caso, la energía cinética interna se llama calor. Si las cámaras no han alcanzado el equilibrio, habrá un poco de energía cinética de flujo, que no es detectable por un termómetro (y, por lo tanto, no es un componente del calor). Por lo tanto, un cambio en la temperatura indica un cambio en la energía cinética, y parte de este cambio no aparecerá como calor hasta que, a menos que se restablezca el equilibrio térmico. Cuando el calor se transfiere a la energía cinética del flujo, esto causa una disminución de la temperatura ^[4]. En la práctica, el simple experimento de expansión libre de dos cámaras a menudo incorpora un "tapón poroso" a través del cual el aire en expansión debe fluir para alcanzar la cámara de presión más baja. El propósito de este tapón es inhibir el flujo direccional, acelerando así el restablecimiento del equilibrio térmico. Como la energía interna total no cambia, el estancamiento del flujo en la cámara receptora convierte la energía cinética del flujo nuevamente en movimiento aleatorio (calor), de modo que la temperatura sube a su valor predicho. Si la temperatura inicial del aire es lo suficientemente baja como para que las propiedades del gas no ideal causen condensación, parte de la energía interna se convierte en calor latente (un cambio de compensación en la energía potencial) en los productos líquidos. Por lo tanto, a bajas temperaturas, el proceso de expansión Joule proporciona información sobre las fuerzas intermoleculares.

Gases ideales [ editar ]

Si el gas es ideal, tanto la inicial ($${\ displaystyle T _ {\ mathrm {i}}}, $${\ displaystyle P _ {\ mathrm {i}}}, $${\ displaystyle V _ {\ mathrm {i}}}) y final ($${\ displaystyle T _ {\ mathrm {f}}}, $${\ displaystyle P _ {\ mathrm {f}}}, $${\ displaystyle V _ {\ mathrm {f}}}) Las condiciones siguen la Ley del Gas Ideal , por lo que inicialmente

$${\ displaystyle P _ {\ mathrm {i}} V _ {\ mathrm {i}} = nRT _ {\ mathrm {i}}}

y luego, después de abrir el grifo,

$${\ displaystyle P _ {\ mathrm {f}} V _ {\ mathrm {f}} = nRT _ {\ mathrm {f}}}.

aquí $${\ displaystyle n} es el numero de moles de gas y $${\ displaystyle R}Es la constante molar de gas ideal . Debido a que la energía interna no cambia y la energía interna de un gas ideal es únicamente una función de la temperatura, la temperatura del gas no cambia; por lo tanto$${\ displaystyle T _ {\ mathrm {i}} = T _ {\ mathrm {f}}}. Esto implica que

$${\ displaystyle P _ {\ mathrm {i}} V _ {\ mathrm {i}} = P _ {\ mathrm {f}} V _ {\ mathrm {f}} = nRT _ {\ mathrm {i}}}.

Por lo tanto, si el volumen se duplica, la presión se reduce a la mitad.

El hecho de que la temperatura no cambie hace que sea fácil calcular el cambio en la entropía del universo para este proceso.

Gases reales [ editar ]

A diferencia de los gases ideales, la temperatura de un gas real cambiará durante una expansión de Joule. Empíricamente, se encuentra que casi todos los gases se enfrían durante una expansión de Joule a todas las temperaturas investigadas; las excepciones son el helio, a temperaturas superiores a aproximadamente 40 K, y el hidrógeno, a temperaturas superiores a aproximadamente 200 K. Esta temperatura se conoce como la temperatura de inversión del gas. Por encima de esta temperatura, el gas se calienta durante la expansión de Joule. ^[5] [6] Dado que la energía interna es constante, el enfriamiento debe ser debido a la conversión de la energía cinética interna en energía potencial interna, y lo contrario es el caso del calentamiento.

Las fuerzas intermoleculares son repulsivas a corto plazo y atractivas a largo plazo (por ejemplo, vea el potencial de Lennard-Jones ). Dado que las distancias entre las moléculas de gas son grandes en comparación con los diámetros moleculares, la energía de un gas suele verse influida principalmente por la parte atractiva del potencial. Como resultado, la expansión de un gas generalmente aumenta la energía potencial asociada con las fuerzas intermoleculares. Algunos libros de texto dicen que para los gases este debe ser siempre el caso y que una expansión Joule siempre debe producir enfriamiento. ^[7] [8] En los líquidos, donde las moléculas están muy juntas, las interacciones repulsivas son mucho más importantes y es posible obtener un aumento de la temperatura durante una expansión de Joule. ^[9]

Teóricamente se predice que, a una temperatura suficientemente alta, todos los gases se calentarán durante una expansión de Joule ^[5]La razón es que en cualquier momento, un número muy pequeño de moléculas sufrirá colisiones; para esas pocas moléculas, las fuerzas de repulsión dominarán y la energía potencial será positiva. A medida que aumenta la temperatura, tanto la frecuencia de colisiones como la energía involucrada en las colisiones aumentan, por lo que la energía potencial positiva asociada con las colisiones aumenta considerablemente. Si la temperatura es lo suficientemente alta, eso puede hacer que la energía potencial total sea positiva, a pesar del número mucho mayor de moléculas que experimentan interacciones atractivas débiles. Cuando la energía potencial es positiva, una expansión de energía constante reduce la energía potencial y aumenta la energía cinética, lo que resulta en un aumento de la temperatura. Este comportamiento solo se ha observado para hidrógeno y helio; que tienen interacciones atractivas muy débiles.^[6]

Producción de entropía [ editar ]

La entropía es una función del estado y, por lo tanto, el cambio de entropía se puede calcular directamente a partir del conocimiento de los estados de equilibrio final e inicial. Para un gas ideal, el cambio en la entropía ^[10]es el mismo que para el efecto Joule-Thomson :

$${\ displaystyle \ Delta S = \ int _ {i} ^ {f} dS = \ int _ {V_ {i}} ^ {V_ {f}} {\ frac {P \, dV} {T}} = \ int _ {V_ {i}} ^ {V_ {f}} {\ frac {nR \, dV} {V}} = nR \ ln {\ frac {V_ {f}} {V_ {i}}}.}

Para un gas monoatómico ideal , la entropía en función de la energía interna U , el volumen V y el número de moles n viene dada por la ecuación de Sackur-Tetrode : ^[11]

$${\ displaystyle S = nR \ ln \ left [\ left ({\ frac {V} {N}} \ right) \ left ({\ frac {4 \ pi m} {3h ^ {2}}} {\ frac {U} {N}} \ derecha) ^ {\ frac {3} {2}} \ derecha] + {\ frac {5} {2}} nR.}

En esta expresión m es la masa de la partícula y h la constante de Planck. Para un gas ideal monoatómico U = (3/2) nRT = nC _V T , con C _V, la capacidad calorífica molar a volumen constante. En términos de la termodinámica clásica, la entropía de un gas ideal viene dada por

$${\ displaystyle S (V, T) = S_ {0} + nR \ ln \ left ({\ frac {V} {V_ {0}}} \ right) + nC_ {V} \ ln \ left ({\ frac {T} {T_ {0}}} \ derecha)}

donde S ₀ es el valor arbitrario elegido de la entropía en el volumen V ₀ y la temperatura T ₀ . ^[12] Se ve que una duplicación del volumen a la constante U o T conduce a un aumento de entropía de Δ S = nR ln (2). Este resultado también es válido si el gas no es monatómico, ya que la dependencia del volumen de la entropía es la misma para todos los gases ideales.

Una segunda forma de evaluar el cambio de entropía es elegir una ruta desde el estado inicial hasta el estado final donde todos los estados intermedios están en equilibrio. Dicha ruta solo puede realizarse en el límite donde los cambios ocurren infinitamente lentamente. Dichas rutas también se denominan rutas cuasiestáticas. En algunos libros se exige que una ruta cuasiestática sea reversible, aquí no agregamos esta condición adicional. El cambio neto de entropía del estado inicial al estado final es independiente de la elección particular de la ruta cuasiestática, ya que la entropía es una función del estado.

Así es como podemos efectuar la ruta cuasiestática. En lugar de dejar que el gas se someten a una expansión libre en el que se duplica el volumen, se permite una expansión libre en el que el volumen se expande por una cantidad muy pequeña δ V . Una vez que se alcanza el equilibrio térmico, dejamos que el gas experimente otra expansión libre de δ V y esperemos hasta que se alcance el equilibrio térmico. Repetimos esto hasta que el volumen se haya duplicado. En el límite de δ V a cero, esto se convierte en un proceso cuasiestático ideal, aunque irreversible. Ahora, según la relación termodinámica fundamental , tenemos:

$${\ displaystyle \ mathrm {d} U = T \ mathrm {d} SP \ mathrm {d} V.}

Como esta ecuación relaciona los cambios en las variables de estado termodinámico, es válida para cualquier cambio cuasiestático, independientemente de si es irreversible o reversible. Para la ruta definida anteriormente tenemos que d U = 0 y, por lo tanto, T d S = P d V , y por lo tanto el aumento en la entropía para la expansión Joule es

$${\ displaystyle \ Delta S = \ int _ {i} ^ {f} \ mathrm {d} S = \ int _ {V_ {0}} ^ {2V_ {0}} {\ frac {P \, \ mathrm { d} V} {T}} = \ int _ {V_ {0}} ^ {2V_ {0}} {\ frac {nR \, \ mathrm {d} V} {V}} = nR \ ln 2.}

Una tercera forma de calcular el cambio de entropía consiste en una ruta que consiste en una expansión adiabática reversible seguida de calentamiento. Primero dejamos que el sistema experimente una expansión adiabática reversible en la que el volumen se duplica. Durante la expansión, el sistema realiza el trabajo y la temperatura del gas baja, por lo que tenemos que suministrar calor al sistema igual al trabajo realizado para llevarlo al mismo estado final que en el caso de la expansión de Joule.

Durante la expansión adiabática reversible, tenemos d S = 0. De la expresión clásica para la entropía se puede deducir que la temperatura después de la duplicación del volumen en entropía constante se da como:

$${\ displaystyle T = T_ {i} 2 ^ {- R / C_ {V}} = T_ {i} 2 ^ {- 2/3}}

Para el gas ideal monoatómico. Calentar el gas hasta la temperatura inicial T _i aumenta la entropía en la cantidad

$${\ displaystyle \ Delta S = n \ int _ {T} ^ {T_ {i}} C_ {V} {\ frac {\ mathrm {d} T '} {T'}} = nR \ ln 2.}

Podríamos preguntarnos cuál sería el trabajo si, una vez que se haya producido la expansión Joule, el gas se devuelva al lado izquierdo comprimiéndolo. El mejor método (es decir, el método que implica el menor trabajo) es el de una compresión isotérmica reversible, que tomaría el trabajo W dado por

$${\ displaystyle W = - \ int _ {2V_ {0}} ^ {V_ {0}} P \, \ mathrm {d} V = - \ int _ {2V_ {0}} ^ {V_ {0}} { \ frac {nRT} {V}} \ mathrm {d} V = nRT \ ln 2 = T \ Delta S_ {gas}.}

Durante la expansión de Joule, el entorno no cambia, por lo que la entropía del entorno es constante. Entonces, el cambio de entropía del llamado "universo" es igual al cambio de entropía del gas que es nR  ln 2.

Efecto de gas real [ editar ]

Joule realizó su experimento con aire a temperatura ambiente, que se expandió de una presión de aproximadamente 22 bar. El aire, en estas condiciones, es casi un gas ideal, pero no del todo. Como resultado, el cambio de temperatura real no será exactamente cero. Con nuestro conocimiento actual de las propiedades termodinámicas del aire ^[13] , podemos calcular que la temperatura del aire debería bajar unos 3 grados Celsius cuando el volumen se duplica en condiciones adiabáticas. Sin embargo, debido a la baja capacidad de calor del aire y la alta capacidad de calor de los fuertes contenedores de cobre y el agua del calorímetro, la caída de temperatura observada es mucho menor, por lo que Joule encontró que el cambio de temperatura era cero dentro de su precisión de medición.