LISTAS DE FORMAS - TRIÁNGULOS

biológica, ver Circunscripción (taxonomía) .

Círculo circunscrito, C , y circuncentro, O , de un polígono cíclico , P

En geometría , el círculo circunscrito o circunferencial de un polígono es un círculo que atraviesa todos los vértices del polígono. El centro de este círculo se llama circuncentro y su radio se llama circunradio .

Un polígono que tiene un círculo circunscrito se llama polígono cíclico (a veces un polígono cíclico , porque los vértices son cíclicos ). Todos los polígonos simples regulares , todos los trapecios isósceles , todos los triángulos y todos los rectángulos son cíclicos.

Una noción relacionada es la de un círculo de límite mínimo , que es el círculo más pequeño que contiene completamente el polígono dentro de él, si su centro no está fuera del polígono. No todos los polígonos tienen un círculo circunscrito, ya que los vértices de un polígono no necesitan estar todos en un círculo, pero cada polígono tiene un círculo de límite mínimo único, que puede construirse mediante un algoritmo de tiempo lineal . ^[2] Incluso si un polígono tiene un círculo circunscrito, puede no coincidir con su círculo límite mínimo; por ejemplo, para un triángulo obtuso , el círculo límite mínimo tiene el lado más largo como diámetro y no pasa a través del vértice opuesto.

Triángulos [ editar ]

Todos los triángulos son cíclicos; es decir, cada triángulo tiene un círculo circunscrito.

Construcción de regla y brújula [ editar ]

Construcción del círculo circunferencial (rojo) y el circuncentro Q (punto rojo)

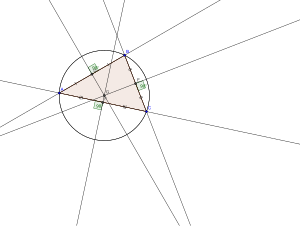
El circuncentro de un triángulo puede construirse dibujando dos de las tres bisectrices perpendiculares . Para tres puntos no colineales, estas dos líneas no pueden ser paralelas, y el circuncentro es el punto donde se cruzan. Cualquier punto en la bisectriz es equidistante de los dos puntos que bisecta, de lo que se deduce que este punto, en ambas bisectrices, es equidistante de los tres vértices triangulares. El circunradio es la distancia desde él a cualquiera de los tres vértices.

Construcción alternativa [ editar ]

Construcción alternativa del circuncentro (intersección de líneas discontinuas)

Un método alternativo para determinar el circuncentro es dibujar cualquiera de las dos líneas que salen cada una de uno de los vértices en un ángulo con el lado común, siendo el ángulo de salida común 90 ° menos el ángulo del vértice opuesto. (En el caso de que el ángulo opuesto sea obtuso, dibujar una línea en un ángulo negativo significa salir del triángulo).

En la navegación costera , el círculo circunferencial de un triángulo a veces se usa como una forma de obtener una línea de posición usando un sextante cuando no hay una brújula disponible. El ángulo horizontal entre dos puntos de referencia define el círculo en el que se encuentra el observador.

Ecuaciones de circunferencia [ editar ]

Coordenadas cartesianas [ editar ]

En el plano euclídeo , es posible dar explícitamente una ecuación del círculo circunferencial en términos de las coordenadas cartesianas de los vértices del triángulo inscrito. Suponer que

{\ displaystyle {\ begin {alineado} \ mathbf {A} & = (A_ {x}, A_ {y}) \\\ mathbf {B} & = (B_ {x}, B_ {y}) \\\ mathbf {C} & = (C_ {x}, C_ {y}) \ end {alineado}}}

son las coordenadas de los puntos A , B , y C . El círculo circunferencial es entonces el lugar geométrico de los puntos v = ( v _x , v _y ) en el plano cartesiano que satisface las ecuaciones.

{\ displaystyle {\ begin {alineado} | \ mathbf {v} - \ mathbf {u} | ^ {2} & = r ^ {2} \\ | \ mathbf {A} - \ mathbf {u} | ^ { 2} & = r ^ {2} \\ | \ mathbf {B} - \ mathbf {u} | ^ {2} & = r ^ {2} \\ | \ mathbf {C} - \ mathbf {u} | ^ {2} & = r ^ {2} \ end {alineado}}}

garantizando que los puntos A , B , C y v están todos a la misma distancia r del centro común u del círculo. Usando la identidad de polarización , estas ecuaciones se reducen a la condición de que la matriz

{\ displaystyle {\ begin {bmatrix} | \ mathbf {v} | ^ {2} & - 2v_ {x} & - 2v_ {y} & - 1 \\ | \ mathbf {A} | ^ {2} & - 2A_ {x} & - 2A_ {y} & - 1 \\ | \ mathbf {B} | ^ {2} & - 2B_ {x} & - 2B_ {y} & - 1 \\ | \ mathbf {C} | ^ {2} & - 2C_ {x} & - 2C_ {y} & - 1 \ end {bmatrix}}}

tiene un núcleo distinto de cero . Por lo tanto, el círculo circunferencial puede describirse alternativamente como el lugar geométrico de los ceros del determinante de esta matriz:

{\ displaystyle \ det {\ begin {bmatrix} | \ mathbf {v} | ^ {2} y v_ {x} y v_ {y} y 1 \\ | \ mathbf {A} | ^ {2} y A_ {x} y A_ { y} y 1 \\ | \ mathbf {B} | ^ {2} y B_ {x} y B_ {y} y 1 \\ | \ mathbf {C} | ^ {2} y C_ {x} y C_ {y} y 1 \ end { bmatrix}} = 0.}

Usando la expansión del cofactor , deje

${\displaystyle {\begin{aligned}S_{x}&={\frac {1}{2}}\det {\begin{bmatrix}|\mathbf {A} |^{2}&A_{y}&1\\|\mathbf {B} |^{2}&B_{y}&1\\|\mathbf {C} |^{2}&C_{y}&1\end{bmatrix}},\\[5pt]S_{y}&={\frac {1}{2}}\det {\begin{bmatrix}A_{x}&|\mathbf {A} |^{2}&1\\B_{x}&|\mathbf {B} |^{2}&1\\C_{x}&|\mathbf {C} |^{2}&1\end{bmatrix}},\\[5pt]a&=\det {\begin{bmatrix}A_{x}&A_{y}&1\\B_{x}&B_{y}&1\\C_{x}&C_{y}&1\end{bmatrix}},\\[5pt]b&=\det {\begin{bmatrix}A_{x}&A_{y}&|\mathbf {A} |^{2}\\B_{x}&B_{y}&|\mathbf {B} |^{2}\\C_{x}&C_{y}&|\mathbf {C} |^{2}\end{bmatrix}}\end{aligned}}}$

entonces tenemos un | v | ² - 2 Sv - b = 0 y, suponiendo que los tres puntos no estuvieran en una línea (de lo contrario, el círculo es esa línea que también puede verse como un círculo generalizado con S en el infinito), | v - S / a | ² = b / a + | S | ² / a ² , dando el circuncentro S / a y el circunradio √ b / a + | S | ² / a ². Un enfoque similar permite deducir la ecuación de la circunferencia de un tetraedro .

Ecuación paramétrica [ editar ]

Un vector unitario perpendicular al plano que contiene el círculo viene dado por

$${\ displaystyle {\ widehat {n}} = {\ frac {(P_ {2} -P_ {1}) \ times (P_ {3} -P_ {1})} {| (P_ {2} -P_ { 1}) \ times (P_ {3} -P_ {1}) |}}.}

Por lo tanto, dado el radio, r , centro, P _c , un punto en el círculo, P ₀ y una unidad normal del plano que contiene el círculo,$${\ textstyle {\ widehat {n}}}, una ecuación paramétrica del círculo que comienza en el punto P ₀ y continúa en sentido positivo (es decir, diestro ) sobre$${\ displaystyle \ scriptstyle {\ widehat {n}}} es el siguiente:

$${\ displaystyle \ mathrm {R} (s) = \ mathrm {P_ {c}} + \ cos \ left ({\ frac {\ mathrm {s}} {\ mathrm {r}}} \ right) (P_ { 0} -P_ {c}) + \ sin \ left ({\ frac {\ mathrm {s}} {\ mathrm {r}}} \ right) \ left [{\ widehat {n}} \ times (P_ { 0} -P_ {c}) \ right].}

Coordenadas trilineales y baricéntricas [ editar ]

Una ecuación para el círculo circunferencial en coordenadas trilineales x  : y  : z es ^{[1] : p. 199} a / x + b / y + c / z = 0 . Una ecuación para el círculo circunferencial en coordenadas barcéntricas x  : y  : z es a ² / x + b ² / y + c ² / z = 0 .

El conjugado isogonal del círculo es la línea en el infinito, dada en coordenadas trilineales por ax + by + cz = 0 y en coordenadas barcéntricas por x + y + z = 0 .

Dimensiones superiores [ editar ]

Además, el círculo de un triángulo incrustado en d dimensiones se puede encontrar utilizando un método generalizado. Deje que A , B , y C sea d puntos -dimensional, que forman los vértices de un triángulo. Comenzamos transponiendo el sistema para colocar C en el origen:

{\ displaystyle {\ begin {alineado} \ mathbf {a} & = \ mathbf {A} - \ mathbf {C}, \\\ mathbf {b} & = \ mathbf {B} - \ mathbf {C}. \ end {alineado}}}

El circunradio, r , es entonces

$${\ displaystyle r = {\ frac {\ left \ | \ mathbf {a} \ right \ | \ left \ | \ mathbf {b} \ right \ | \ left \ | \ mathbf {a} - \ mathbf {b} \ right \ |} {2 \ left \ | \ mathbf {a} \ times \ mathbf {b} \ right \ |}} = {\ frac {\ left \ | \ mathbf {a} - \ mathbf {b} \ right \ |} {2 \ sin \ theta}} = {\ frac {\ left \ | \ mathbf {A} - \ mathbf {B} \ right \ |} {2 \ sin \ theta}},}

donde θ es el ángulo interior entre una y b . El circuncentro, p ₀ , viene dado por

$${\ displaystyle p_ {0} = {\ frac {(\ left \ | \ mathbf {a} \ right \ | ^ {2} \ mathbf {b} - \ left \ | \ mathbf {b} \ right \ | ^ {2} \ mathbf {a}) \ times (\ mathbf {a} \ times \ mathbf {b})} {2 \ left \ | \ mathbf {a} \ times \ mathbf {b} \ right \ | ^ { 2}}} + \ mathbf {C}.}

Esta fórmula solo funciona en tres dimensiones ya que el producto cruzado no está definido en otras dimensiones, pero se puede generalizar a las otras dimensiones reemplazando los productos cruzados con las siguientes identidades:

{\ displaystyle {\ begin {alineado} (\ mathbf {a} \ times \ mathbf {b}) \ times \ mathbf {c} & = (\ mathbf {a} \ cdot \ mathbf {c}) \ mathbf {b } - (\ mathbf {b} \ cdot \ mathbf {c}) \ mathbf {a}, \\\ mathbf {a} \ times (\ mathbf {b} \ times \ mathbf {c}) & = (\ mathbf {a} \ cdot \ mathbf {c}) \ mathbf {b} - (\ mathbf {a} \ cdot \ mathbf {b}) \ mathbf {c}, \\\ left \ | \ mathbf {a} \ times \ mathbf {b} \ right \ | & = {\ sqrt {\ left \ | \ mathbf {a} \ right \ | ^ {2} \ left \ | \ mathbf {b} \ right \ | ^ {2} - (\ mathbf {a} \ cdot \ mathbf {b}) ^ {2}}}. \ end {alineado}}}

Coordenadas del circuncentro [ editar ]

Coordenadas cartesianas [ editar ]

Las coordenadas cartesianas del circuncentro$${\ displaystyle U = \ left (U_ {x}, U_ {y} \ right)} son

{\ displaystyle {\ begin {alineado} U_ {x} & = {\ frac {1} {D}} \ left [(A_ {x} ^ {2} + A_ {y} ^ {2}) (B_ { y} -C_ {y}) + (B_ {x} ^ {2} + B_ {y} ^ {2}) (C_ {y} -A_ {y}) + (C_ {x} ^ {2} + C_ {y} ^ {2}) (A_ {y} -B_ {y}) \ right] \\ [5pt] U_ {y} & = {\ frac {1} {D}} \ left [(A_ { x} ^ {2} + A_ {y} ^ {2}) (C_ {x} -B_ {x}) + (B_ {x} ^ {2} + B_ {y} ^ {2}) (A_ { x} -C_ {x}) + (C_ {x} ^ {2} + C_ {y} ^ {2}) (B_ {x} -A_ {x}) \ right] \ end {alineado}}}

con

$${\ displaystyle D = 2 \ left [A_ {x} (B_ {y} -C_ {y}) + B_ {x} (C_ {y} -A_ {y}) + C_ {x} (A_ {y} -Por derecho].\,}

Sin pérdida de generalidad, esto se puede expresar de forma simplificada después de la traducción del vértice A al origen de los sistemas de coordenadas cartesianas, es decir, cuando A ′ = A - A = ( A ′ _x , A ′ _y ) = (0, 0) . En este caso, las coordenadas de los vértices B '= B - A y C ' = C - A representan los vectores desde el vértice A 'hasta estos vértices. Observe que esta traducción trivial es posible para todos los triángulos y el circuncentro$${\ displaystyle U '= (U' _ {x}, U '_ {y})}del triángulo A ′ B ′ C ′ seguir como

{\ displaystyle {\ begin {alineado} U '_ {x} & = {\ frac {1} {D'}} \ left [C '_ {y} ({B' _ {x}} ^ {2} + {B '_ {y}} ^ {2}) - B' _ {y} ({C '_ {x}} ^ {2} + {C' _ {y}} ^ {2}) \ right ], \\ [5pt] U '_ {y} & = {\ frac {1} {D'}} \ left [B '_ {x} ({C' _ {x}} ^ {2} + { C '_ {y}} ^ {2}) - C' _ {x} ({B '_ {x}} ^ {2} + {B' _ {y}} ^ {2}) \ right] \ end {alineado}}}

con

$${\ displaystyle D '= 2 (B' _ {x} C '_ {y} -B' _ {y} C '_ {x}). \,}

Debido a la traducción del vértice A al origen, el circunradio r se puede calcular como

$${\ displaystyle r = \ | U '\ | = {\ sqrt {{U' _ {x}} ^ {2} + {U '_ {y}} ^ {2}}}}

y el circuncentro real de ABC sigue como

$${\ displaystyle U = U '+ A}

Coordenadas trilineales [ editar ]

El circuncentro tiene coordenadas trilineales ^[1] : p.19

cos α  : cos β  : cos γ

donde α , β , γ son los ángulos del triángulo.

En términos de las longitudes laterales a, b, c , los trilineales son ^[2]

$${\ displaystyle a \ left (b ^ {2} + c ^ {2} -a ^ {2} \ right): b \ left (c ^ {2} + a ^ {2} -b ^ {2} \ derecha): c \ left (a ^ {2} + b ^ {2} -c ^ {2} \ right).}

Coordenadas barcéntricas [ editar ]

El circuncentro tiene coordenadas barcéntricas.

$${\ displaystyle a ^ {2} \ left (b ^ {2} + c ^ {2} -a ^ {2} \ right): \; b ^ {2} \ left (c ^ {2} + a ^ {2} -b ^ {2} \ right): \; c ^ {2} \ left (a ^ {2} + b ^ {2} -c ^ {2} \ right), \,}^[3]

donde a , b , c son longitudes de borde ( BC , CA , AB respectivamente) del triángulo.

En términos de los ángulos del triángulo. $${\ displaystyle \ alpha, \ beta, \ gamma,}las coordenadas barcéntricas del circuncentro son ^[2]

$${\ displaystyle \ sin 2 \ alpha: \ sin 2 \ beta: \ sin 2 \ gamma.}

Vector de circuncentro [ editar ]

Dado que las coordenadas cartesianas de cualquier punto son un promedio ponderado de las de los vértices, siendo los pesos las coordenadas barcéntricas del punto normalizadas para sumar unidades, el vector circuncentro se puede escribir como

$${\ displaystyle U = {\ frac {a ^ {2} \ left (b ^ {2} + c ^ {2} -a ^ {2} \ right) A + b ^ {2} \ left (c ^ { 2} + a ^ {2} -b ^ {2} \ right) B + c ^ {2} \ left (a ^ {2} + b ^ {2} -c ^ {2} \ right) C} { a ^ {2} \ left (b ^ {2} + c ^ {2} -a ^ {2} \ right) + b ^ {2} \ left (c ^ {2} + a ^ {2} -b ^ {2} \ right) + c ^ {2} \ left (a ^ {2} + b ^ {2} -c ^ {2} \ right)}}.}

Aquí U es el vector del circuncentro y A, B, C son los vectores de vértice. El divisor aquí es igual a 16 S ² donde S es el área del triángulo.

Coordenadas cartesianas de productos cruzados y de punto [ editar ]

En el espacio euclidiano , hay un círculo único que pasa por cualquiera de los tres puntos no colineales P ₁ , P ₂ y P ₃ . Usando coordenadas cartesianas para representar estos puntos como vectores espaciales , es posible usar el producto punto y el producto cruzado para calcular el radio y el centro del círculo. Dejar

$${\ displaystyle \ mathrm {P_ {1}} = {\ begin {bmatrix} x_ {1} \\ y_ {1} \\ z_ {1} \ end {bmatrix}}, \ mathrm {P_ {2}} = {\ begin {bmatrix} x_ {2} \\ y_ {2} \\ z_ {2} \ end {bmatrix}}, \ mathrm {P_ {3}} = {\ begin {bmatrix} x_ {3} \\ y_ {3} \\ z_ {3} \ end {bmatrix}}}

Entonces el radio del círculo viene dado por

$${\ displaystyle \ mathrm {r} = {\ frac {\ left | P_ {1} -P_ {2} \ right | \ left | P_ {2} -P_ {3} \ right | \ left | P_ {3} -P_ {1} \ right |} {2 \ left | \ left (P_ {1} -P_ {2} \ right) \ times \ left (P_ {2} -P_ {3} \ right) \ right |} }}

El centro del círculo viene dado por la combinación lineal.

$${\ displaystyle \ mathrm {P_ {c}} = \ alpha \, P_ {1} + \ beta \, P_ {2} + \ gamma \, P_ {3}}

dónde

$${\ displaystyle {\ begin {alineado} \ alpha = {\ frac {\ left | P_ {2} -P_ {3} \ right | ^ {2} \ left (P_ {1} -P_ {2} \ right) \ cdot \ left (P_ {1} -P_ {3} \ right)} {2 \ left | \ left (P_ {1} -P_ {2} \ right) \ times \ left (P_ {2} -P_ { 3} \ right) \ right | ^ {2}}} \\\ beta = {\ frac {\ left | P_ {1} -P_ {3} \ right | ^ {2} \ left (P_ {2} - P_ {1} \ right) \ cdot \ left (P_ {2} -P_ {3} \ right)} {2 \ left | \ left (P_ {1} -P_ {2} \ right) \ times \ left ( P_ {2} -P_ {3} \ right) \ right | ^ {2}}} \\\ gamma = {\ frac {\ left | P_ {1} -P_ {2} \ right | ^ {2} \ left (P_ {3} -P_ {1} \ right) \ cdot \ left (P_ {3} -P_ {2} \ right)} {2 \ left | \ left (P_ {1} -P_ {2} \ right) \ times \ left (P_ {2} -P_ {3} \ right) \ right | ^ {2}}} \ end {alineado}}}

Ubicación relativa al triángulo [ editar ]

La posición del circuncentro depende del tipo de triángulo:

• Si y solo si un triángulo es agudo (todos los ángulos son más pequeños que un ángulo recto), el circuncentro se encuentra dentro del triángulo.
• Si y solo si es obtuso (tiene un ángulo más grande que un ángulo recto), el circuncentro se encuentra fuera del triángulo.
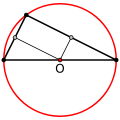
• Si y solo si es un triángulo rectángulo, el circuncentro se encuentra en el centro de la hipotenusa . Esta es una forma del teorema de Tales .

• 

  El circuncentro de un triángulo agudo está dentro del triángulo.
 
• 

  El circuncentro de un triángulo rectángulo está en el centro de la hipotenusa.
 
• 

  El circuncentro de un triángulo obtuso está fuera del triángulo.

Estas características de ubicación se pueden ver considerando las coordenadas trilineales o baricéntricas dadas anteriormente para el circuncentro: las tres coordenadas son positivas para cualquier punto interior, al menos una coordenada es negativa para cualquier punto exterior, y una coordenada es cero y dos son positivas para un punto sin vértice en un lado del triángulo.

Ángulos [ editar ]

Los ángulos que forma el círculo circunscrito con los lados del triángulo coinciden con los ángulos en los que los lados se encuentran. El ángulo opuesto lateral α se encuentra con el círculo dos veces: una vez en cada extremo; en cada caso en ángulo α (de manera similar para los otros dos ángulos). Esto se debe al teorema del segmento alternativo , que establece que el ángulo entre la tangente y el acorde es igual al ángulo en el segmento alternativo.

El triángulo se centra en el círculo del triángulo ABC [ editar ]

En esta sección, los ángulos de vértice están etiquetados como A , B , C y todas las coordenadas son coordenadas trilineales :

• Punto de Steiner = bc / ( b ² - c ² ): ca / ( c ² - a ² ): ab / ( a ² - b ² ) = el punto de intersección no vértice del círculo con la elipse de Steiner. (La elipse de Steiner , con centro = centroide ( ABC ), es la elipse de menor área que pasa por A , B y C. Una ecuación para esta elipse es 1 / ( ax ) + 1 / ( by ) + 1 / (cz ) = 0. )
• Punto de retención = seg ( A + ω): seg ( B + ω): seg ( C + ω) = antípoda del punto Steiner
• Foco de la parábola de Kiepert = csc ( B - C ): csc ( C - A ): csc ( A - B ).

Otras propiedades [ editar ]

El diámetro del circunferencia circunscrita , llamado circundiametro e igual al doble del circunradio , se puede calcular como la longitud de cualquier lado del triángulo dividido por el seno del ángulo opuesto :

$${\ displaystyle {\ text {diámetro}} = {\ frac {a} {\ sin A}} = {\ frac {b} {\ sin B}} = {\ frac {c} {\ sin C}}. }

Como consecuencia de la ley de los senos , no importa qué lado y ángulo opuesto se tomen: el resultado será el mismo.

El diámetro del círculo circunferencial también se puede expresar como

{\ displaystyle {\ begin {alineado} {\ text {diámetro}} & {} = {\ frac {abc} {2 \ cdot {\ text {area}}}} = {\ frac {| AB || BC | | CA |} {2 | \ Delta ABC |}} \\ [5pt] & {} = {\ frac {abc} {2 {\ sqrt {s (sa) (sb) (sc)}}}} \\ [5pt] & {} = {\ frac {2abc} {\ sqrt {(a + b + c) (- a + b + c) (a-b + c) (a + bc)}}} \ end { alineado}}}

donde a , b , c son las longitudes de los lados del triángulo y s = ( a + b + c ) / 2 es el semiperímetro. La expresion$${\ displaystyle {\ sqrt {\ scriptstyle {s (sa) (sb) (sc)}}}}arriba está el área del triángulo, según la fórmula de Heron . ^[3] Las expresiones trigonométricas para el diámetro del círculo circunferencial incluyen ^{[4] : p.379}

$${\ displaystyle {\ text {diámetro}} = {\ sqrt {\ frac {2 \ cdot {\ text {area}}} {\ sin A \ sin B \ sin C}}}.}

El círculo de nueve puntos del triángulo tiene la mitad del diámetro del círculo .

En cualquier triángulo dado, el circuncentro siempre es colineal con el centroide y el ortocentro . La línea que pasa por todos ellos se conoce como la línea de Euler .

El conjugado isogonal del circuncentro es el ortocentro .

El círculo límite mínimo útil de tres puntos está definido por el círculo circunferencial (donde tres puntos están en el círculo límite mínimo) o por los dos puntos del lado más largo del triángulo (donde los dos puntos definen un diámetro del círculo). Es común confundir el círculo límite mínimo con el círculo circunferencial.

El círculo de tres puntos colineales es la línea en la que se encuentran los tres puntos, a menudo referidos como un círculo de radio infinito . Los puntos casi colineales a menudo conducen a la inestabilidad numérica en el cálculo del círculo circunferencial.

Los círculos de triángulos tienen una relación íntima con la triangulación de Delaunay de un conjunto de puntos.

Según el teorema de Euler en geometría , la distancia entre el circuncentro O y el incentro I es

$${\ displaystyle OI = {\ sqrt {R (R-2r)}},}

donde r es el radio del círculo y R es el radio del círculo ; por lo tanto, el circunradio es al menos dos veces el inradius ( desigualdad del triángulo de Euler ), con igualdad solo en el caso equilátero . ^{[5] [6] : pág. 198}

La distancia entre O y el ortocentro H es ^{[7] [8] : p. 449}

$${\ displaystyle OH = {\ sqrt {R ^ {2} -8R ^ {2} \ cos A \ cos B \ cos C}} = {\ sqrt {9R ^ {2} - (a ^ {2} + b ^ {2} + c ^ {2})}}.}

Para el centroide G y el centro N de nueve puntos tenemos

{\ displaystyle {\ begin {alineado} IG &

El producto de la radio de circunferencia inscrita y el radio de circunferencia circunscrita de un triángulo con lados a , b , y c es ^{[9] : p. 189, n.º 298 (d)}

$${\ displaystyle rR = {\ frac {abc} {2 (a + b + c)}}.}

Con circunradio R , lados a , b , c y medianas m _a , m _b y m _c , tenemos ^{[10] : p.289–290}

{\ displaystyle {\ begin {alineado} 3 {\ sqrt {3}} R & \ geq a + b + c \\ [5pt] 9R ^ {2} & \ geq a ^ {2} + b ^ {2} + c ^ {2} \\ [5pt] {\ frac {27} {4}} R ^ {2} & \ geq m_ {a} ^ {2} + m_ {b} ^ {2} + m_ {c} ^ {2}. \ End {alineado}}}

Si la mediana m , la altitud h y la bisectriz interna t emanan del mismo vértice de un triángulo con circunradio R , entonces ^{[11] : p.122, # 96}

$${\ displaystyle 4R ^ {2} h ^ {2} (t ^ {2} -h ^ {2}) = t ^ {4} (m ^ {2} -h ^ {2}).}

El teorema de Carnot establece que la suma de las distancias desde el circuncentro a los tres lados es igual a la suma del circunradio y el inradio . ^{[11] : p.83} Aquí la longitud de un segmento se considera negativa si y solo si el segmento se encuentra completamente fuera del triángulo.

Si un triángulo tiene dos círculos particulares como su circunferencia circunferencial e incírculo , existe un número infinito de otros triángulos con la misma circunferencia circunferencial e incircle, con cualquier punto en la circunferencia circunscrita como un vértice. (Este es el caso n  = 3 del porismo de Poncelet ). Una condición necesaria y suficiente para que existan tales triángulos es la igualdad anterior$${\ displaystyle OI = {\ sqrt {R (R-2r)}}.}^{[9] : pág. 188}

Cuadriláteros cíclicos [ editar ]

Cuadriláteros cíclicos

Artículo principal: cuadrilátero cíclico

Los cuadriláteros que pueden circunscribirse tienen propiedades particulares, incluido el hecho de que los ángulos opuestos son ángulos suplementarios (que suman 180 ° o π radianes).

N -gones cíclicos [ editar ]

Para un polígono cíclico con un número impar de lados, todos los ángulos son iguales si y solo si el polígono es regular. Un polígono cíclico con un número par de lados tiene todos los ángulos iguales si y solo si los lados alternos son iguales (es decir, los lados 1, 3, 5, ... son iguales, y los lados 2, 4, 6, ... son iguales). ^[12]

Un pentágono cíclico con lados y área racionales se conoce como pentágono de Robbins ; En todos los casos conocidos, sus diagonales también tienen longitudes racionales. ^[13]

En cualquier n -gon cíclico con n par , la suma de un conjunto de ángulos alternos (el primero, tercero, quinto, etc.) es igual a la suma del otro conjunto de ángulos alternos. Esto puede probarse mediante la inducción del caso n = 4, en cada caso reemplazando un lado con tres lados más y observando que estos tres lados nuevos junto con el lado anterior forman un cuadrilátero que tiene esta propiedad; Los ángulos alternos del último cuadrilátero representan las adiciones a las sumas de ángulos alternos del n -gon anterior .

Deje que un n -gon se inscriba en un círculo, y que otro n -gon sea tangencial a ese círculo en los vértices del primer n -gon. Luego, desde cualquier punto P en el círculo, el producto de las distancias perpendiculares desde P a los lados del primer n -gon es igual al producto de las distancias perpendiculares desde P a los lados del segundo n -gon. ^{[9] : pág. 72}

Punto en la circunferencia circunscrita [ editar ]

Deje que un n -gon cíclico tenga vértices A ₁ , ..., A _n en el círculo unitario. Entonces, para cualquier punto M en el arco menor A ₁ A _n , las distancias desde M hasta los vértices satisfacen ^{[14] : p.190, # 332.10}

{\ displaystyle {\ begin {cases} MA_ {1} + MA_ {3} + \ cdots + MA_ {n-2} + MA_ {n}

Polígono que circunscribe constante [ editar ]

Una secuencia de polígonos y círculos circunscritos.

Cualquier polígono regular es cíclico. Considere un círculo unitario, luego circunscriba un triángulo regular de modo que cada lado toque el círculo. Circunde un círculo, luego circunscriba un cuadrado. Nuevamente circunscriba un círculo, luego circunscriba un 5-gon regular, y así sucesivamente. Los radios de los círculos circunscritos convergen a la llamada constante de circunscripción poligonal

$${\ displaystyle \ prod _ {n = 3} ^ {\ infty} {\ frac {1} {\ cos \ left ({\ frac {\ pi} {n}} \ right)}} = 8.7000366 \ ldots.}

(secuencia A051762 en el OEIS ). El recíproco de esta constante es la constante Kepler-Bouwkamp .