Identidades Fundamentales Altas
Las identidades recíprocas [ editar ]




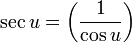

Identidades pitagóricas [ editar ]


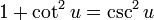
Cociente Identidades [ editar ]
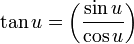

Identidades Co-Function [ editar ]


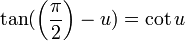



Identidades par-impar [ editar ]






Producto de
Fórmulas [ editar ]
Factores de polinomios Informática requiere el conocimiento de las diferentes fórmulas y un poco de experiencia para saber qué fórmula que se aplica. A continuación, le damos algunas fórmulas importantes:




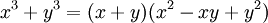

Ejemplos: [ editar ]
::





::
:
:




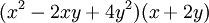

::
:
:
:
:
:
:
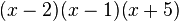

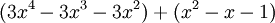


::
:
:

(Nombre thorem)
escribir los coeficientes y si al final es igual a cero, de lo que es una raíz
ejemplo: 


Factores posibles [ editar ]
Para el factor primero debemos buscar posibles factores. Factores posibles son cualquier número que podría ser un factor. Una vez que tenemos un posible factor luego dividir esa cifra en el número que estamos factoring. Si se dividen por igual, entonces tenemos un factor! El factor es la posible factor que encontramos y el resultado de la división. He aquí un ejemplo. Digamos que el número que estamos factoring es 20. 2 es el factor posible. 20/2 = 10. Se reparten uniformemente que significa que tenemos un factor. Los factores son 2 (el factor posible), y 10 (el resultado de la división problema). Ahora que tenemos un factor que empezar de nuevo con un nuevo factor posible y encontrar todos los factores.
Ejemplos [ editar ]
Factor 12
Primera lista de los posibles factores
Los posibles factores son 1,2,3,4,5,6,7,8,9,10,11 y 12
próxima trataremos uno por uno
12/1 = 12 (1 y 12 son factores)
12/2 = 6 (2 y 6 son factores)
12/3 = 4 (3 y 4 son factores)
12/4 = 3 (que ya tenemos los factores 3 y 4)
Una vez que tengamos un factor que ya tenemos a continuación, sabemos que tenemos todos los factores.
Así que los factores de 12 son 1, 2, 3, 4, 6, y 12.
Factor 54
Primera lista de los posibles factores
Los posibles factores son {1, 2, 3 ... 52, 53, 54}
No se preocupe esto no es tanto trabajo como parece!
54/1 = 54 (1 y 54 son factores)
54/2 = 27 (2 y 27 son factores)
54/3 = 18 (3 y 18 son factores)
54/4 = 13r2 (4 no es un factor)
54/5 = 10r4 (5 no es un factor)
54/6 = 9 (6 y 9 son factores)
54/7 = 7R5 (7 no es un factor)
54/8 = 6r6 (8 no es un factor)
54/9 = 6 (que ya tenemos los factores 9 y 6)
Así que los factores de 54 son 1, 2, 3, 6, 9, 18, 27, y 54
Dividir polinomios [ editar ]
El proceso de factoring requerirá dividir polinomios. Esta forma de división no es demasiado diferente de método de división larga, y se conoce como división sintética .
Considere el polinomio x ^ 3 - 21x ^ 2 + 143x - 315. En este caso, los factores determinantes pueden requerir prueba y error (hasta que aprenda las técnicas alternativas), y cuando lo hace, tendrá que dividir el polinomio con el descubierto factor.
En este ejemplo, vamos a dividir por (x-5). La división completa comienza así:
1x -5 | 1x ^ 3 -21x ^ 2 + 143x - 315
Al igual que con la división larga, tiene que encontrar el número que se utiliza para la resta y colocarlo en la parte superior - en este caso, es necesario asegurarse de que el extremo izquierdo plazo se convierte en cero. A continuación, multiplique el top-más plazo que acaba de agregar a la izquierda para obtener la cantidad a restar y realizar la resta.
1x ^ 2
1x -5 | 1x ^ 3 -21x ^ 2 + 143x - 315
1x ^ 3 ^ 2 -5x
------------
-16x ^ 2 + 143x - 315
Repita hasta que la división es completa:
1x ^ 2 -16x + 63
1x -5 | 1x ^ 3 -21x ^ 2 + 143x - 315
1x ^ 3 ^ 2 -5x
------------
-16x ^ 2 + 143x - 315
-16x ^ 2 + 80x
-------------
63x - 315
63x - 315
---------
0
(Si hay un resto en este punto, lo coloca como el numerador en el plazo siendo un factor fuera.)
Algunas personas pueden encontrar escribiendo los x ^ 3 y otras variables a ser voluminosos - si escrito en lápiz y papel, pueden ser omitidos, como parte de la taquigrafía.
1 -16 + 63
1 -5 | 1 -21 143-315
15
-----
-16 143-315
-16 + 80
---------
63-315
63-315
--------
0
En este caso, el factoring es recta hacia adelante ya que se puede determinar fácilmente la cantidad que se utilizará para el siguiente paso en la división.Fórmulas Sum
![sin (u) pecado (v) = \ frac {1} {2} [cos (uv) -cos (u + v)]](https://upload.wikimedia.org/math/3/e/1/3e1d790131330eacb3b4f41156c2fb04.png)
![cos (u) cos (v) = \ frac {1} {2} [cos (uv) + cos (u + v)]](https://upload.wikimedia.org/math/c/b/4/cb427d6ec145056f9eacbdd95b0858a9.png)
![sin (u) cos (v) = \ frac {1} {2} [sin (u + v) + sen (uv)]](https://upload.wikimedia.org/math/d/8/c/d8c59edc56434aba548220a03617614a.png)
![cos (u) pecado (v) = \ frac {1} {2} [sin (u + v) -sen (uv)]](https://upload.wikimedia.org/math/7/0/8/708eacbe9d54efc00b79fdb08897036e.png)
Suma a la Fórmula Producto
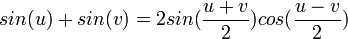

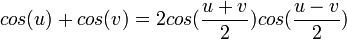
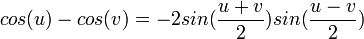
Al graficar las funciones trigonométricas inversas, nos encontramos con un problema. Funciona sólo pueden tener una salida para cada entrada. No encontramos este problema en las funciones trigonométricas ordinarias. Por ejemplo,
sen (θ) = x °, en el que cualquier valor de theta (θ) tendrá exactamente una salida, x grados. Tenga en cuenta que las entradas ocasionales de la función seno producirán la misma salida. Por ejemplo,
sen (90) = sin (450) = sin (810) = 1
Tanto el pecado y el coseno rendirán el mismo de salida después de 360 grados o en radianes 2π, se añade a la de entrada. Las otras cuatro funciones (TAN, cuna, sec, CSC) tienen la misma salida después de una adición de 180 ° o π.
Tenga en cuenta que este mantiene con la definición de una función, en la que cada entrada tiene una sola salida, incluso si el resultado puede ser el mismo para diferentes entradas. Esto no es cierto con las funciones trigonométricas inversas!
arcsen (1) = {90, 450, 810, ..., 90 + n · 360} y así sucesivamente. Por lo tanto, el consenso general es definir simplemente el dominio (entrada) de arcsin entre -90 ° a 90 °, o -π / 2 y π / 2. Del mismo modo, tangente también se define de esta manera. Coseno, por otro lado, tiene su dominio definido entre 0 y π.
Esto se puede ver más fácilmente con una calculadora.
El arcsen (1) = {90 + n · 360} donde n es cualquier valor entero. Sin embargo, la calculadora sólo mostrará los valores "aceptados" entre -90 ° y 90 °. Del mismo modo,
arccos (1) = {n · 360}. Como antes, la calculadora mostrará sólo los valores aceptados entre 0 ° y 180 °.