LISTAS DE FORMAS - TRIÁNGULOS

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Dos triángulos rectángulos con los dos lados del superior igual al lado y la hipotenusa del inferior. De acuerdo a derecha teorema de Fermat triángulo, no es posible para todos los cuatro longitudes de un , b , c , y d que ser enteros.

El teorema del triángulo rectángulo de Fermat es una prueba de no existencia en la teoría de números , la única prueba completa dejada por Pierre de Fermat . ^[1] [2] Tiene varias formulaciones equivalentes:

• Si tres números cuadrados forman una progresión aritmética , la brecha entre los números consecutivos en la progresión (llamada congruum ) no puede ser cuadrada.
• No existen dos triángulos pitagóricos en los que las dos patas de un triángulo sean la pata y la hipotenusa del otro triángulo.
• Un triángulo rectángulo para el cual las tres longitudes de los lados son números racionales no puede tener un área que sea el cuadrado de un número racional. Un área definida de esta manera se llama un número congruente , por lo que ningún número congruente puede ser cuadrado.
• Un triángulo rectángulo y un cuadrado con áreas iguales no pueden tener todos los lados proporcionales entre sí.
• Los únicos puntos racionales en la curva elíptica. $${\ displaystyle y ^ {2} = x (x-1) (x + 1)} son los tres puntos triviales (0,0), (1,0) y (−1,0).
• La ecuación diofantina $${\ displaystyle x ^ {4} -y ^ {4} = z ^ {2}} no tiene solución entera.

Una consecuencia inmediata de la última de estas formulaciones es que el último teorema de Fermat es verdadero para el exponente$${\ displaystyle n = 4,} y por lo tanto para cualquier múltiplo de 4.

Formulación [ editar ]

Cuadrados en progresión aritmética [ editar ]

En 1225, Fibonacci tuvo el desafío de encontrar una construcción para triples de números cuadrados que estén igualmente espaciados entre sí, formando una progresión aritmética , y para el espacio entre estos números, que él llamó un congruum . ^[3] Una forma de describir la solución de Fibonacci es que los números al cuadrado son la diferencia de las patas, la hipotenusa y la suma de las patas de un triángulo pitagórico , y que el congruum es cuatro veces el área del mismo triángulo. ^[4] En su trabajo posterior sobre el problema del congruum, publicado en The Book of Squares, Fibonacci observó que es imposible que un congruum sea un número cuadrado en sí mismo, pero no presentó una prueba satisfactoria de este hecho. ^[5] [6]

Si tres cuadrados $${\ displaystyle a ^ {2}}, $${\ displaystyle b ^ {2}}y $${\ displaystyle c ^ {2}} podría formar una progresión aritmética cuyo congruum también era un cuadrado $${\ displaystyle d ^ {2}}, entonces estos números satisfarían las ecuaciones de Diophantine

$${\ displaystyle a ^ {2} + d ^ {2} = b ^ {2}} y $${\ displaystyle b ^ {2} + d ^ {2} = c ^ {2}}.

Es decir, según el teorema de Pitágoras , formarían dos triángulos rectángulos enteros en los que el par$${\ displaystyle (d, b)}da una pata y la hipotenusa del triángulo más pequeño y el mismo par también forma las dos patas del triángulo más grande. Pero si (como afirmó Fibonacci) no puede existir un congruum cuadrado, entonces no puede haber dos triángulos rectángulos enteros que compartan dos lados de esta manera. ^[7]

Áreas de triángulos rectángulos [ editar ]

Debido a que los congrua son exactamente los números que son cuatro veces el área de un triángulo pitagórico, y la multiplicación por cuatro no cambia si un número es cuadrado, la existencia de un congruum cuadrado es equivalente a la existencia de un triángulo pitagórico con un área cuadrada . Es esta variante del problema lo que concierne a la prueba de Fermat: muestra que no existe tal triángulo. ^[1] Al considerar este problema, Fermat no se inspiró en Fibonacci sino en una edición de Diophantus publicada por Claude Gaspard Bachet de Méziriac . ^[1] Este libro describió varios triángulos rectángulos especiales cuyas áreas tenían formas relacionadas con cuadrados, pero no consideró el caso de áreas que eran en sí mismas cuadradas. ^[8]

Al reorganizar las ecuaciones para los dos triángulos pitagóricos anteriores, y luego multiplicarlos juntos, se obtiene la ecuación única de Diofantina

$${\ displaystyle b ^ {4} -d ^ {4} = (b ^ {2} -d ^ {2}) (b ^ {2} + d ^ {2}) = a ^ {2} c ^ { 2}}

que se puede simplificar a

$${\ displaystyle b ^ {4} -d ^ {4} = e ^ {2}.}

Por el contrario, cualquier solución a esta ecuación podría factorizarse para dar un congruum cuadrado. (En particular, los cuadrados$${\ displaystyle (b ^ {4} -d ^ {4} -2b ^ {2} d ^ {2}) ^ {2}}, $${\ displaystyle (b ^ {4} + d ^ {4}) ^ {2}}y $${\ displaystyle (b ^ {4} -d ^ {4} + 2b ^ {2} d ^ {2}) ^ {2}} formar una progresión aritmética con congruum $${\ displaystyle 4b ^ {2} d ^ {2} (b ^ {4} -d ^ {4}) = (2bde) ^ {2}}, que es un cuadrado en sí mismo.) Por lo tanto, la solubilidad de esta ecuación es equivalente a la existencia de un congruum cuadrado. Pero, si el último teorema de Fermat fuera falso para el exponente$${\ displaystyle n = 4}, luego cuadrar uno de los tres números en cualquier contraejemplo también daría tres números que resuelven esta ecuación. Por lo tanto, la prueba de Fermat de que ningún triángulo pitagórico tiene un área cuadrada implica que esta ecuación no tiene solución, y que este caso del último teorema de Fermat es verdadero. ^[8]

Otra formulación equivalente del mismo problema involucra números congruentes , los números que son áreas de triángulos rectángulos cuyos tres lados son todos números racionales . Al multiplicar los lados por un denominador común, cualquier número congruente puede transformarse en el área de un triángulo pitagórico, de donde se deduce que los números congruentes son exactamente los números formados al multiplicar un congruum por el cuadrado de un número racional. Por lo tanto, no hay congruum cuadrado si y solo si el número 1 no es un número congruente. ^{[9] [10] De manera} equivalente, es imposible que un cuadrado (la forma geométrica) y un triángulo rectángulo tengan áreas iguales y todos los lados proporcionalesjuntos. ^[6]

Curva elíptica [ editar ]

Otra forma equivalente del teorema de Fermat implica la curva elíptica que consiste en los puntos cuyas coordenadas cartesianas $${\ displaystyle (x, y)} satisfacer la ecuación

$${\ displaystyle y ^ {2} = x (x + 1) (x-1).}

Esta ecuación tiene los pares obvios de soluciones (0,0), (1,0) y (−1,0). El teorema de Fermat es equivalente a la afirmación de que estos son los únicos puntos en la curva para los cuales x e y son racionales. ^[10] [11]

La prueba de Fermat [ editar ]

Durante su vida, Fermat desafió a varios otros matemáticos a probar la inexistencia de un triángulo pitagórico con área cuadrada, pero no publicó la prueba por sí mismo. Sin embargo, escribió una prueba en su copia de Bachet's Diophantus, que su hijo descubrió y publicó póstumamente. ^{[1] [6] [12]}

La prueba de Fermat es una prueba de descendencia infinita . Muestra que, de cualquier ejemplo de un triángulo pitagórico con área cuadrada, se puede obtener un ejemplo más pequeño. Dado que los triángulos pitagóricos tienen áreas enteras positivas y no existe una secuencia descendente infinita de enteros positivos, tampoco puede existir un triángulo pitagórico con área cuadrada. ^[1] [6]

Con más detalle, supongamos que $${\ displaystyle x}, $${\ displaystyle y}y $${\ displaystyle z}son los lados enteros de un triángulo rectángulo con área cuadrada. Al dividir por cualquier factor común, se puede suponer que este triángulo es primitivo ^[6] y de la forma conocida de todos los triples pitagóricos primitivos, se puede establecer$${\ displaystyle x = 2pq}, $${\ displaystyle y = p ^ {2} -q ^ {2}}y $${\ displaystyle z = p ^ {2} + q ^ {2}}, por el cual el problema se transforma en encontrar enteros relativamente primos $${\ displaystyle p} y $${\ displaystyle q} (uno de los cuales es par) tal que $${\ displaystyle pq (p ^ {2} -q ^ {2})}es cuadrado Los cuatro factores lineales.$${\ displaystyle p}, $${\ displaystyle q}, $${\ displaystyle p + q}y $${\ displaystyle pq}son relativamente primos y, por lo tanto, deben ser cuadrados; dejar$${\ displaystyle p + q = r ^ {2}} y $${\ displaystyle pq = s ^ {2}}. Ambos$${\ displaystyle r} y $${\ displaystyle s} debe ser extraño ya que exactamente uno de $${\ displaystyle p} o $${\ displaystyle q}es par y el otro es impar. Por lo tanto, ambos$${\ displaystyle rs} y $${\ displaystyle r + s} son pares, uno de los cuales es divisible por 4. De estos dos números, Fermat deriva dos números más $${\ displaystyle u = (rs) / 2} y $${\ displaystyle v = (r + s) / 2}, uno de los cuales es incluso por la oración anterior. Porque$${\ displaystyle u ^ {2} + v ^ {2} = p} es un cuadrado $${\ displaystyle u} y $${\ displaystyle v} son las patas de otro triángulo pitagórico primitivo cuya área $${\ displaystyle (uv) / 2 = q / 4}. Ya que$${\ displaystyle q} es en sí mismo un cuadrado y desde $${\ displaystyle uv} incluso, $${\ displaystyle q / 4}Es un cuadrado. Por lo tanto, cualquier triángulo pitagórico con área cuadrada conduce a un triángulo pitagórico más pequeño con área cuadrada, completando la prueba.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Círculo de Fuhrmann

Círculo de Fuhrmann con triángulo de Fuhrmann (rojo),
punto Nagel$${\ displaystyle N} y ortocentro $${\ displaystyle H}
$${\ displaystyle | AP_ {a} | = BP_ {b} | = | CP_ {c} | = 2r}

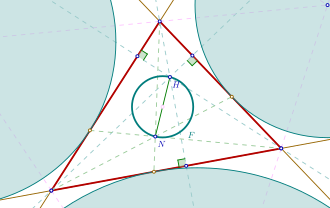
En geometría , el círculo de un triángulo de Fuhrmann , llamado así por el alemán Wilhelm Fuhrmann (1833–1904), es el círculo con un diámetro del segmento de línea entre el ortocentro $${\ displaystyle H}y el punto Nagel $${\ displaystyle N}. Este círculo es idéntico al círculo del triángulo de Fuhrmann . ^[1]

El radio del círculo Fuhrmann de un triángulo con lados un , b , y c y circunradio R es

$${\ displaystyle R {\ sqrt {\ frac {a ^ {3} -a ^ {2} b-ab ^ {2} + b ^ {3} -a ^ {2} c + 3abc-b ^ {2} c-ac ^ {2} + c ^ {3}} {abc}}},}

que también es la distancia entre el circuncentro y el incentro . ^[2]

Al lado del ortocentro, el círculo de Fuhrmann cruza cada altitud del triángulo en un punto adicional. Todos esos puntos tienen la distancia.$${\ displaystyle 2r}de sus vértices asociados del triángulo. aquí$${\ displaystyle r}denota el radio del triángulo incircle . 

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Triángulo de Fuhrmann (rojo): $${\ displaystyle \ triangle M_ {c} ^ {\ prime} M_ {b} ^ {\ prime} M_ {a} ^ {\ prime}}
puntos de arco medio: $${\ displaystyle M_ {a}, M_ {b}, M_ {c}}

Triángulo de Fuhrmann (rojo): $${\ displaystyle \ triangle M_ {c} ^ {\ prime} M_ {b} ^ {\ prime} M_ {a} ^ {\ prime}}
$${\ displaystyle \ triangle M_ {c} ^ {\ prime} M_ {b} ^ {\ prime} M_ {a} ^ {\ prime} \ sim \ triangle M_ {a} M_ {b} M_ {c}}

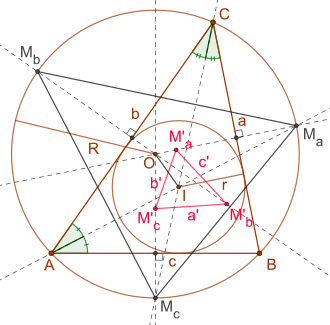
El triángulo de Fuhrmann , llamado así por Wilhelm Fuhrmann (1833–1904), es un triángulo especial basado en un triángulo arbitrario dado.

Para un triángulo dado $${\ displaystyle \ triangle ABC}y su circunferencia circunda los puntos medios de los arcos sobre los lados del triángulo se denotan por $${\ displaystyle M_ {a}, M_ {b}, M_ {c}}. Esos puntos medios se reflejan en los lados del triángulo asociado, produciendo los puntos.$${\ displaystyle M_ {a} ^ {\ prime}, M_ {b} ^ {\ prime}, M_ {c} ^ {\ prime}}, que forma el triángulo de Fuhrmann . ^[1] [2]

La circunferencia del triángulo de Fuhrmann es el círculo de Fuhrmann . Además, el triángulo de Furhmann es similar al triángulo formado por los puntos del arco medio, es decir$${\ displaystyle \ triangle M_ {c} ^ {\ prime} M_ {b} ^ {\ prime} M_ {a} ^ {\ prime} \ sim \ triangle M_ {a} M_ {b} M_ {c}}. ^[1] Para el área del triángulo de Fuhrmann se cumple la siguiente fórmula: ^[3]

$${\ displaystyle | \ triangle M_ {c} ^ {\ prime} M_ {b} ^ {\ prime} M_ {a} ^ {\ prime} | = {\ frac {(a + b + c) | OI | ^ {2}} {4R}} = {\ frac {(a + b + c) (R-2r)} {4}}}

Dónde $${\ displaystyle O} denota el circuncentro del triángulo dado $${\ displaystyle \ triangle ABC} y $${\ displaystyle R} su radio así como $${\ displaystyle I} denotando el incentro y $${\ displaystyle r}su radio Debido al teorema de Euler, uno también tiene $${\ displaystyle | OI | ^ {2} = R (R-2r)}. Las siguientes ecuaciones son válidas para los lados del triángulo de Fuhrmann: ^[3]

$${\ displaystyle a ^ {\ prime} = {\ sqrt {\ frac {(-a + b + c) (a + b + c)} {bc}}} | OI |}

$${\ displaystyle b ^ {\ prime} = {\ sqrt {\ frac {(a-b + c) (a + b + c)} {ac}}} | OI |}

$${\ displaystyle c ^ {\ prime} = {\ sqrt {\ frac {(a + bc) (a + b + c)} {ab}}} | OI |}

Dónde $${\ displaystyle a, b, c} denotar los lados del triángulo dado $${\ displaystyle \ triangle ABC} y $${\ displaystyle a ^ {\ prime}, b ^ {\ prime}, c ^ {\ prime}} los lados del triángulo de Fuhrmann (ver dibujo).