LISTAS DE FORMAS - TRIÁNGULOS

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

triángulo ortico: $${\ displaystyle \ triangle DEF}
triángulos inscritos: $${\ displaystyle \ triangle DEF \ ,, \ triangle GHI}
$${\ displaystyle | DE | + | EF | + | FD | \ leq | GH | + | HI | + | IG |}

En geometría , el problema de Fagnano es un problema de optimización que fue declarado por primera vez por Giovanni Fagnano en 1775:

Para un triángulo agudo determinado , determine el triángulo inscrito de perímetro mínimo .

La solución es el triángulo órtico , con vértices en los puntos base de las altitudes del triángulo dado.

Solución [ editar ]

El triángulo ortico , con vértices en los puntos base de las altitudes del triángulo dado, tiene el perímetro más pequeño de todos los triángulos inscritos en un triángulo agudo, por lo tanto, es la solución del problema de Fagnano. La prueba original de Fagnano utilizó métodos de cálculo y un resultado intermedio dado por su padre Giulio Carlo de 'Toschi di Fagnano . Más tarde, sin embargo, también se descubrieron varias pruebas geométricas, entre otras por Hermann Schwarz y Lipót Fejér . Estas pruebas utilizan las propiedades geométricas de los reflejos para determinar un camino mínimo que representa el perímetro.

Principios físicos [ editar ]

Se encuentra una solución de la física imaginando poner una banda elástica que sigue la Ley de Hooke alrededor de los tres lados de un marco triangular$${\ displaystyle ABC}, de modo que pueda deslizarse suavemente. Luego, la banda elástica terminaría en una posición que minimiza su energía elástica y, por lo tanto, minimiza su longitud total. Esta posición da el triángulo perimetral mínimo. La tensión dentro de la banda elástica es la misma en todas partes en la banda elástica, por lo que, en su posición de reposo, tenemos, según el teorema de Lami ,$${\ displaystyle \ angle bcA = \ angle acB, \ angle caB = \ angle baC, \ angle abC = \ angle cbA}

Triangle abc es el triángulo ortético del triángulo ABC

Por lo tanto, este triángulo mínimo es el triángulo ortico.

punto Fermat de un triángulo , también llamado punto Torricelli o punto Fermat-Torricelli , es un punto tal que la distancia total desde los tres vértices del triángulo al punto es la mínima posible. ^[1] Se llama así porque Fermat planteó este problema por primera vez en una carta privada dirigida a Evangelista Torricelli , quien lo resolvió.

El punto de Fermat da una solución a la mediana geométrica y los problemas del árbol de Steiner para tres puntos.

Fig. 1. Construcción del primer centro isogónico, X (13). Cuando ningún ángulo del triángulo excede los 120 °, este punto es el punto de Fermat.

Construcción [ editar ]

El punto de Fermat de un triángulo con el ángulo más grande como máximo 120 ° es simplemente su primer centro isogónico o X (13) , que se construye de la siguiente manera:

1. Construya un triángulo equilátero en cada uno de los dos lados elegidos arbitrariamente del triángulo dado.
2. Dibuja una línea desde cada vértice nuevo hasta el vértice opuesto del triángulo original.
3. Las dos líneas se cruzan en el punto de Fermat.

Un método alternativo es el siguiente:

1. En cada uno de los dos lados elegidos arbitrariamente, construya un triángulo isósceles , con la base del lado en cuestión, ángulos de 30 grados en la base y el tercer vértice de cada triángulo isósceles que se encuentra fuera del triángulo original.
2. Para cada triángulo isósceles dibuje un círculo, en cada caso con el centro en el nuevo vértice del triángulo isósceles y con un radio igual a cada uno de los dos lados nuevos de ese triángulo isósceles.
3. La intersección dentro del triángulo original entre los dos círculos es el punto de Fermat.

Cuando un triángulo tiene un ángulo mayor de 120 °, el punto de Fermat se ubica en el vértice de ángulo obtuso.

En lo que sigue "Caso 1" significa que el triángulo tiene un ángulo superior a 120 °. "Caso 2" significa que ningún ángulo del triángulo excede los 120 °.

Ubicación de X (13) [ editar ]

Fig. 2. Geometría del primer centro isogónico.

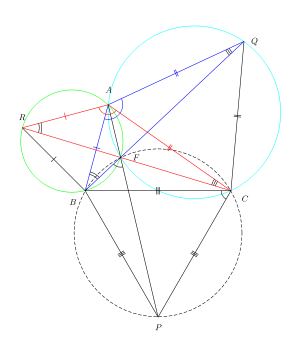
La figura 2 muestra los triángulos equiláteros ARB, AQC y CPB unidos a los lados del triángulo arbitrario ABC. Aquí hay una prueba que usa las propiedades de los puntos concíclicos para mostrar que las tres líneas RC, BQ y AP en la Fig. 2 se cruzan en el punto F y se cortan entre sí en ángulos de 60 °.

Los triángulos RAC y BAQ son congruentes porque el segundo es una rotación de 60 ° del primero sobre A. Por lo tanto, ∠ARF = ∠ABF y ∠AQF = ∠ACF. Por el contrario del teorema del ángulo inscrito aplicado al segmento AF, los puntos ARBF son concíclicos (se encuentran en un círculo). Del mismo modo, los puntos AFCQ son concíclicos.

∠ARB = 60 °, entonces ∠AFB = 120 °, usando el teorema del ángulo inscrito . Del mismo modo, ∠AFC = 120 °.

Entonces ∠BFC = 120 °. Entonces, ∠BFC y ∠BPC suman 180 °. Usando el teorema del ángulo inscrito , esto implica que los puntos BPCF son concíclicos. Entonces, usando el teorema del ángulo inscrito aplicado al segmento BP, ∠BFP = ∠BCP = 60 °. Como ∠BFP + ∠BFA = 180 °, el punto F se encuentra en el segmento de línea AP. Entonces, las líneas RC, BQ y AP son concurrentes (se cruzan en un solo punto). QED

Esta prueba se aplica solo en el Caso 2 ya que si ∠BAC> 120 °, el punto A se encuentra dentro del círculo de BPC que cambia las posiciones relativas de A y F. Sin embargo, se modifica fácilmente para cubrir el Caso 1. Entonces ∠AFB = ∠AFC = 60 ° por lo tanto ∠BFC = ∠AFB = ∠AFC = 120 °, lo que significa que BPCF es cíclico, por lo que ∠BFP = ∠BCP = 60 ° = ∠BFA. Por lo tanto, A se encuentra en FP.

Las líneas que unen los centros de los círculos en la figura 2 son perpendiculares a los segmentos de línea AP, BQ y CR. Por ejemplo, la línea que une el centro del círculo que contiene ARB y el centro del círculo que contiene AQC, es perpendicular al segmento AP. Entonces, las líneas que unen los centros de los círculos también se cruzan en ángulos de 60 °. Por lo tanto, los centros de los círculos forman un triángulo equilátero. Esto se conoce como el teorema de Napoleón .

Ubicación del punto de Fermat [ editar ]

Geometría tradicional [ editar ]

Fig 3. Geometría del punto Fermat

Dado cualquier triángulo euclidiano ABC y un punto arbitrario P sea d (P) = PA + PB + PC, con PA que denota la distancia entre P y A. El objetivo de esta sección es identificar un punto P ₀ tal que d (P ₀ ) ₀ . Si tal punto existe, entonces será el punto de Fermat. En lo que sigue, Δ denotará los puntos dentro del triángulo y se tomará para incluir su límite Ω.

Un resultado clave que se utilizará es la regla dogleg que afirma que si un triángulo y un polígono tienen un lado en común y el resto del triángulo se encuentra dentro del polígono, entonces el triángulo tiene un perímetro más corto que el polígono.
[Si AB es el lado común, extienda AC para cortar el polígono en X. Luego, por la desigualdad del triángulo, el perímetro del polígono> AB + AX ​​+ XB = AB + AC + CX + XB ≥ AB + AC + BC.]

Sea P cualquier punto fuera de Δ. Asocia cada vértice con su zona remota; es decir, el semiplano más allá del lado opuesto (extendido). Estas 3 zonas cubren todo el plano, excepto Δ y P se encuentra claramente en una o dos de ellas. Si P está en dos (digamos la intersección de las zonas B y C), entonces establecer P '= A implica d (P') = d (A) Alternativamente, si P está en una sola zona, diga la zona A, entonces d (P ') Entonces, para cada punto P fuera de Δ existe un punto P 'en Ω tal que d (P')  .

Caso 1. El triángulo tiene un ángulo ≥ 120 °.

Sin pérdida de generalidad, suponga que el ángulo en A es ≥ 120 °. Construya el triángulo equilátero AFB y para cualquier punto P en Δ (excepto A) construya Q de manera que el triángulo AQP sea equilátero y tenga la orientación mostrada. Entonces el triángulo ABP es una rotación de 60 ° del triángulo AFQ sobre A, por lo que estos dos triángulos son congruentes y se deduce que d (P) = CP + PQ + QF, que es simplemente la longitud de la ruta CPQF. Como P está restringido a estar dentro de ABC, por la regla dogleg la longitud de esta ruta excede AC + AF = d (A). Por lo tanto, d (A) Desde arriba, existe un punto P 'є Ω tal que d (P') Por lo tanto, d (A) En otras palabras,el punto de Fermat se encuentra en el vértice de ángulo obtuso .

Caso 2. El triángulo no tiene ángulo ≥ 120 °.

Construya el triángulo equilátero BCD y deje que P sea cualquier punto dentro de Δ y construya el triángulo equilátero CPQ. Entonces CQD es una rotación de 60 ° de CPB sobre C, entonces d (P) = PA + PB + PC = AP + PQ + QD, que es simplemente la longitud del camino APQD. Deje P ₀ ser el punto donde AD y CF se cruzan. Este punto se llama comúnmente el primer centro isogónico. Realice el mismo ejercicio con P ₀ que hizo con P y encuentre el punto Q ₀ . Por la restricción angular P _{0 se} encuentra dentro de Δ además BCF es una rotación de 60 ° de BDA alrededor de B, por lo que Q ₀ debe estar en algún lugar de AD. Como CDB = 60 ° se deduce que Q _{0 se} encuentra entre P ₀ y D, lo que significa AP ₀ Q ₀D es una línea recta, entonces d (P ₀ ) = AD. Además, si P ≠ P ₀ , P o Q no estarán en AD, lo que significa d (P ₀ ) = AD Ahora permita que P se extienda fuera de Δ. Desde arriba, existe un punto P 'є Ω tal que d (P') ₀ ) ≤ d (P ') se deduce que d (P ₀ ) Eso significa que P ₀ es el punto de Fermat de Δ. En otras palabras, el punto de Fermat coincide con el primer centro isogónico .

Análisis vectorial [ editar ]

Deje que O , A , B , C , X sean cinco puntos en un plano. Denota los vectores${\displaystyle {\overrightarrow {\mathrm {OA} }},{\overrightarrow {\mathrm {OB} }},{\overrightarrow {\mathrm {OC} }},{\overrightarrow {\mathrm {OX} }}}$por a , b , c , x respectivamente, y sea i , j , k los vectores unitarios de O a lo largo de a , b , c .
Ahora | a | = a⋅i = ( a - x ) ⋅i + x⋅i ≤ | a - x | + x⋅i y similar | b | ≤ | b - x | + x⋅j y | c | ≤ |c - x | + x⋅k .
Agregar da | a | + | b | + | c | ≤ | a - x | + | b - x | + | c - x | + x⋅ ( i + j + k ).
Si a , b , c se encuentran en O en ángulos de 120 °, entonces i + j + k = 0, entonces | a | + | siEl | + | c | ≤ | a - x | + | b - x | + | c - x | para todo x .
En otras palabras, OA + OB + OC ≤ XA + XB + XC y, por lo tanto, O es el punto de Fermat de ABC .
Este argumento falla cuando el triángulo tiene un ángulo ∠C > 120 ° porque no hay un punto O donde a , b , creunirse en ángulos de 120 °. Sin embargo, se soluciona fácilmente redefiniendo k = - ( i + j ) y colocando O en C para que c = 0 . Tenga en cuenta que | k | ≤ 1 porque el ángulo entre los vectores unitarios i y j es ∠C que excede los 120 °. Desde | 0 | ≤ | 0 - x | + x⋅k la tercera desigualdad aún se mantiene, las otras dos desigualdades no cambian. La prueba ahora continúa como anteriormente (sumando las tres desigualdades y usando i + j +k = 0 ) para llegar a la misma conclusión de que O (o en este caso C ) debe ser el punto de Fermat de ABC .

Multiplicadores de Lagrange [ editar ]

Otro enfoque para encontrar un punto dentro del triángulo, desde donde la suma de las distancias a los vértices del triángulo es mínima, es usar uno de los métodos de optimización (matemática) . En particular, método de los multiplicadores de Lagrange y la ley de cosenos .

Dibujamos líneas desde el punto dentro del triángulo de sus vértices y los llamamos X , Y y Z . Además, deje que las longitudes de estas líneas sean x, y y z, respectivamente. Deje que el ángulo entre X e Y sea ​​α, Y y Z sea ​​β. Entonces el ángulo entre X y Z es (2π - α - β). Usando el método de multiplicadores de Lagrange, tenemos que encontrar el mínimo de la L de Lagrange , que se expresa como:

L = x + y + z + λ ₁ ( x ² + y ² - 2 xy cos ( α ) - a ² ) + λ ₂ ( y ² + z ² - 2 yz cos (β) - b ² ) + λ ₃ ( z ² + x ² - 2 zx cos ( α + β ) - c ² )

donde una , b y c son las longitudes de los lados del triángulo.

Al igualar cada una de las cinco derivadas parciales δ L / δx, δ L / δy, δ L / δz, δ L / δα, δ L / δβ a cero y eliminar λ ₁ , λ ₂ , λ ₃ finalmente da sin (α) = sin (β) y sin (α + β) = - sin (β), entonces α = β = 120 °. Sin embargo, la eliminación es un asunto largo y tedioso, y el resultado final cubre solo el Caso 2.

Propiedades [ editar ]

Los dos centros isogónicos son las intersecciones de tres vesicas piscis cuyos vértices emparejados son los vértices del triángulo.

• Cuando el ángulo más grande del triángulo no es mayor que 120 °, X (13) es el punto de Fermat.
• Los ángulos subtendidos por los lados del triángulo en X (13) son todos iguales a 120 ° (Caso 2), o 60 °, 60 °, 120 ° (Caso 1).
• Los círculos de los tres triángulos equiláteros construidos son concurrentes en X (13).
• Coordenadas trilineales para el primer centro isogónico, X (13):

csc ( A + π / 3): csc ( B + π / 3): csc ( C + π / 3), o, de manera equivalente,

sec ( A - π / 6): sec ( B - π / 6): sec ( C - π / 6). ^[2]

• Coordenadas trilineales para el segundo centro isogónico, X (14):

csc ( A - π / 3): csc ( B - π / 3): csc ( C - π / 3), o, de manera equivalente,

seg ( A + π / 6): seg ( B + π / 6): seg ( C + π / 6). ^[3]

• Coordenadas trilineales para el punto de Fermat:

1 - u + uvw sec ( A - π / 6): 1 - v + uvw sec ( B - π / 6): 1 - w + uvw sec ( C - π / 6)

donde u, v, w denotan respectivamente las variables booleanas ( A <120 font="" nbsp="">B <120 font="" nbsp="">C <120 font="">

• El conjugado isogonal de X (13) es el primer punto isodinámico , X (15):

sin ( A + π / 3): sin ( B + π / 3): sin ( C + π / 3). ^[4]

• El conjugado isogonal de X (14) es el segundo punto isodinámico , X (16):

sin ( A - π / 3): sin ( B - π / 3): sin ( C - π / 3). ^[5]

• Los siguientes triángulos son equiláteros:

triángulo antipedal de X (13)

triángulo antipedal de X (14)

triángulo de pedal de X (15)

triángulo de pedal de X (16)

triángulo circunceviano de X (15)

triángulo circunceviano de X (16)

• Las líneas X (13) X (15) y X (14) X (16) son paralelas a la línea de Euler . Las tres líneas se encuentran en el punto infinito de Euler, X (30).
• Los puntos X (13), X (14), el circuncentro y el centro de nueve puntos se encuentran en un círculo de Lester .
• La línea X (13) X (14) se encuentra con la línea de Euler en el punto medio de X (2) y X (4). ^[6]
• El punto de Fermat se encuentra en el disco ortocentroidal abierto perforado en su propio centro, y podría ser cualquier punto en él. ^[7]

Alias [ editar ]

Los centros isogónicos X (13) y X (14) también se conocen como el primer punto de Fermat y el segundo punto de Fermat, respectivamente. Las alternativas son el punto de Fermat positivo y el punto de Fermat negativo . Sin embargo, estos nombres diferentes pueden ser confusos y quizás sea mejor evitarlos. El problema es que gran parte de la literatura difumina la distinción entre el punto de Fermat y el primer punto de Fermat, mientras que solo en el caso 2 anterior son en realidad los mismos.

Historia [ editar ]

Esta pregunta fue propuesta por Fermat, como un desafío para Evangelista Torricelli . Resolvió el problema de manera similar a la de Fermat, aunque en su lugar usó la intersección de los círculos de los tres triángulos regulares. Su alumno, Viviani, publicó la solución en 1659.