En geometría , el punto de un triángulo de Longchamps es un centro triangular que lleva el nombre del matemático francés Gaston Albert Gohierre de Longchamps . Es el reflejo del ortocentro del triángulo sobre el circuncentro .
Definición [ editar ]
Deje que el triángulo dado tenga vértices , y , frente a los lados respectivos , y , como es la notación estándar en geometría triangular. En el artículo de 1886 en el que introdujo este punto, De Longchamps lo definió inicialmente como el centro de un círculo. ortogonal a los tres círculos , y , dónde está centrado en con radio y los otros dos círculos están definidos simétricamente. De Longchamps también mostró que el mismo punto, ahora conocido como el punto de Longchamps, puede definirse de manera equivalente como el ortocentro del triángulo anticomplementario dey que es el reflejo del ortocentro de alrededor del circuncentro. [2]
El círculo de Steiner de un triángulo es concéntrico con el círculo de nueve puntos y tiene un radio 3/2 del circunradio del triángulo; El punto de Longchamps es el centro homotético del círculo de Steiner y el círculo circunferencial. [3]
Propiedades adicionales [ editar ]
Como el reflejo del ortocentro alrededor del circuncentro, el punto de Longchamps pertenece a la línea a través de ambos puntos, que es la línea de Euler del triángulo dado. Por lo tanto, es colineal con todos los otros centros de triángulos en la línea de Euler, que junto con el ortocentro y el circuncentro incluyen el centroide y el centro del círculo de nueve puntos . [1] [3] [4]
El punto de Longchamp también es colineal, a lo largo de una línea diferente, con el incentro y el punto Gergonne de su triángulo. [1] [5] Los tres círculos centrados en, y , con radios , y respectivamente (donde es el semiperímetro ) son mutuamente tangentes, y hay dos círculos más tangentes a los tres, los círculos internos y externos de Soddy; Los centros de estos dos círculos también se encuentran en la misma línea con el punto de Longchamp y el incentro. [1] [3] El punto de Longchamp es el punto de concurrencia de esta línea con la línea de Euler, y con otras tres líneas definidas de manera similar a la línea a través del incentro pero usando en su lugar los tres excedentes del triángulo. [3] [5]
El cúbico Darboux puede definirse desde el punto de Longchamps, como el lugar geométrico de los puntos. tal que , el conjugado isogonal de, y el punto de De Longchamps son colineales. Es la única curva cúbica invariante de un triángulo que es a la vez autoconjugado isogonalmente y centralmente simétrica; Su centro de simetría es el circuncentro del triángulo. [6] El punto de De Longchamps se encuentra en esta curva, al igual que su reflejo en el ortocentro.
(Redirigido desde el teorema de Desargues )
- Dos triángulos están en perspectiva axialmente si y solo si están en perspectiva centralmente .
Denotan los tres vértices de un triángulo por una , b y c , y los de la otra por A , B y C . La perspectiva axial significa que las líneas ab y AB se encuentran en un punto, las líneas ac y AC se encuentran en un segundo punto, y las líneas bc y BC se encuentran en un tercer punto, y que estos tres puntos se encuentran en una línea común llamada eje de perspectiva . La perspectiva central significa que las tres líneas Aa , Bb yLos CC son concurrentes, en un punto llamadocentro de perspectiva.
Este teorema de intersección es cierto en el plano euclidiano habitual , pero se debe tener especial cuidado en casos excepcionales, como cuando un par de lados son paralelos, de modo que su "punto de intersección" retroceda hasta el infinito. Comúnmente, para eliminar estas excepciones, los matemáticos "completan" el plano euclidiano agregando puntos en el infinito, siguiendo a Jean-Victor Poncelet . Esto da como resultado un plano proyectivo .
El teorema de Desargues es verdadero para el plano proyectivo real , para cualquier espacio proyectivo definido aritméticamente a partir de un campo o anillo de división , para cualquier espacio proyectivo de dimensión desigual a dos, y para cualquier espacio proyectivo en el que se mantenga el teorema de Pappus . Sin embargo, hay muchos planos en los que el teorema de Desargues es falso.
Historia [ editar ]
Desargues nunca publicó este teorema, pero apareció en un apéndice titulado Método universal de M. Desargues para usar la perspectiva ( Manière universelle de M. Desargues pour practiquer la perspective ) a un libro práctico sobre el uso de la perspectiva publicado en 1648 [1] por su amigo y alumno Abraham Bosse (1602–1676). [2]
Espacios proyectivos versus espacios afines [ editar ]
En un espacio afín como el plano euclidiano, una afirmación similar es cierta, pero solo si se enumeran varias excepciones que involucran líneas paralelas. El teorema de Desargues es, por lo tanto, uno de los teoremas geométricos más simples cuyo hogar natural se encuentra en un espacio proyectivo en lugar de afín.
Auto dualidad [ editar ]
Por definición, dos triángulos son en perspectiva si y solo si están en perspectiva centralmente (o, de manera equivalente según este teorema, en perspectiva axialmente). Tenga en cuenta que los triángulos de perspectiva no necesitan ser similares .
Bajo la dualidad estándar de la geometría proyectiva plana (donde los puntos corresponden a las líneas y la colinealidad de los puntos corresponde a la concurrencia de las líneas), la declaración del teorema de Desargues es auto dual: [3] la perspectiva axial se traduce en perspectiva central y viceversa. La configuración de Desargues (a continuación) es una configuración auto dual. [4]
Prueba del teorema de Desargues [ editar ]
El teorema de Desargues se aplica al espacio proyectivo de cualquier dimensión sobre cualquier campo o anillo de división, y también se aplica a los espacios proyectivos abstractos de dimensión al menos 3. En la dimensión 2, los planos para los que se denomina se denominan planos desarguesianos y son los mismos que los planos que se pueden dar coordenadas sobre un anillo de división. También hay muchos planos no desarguesianos donde el teorema de Desargues no es válido.
Prueba tridimensional [ editar ]
El teorema de Desargues es verdadero para cualquier espacio proyectivo de dimensión de al menos 3, y más generalmente para cualquier espacio proyectivo que pueda integrarse en un espacio de dimensión de al menos 3.
El teorema de Desargues puede expresarse de la siguiente manera:
- Si las líneas Aa , Bb y Cc son concurrentes (se encuentran en un punto), entonces
- los puntos AB ∩ ab , AC ∩ ac y BC ∩ bc son colineales .
Los puntos A , B , una y b son coplanares (se encuentran en el mismo plano), debido a la concurrencia supuesta de Aa y Bb . Por lo tanto, las líneas AB y ab pertenecen al mismo plano y deben cruzarse. Además, si los dos triángulos se encuentran en planos diferentes, entonces el punto AB ∩ ab pertenece a ambos planos. Por un argumento simétrico, los puntos AC ∩ ac y BC ∩ bcTambién existen y pertenecen a los planos de ambos triángulos. Como estos dos planos se cruzan en más de un punto, su intersección es una línea que contiene los tres puntos.
Esto prueba el teorema de Desargues si los dos triángulos no están contenidos en el mismo plano. Si están en el mismo plano, el teorema de Desargues se puede probar eligiendo un punto que no esté en el plano, usando esto para levantar los triángulos fuera del plano de modo que el argumento anterior funcione, y luego proyectar nuevamente en el plano. El último paso de la prueba falla si el espacio proyectivo tiene una dimensión inferior a 3, ya que en este caso puede no ser posible encontrar un punto fuera del plano.
El teorema de Monge también afirma que tres puntos se encuentran en una línea, y tiene una prueba que usa la misma idea de considerarlo en tres dimensiones en lugar de dos y escribir la línea como una intersección de dos planos.
Prueba bidimensional [ editar ]
Como hay planos proyectivos no desarguesianos en los que el teorema de Desargues no es verdadero, [5] se deben cumplir algunas condiciones adicionales para demostrarlo. Estas condiciones generalmente toman la forma de suponer la existencia de suficientes colaciones de cierto tipo, lo que a su vez lleva a mostrar que el sistema de coordenadas algebraico subyacente debe ser un anillo de división (campo de inclinación). [6]
Relación con el teorema de Pappus [ editar ]
Teorema del hexágono de Pappus estados que, si un hexágono abcabc se dibuja en una forma tal que los vértices de un , b y c se encuentran en una línea y vértices A , B y C se encuentran en una segunda línea, entonces cada uno de dos lados opuestos del hexágono se encuentran en dos líneas que se encuentran en un punto y los tres puntos construidos de esta manera son colineales. Un plano en el que el teorema de Pappus es universalmente verdadero se llama pappiano . Hessenberg (1905) [7] demostró que el teorema de Desargues puede deducirse de tres aplicaciones del teorema de Pappus. [8]
Lo contrario de este resultado no es cierto, es decir, no todos los planos desarguesianos son papianos. Satisfacer el teorema de Pappus es equivalente a que el sistema de coordenadas subyacente sea conmutativo . Por lo tanto, un plano definido sobre un anillo de división no conmutativo (un anillo de división que no es un campo) sería desarguesiano pero no pappiano. Sin embargo, debido al pequeño teorema de Wedderburn , que establece que todos los anillos de división finita son campos, todos los planos desarguesianos finitos son papianos. No se conoce una prueba completamente geométrica de este hecho, aunque Bamberg y Penttila (2015) brinde una prueba que use solo hechos algebraicos "elementales" (en lugar de la fuerza completa del pequeño teorema de Wedderburn).
La configuración de Desargues [ editar ]
Las diez líneas involucradas en el teorema de Desargues (seis lados de triángulos, las tres líneas Aa , Bb y Cc , y el eje de perspectiva) y los diez puntos involucrados (los seis vértices, los tres puntos de intersección en el eje de perspectiva, y el centro de la perspectiva) están tan dispuestos que cada una de las diez líneas pasa a través de tres de los diez puntos, y cada uno de los diez puntos se encuentra en tres de las diez líneas. Esos diez puntos y diez líneas conforman la configuración de Desargues , un ejemplo de una configuración proyectiva . Aunque el teorema de Desargues elige diferentes roles para estas diez líneas y puntos, la configuración de Desargues en sí es más simétrica : cualquiera de los diez puntos pueden ser elegidos para ser el centro de la perspectiva, y esa elección determina qué seis puntos serán los vértices de los triángulos y qué línea será el eje de la perspectiva.
El pequeño teorema de Desargues [ editar ]
Esta versión restringida establece que si dos triángulos son una perspectiva desde un punto en una línea dada, y dos pares de lados correspondientes también se encuentran en esta línea, entonces el tercer par de lados correspondientes también se encuentran en la línea. Por lo tanto, es la especialización del Teorema de Desargues solo en los casos en que el centro de la perspectiva se encuentra en el eje de la perspectiva.
Un plano de Moufang es un plano proyectivo en el que el pequeño teorema de Desargues es válido para cada línea.
En geometría euclidiana , el teorema de la línea de Droz-Farny es una propiedad de dos líneas perpendiculares a través del ortocentro de un triángulo arbitrario.
Dejar ser un triángulo con vértices , y , y deja ser su ortocentro (el punto común de sus tres líneas de altitud . y ser dos líneas rectas perpendiculares entre sí . Dejar, y ser los puntos donde cruza las líneas laterales , y , respectivamente. Del mismo modo, dejemos Let, y ser los puntos donde interseca esas líneas laterales. El teorema de la línea Droz-Farny dice que los puntos medios de los tres segmentos, y son colineales . [1] [2] [3]
El teorema fue declarado por Arnold Droz-Farny en 1899, [1] pero no está claro si tenía una prueba. [4]
La generalización de Goormaghtigh [ editar ]
Una generalización del teorema de la línea Droz-Farny fue probada en 1930 por René Goormaghtigh . [5]
Como arriba, deja ser un triángulo con vértices , y . Dejar ser cualquier punto distinto de , y y ser cualquier línea a través . Dejar, y ser puntos en las líneas laterales , y , respectivamente, de modo que las líneas , y son las imágenes de las líneas , y , respectivamente, por reflexión contra la línea . El teorema de Goormaghtigh luego dice que los puntos, y son colineales
El teorema de la línea Droz-Farny es un caso especial de este resultado, cuando es el ortocentro del triángulo .
La generalización de Dao [ editar ]
Primera generalización: Sea ABC un triángulo, P sea un punto en el plano, deje tres segmentos paralelos AA ', BB', CC 'de modo que sus puntos medios y P sean colineales. Luego, PA ', PB', PC 'se encuentran con BC, CA, AB respectivamente en tres puntos colineales. [6]
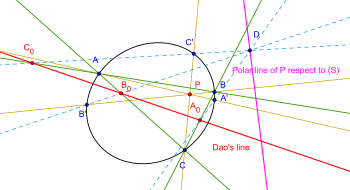
Segunda generalización: Deje una cónica S y un punto P en el plano . Construya tres líneas d a , d b , d c a través de P de manera que se encuentren con la cónica en A, A '; B, B '; C, C 'respectivamente. Sea D un punto en el polar del punto P con respecto a (S) o D se encuentre en la cónica (S). Deje DA '∩ BC = A 0 ; DB '∩ AC = B 0 ; DC '∩ AB = C 0 . Entonces A 0 , B 0 , C 0 son colineales.













































No hay comentarios:
Publicar un comentario