LISTAS DE FORMAS - TRIÁNGULOS

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

6 puntos en los lados del triángulo y su sección cónica común

El teorema de Carnot (llamado así por Lazare Carnot ) describe una relación entre secciones cónicas y triángulos .

En un triangulo $${\ displaystyle ABC} con puntos $${\ displaystyle C_ {A}, C_ {B}} en el lado $${\ displaystyle AB}, $${\ displaystyle A_ {B}, A_ {C}} en el lado $${\ displaystyle BC} y $${\ displaystyle B_ {C}, B_ {A}} en el lado $${\ displaystyle AC} esos seis puntos están ubicados en una sección cónica común si y solo si se cumple la siguiente ecuación:

$${\ displaystyle {\ frac {| AC_ {A} |} {| BC_ {A} |}} \ cdot {\ frac {| AC_ {B} |} {| BC_ {B} |}} \ cdot {\ frac {| BA_ {B} |} {| CA_ {B} |}} \ cdot {\ frac {| BA_ {C} |} {| CA_ {C} |}} \ cdot {\ frac {| CB_ {C} |} {| AB_ {C} |}} \ cdot {\ frac {| CB_ {A} |} {| AB_ {A} |}} = 1}.

el teorema de Carnot establece que la suma de las distancias con signo del circuncentro D a los lados de un triángulo arbitrario ABC es

$${\ displaystyle DF + DG + DH = R + r, \}

donde r es el inradius y R es el circumradius del triángulo. Aquí se considera que el signo de las distancias es negativo si y solo si el segmento de línea abierta DX ( X = F , G , H ) se encuentra completamente fuera del triángulo. En el diagrama, DF es negativo y tanto DG como DH son positivos.

El teorema lleva el nombre de Lazare Carnot (1753-1823). Se utiliza en una prueba del teorema japonés para polígonos concíclicos .

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Teorema de Carnot para perpendiculares en los lados del triángulo:
área azul = área roja

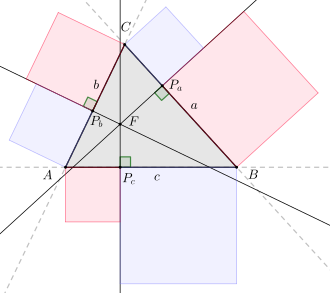
El teorema de Carnot (llamado así por Lazare Carnot ) describe una condición necesaria y suficiente para que un punto común de intersección de tres líneas sea perpendicular a los lados (extendidos) del triángulo. El teorema también puede considerarse como una generalización del teorema de Pitágoras.

Teorema [ editar ]

Para un triangulo $${\ displaystyle \ triangle ABC} con lados $${\ displaystyle a, b, c} considere tres líneas, que son perpendiculares a los lados del triángulo e intersecan en un punto común $${\ displaystyle F}. Si $${\ displaystyle P_ {a}, P_ {b}, P_ {c}} son los puntos de pedal de esos tres perpendiculares en los lados $${\ displaystyle a, b, c}, entonces se cumple la siguiente ecuación:

$${\ displaystyle | AP_ {c} | ^ {2} + | BP_ {a} | ^ {2} + | CP_ {b} | ^ {2} = | BP_ {c} | ^ {2} + | CP_ { a} | ^ {2} + | AP_ {b} | ^ {2}}

Lo contrario de la declaración anterior también es cierto, es decir, si la ecuación se cumple para los puntos de pedal de tres perpendiculares en los tres lados del triángulo, entonces se cruzan en un punto común. Por lo tanto, la ecuación proporciona una condición necesaria y suficiente.

Casos especiales [ editar ]

Si el triangulo $${\ displaystyle \ triangle ABC} tiene un ángulo recto en $${\ displaystyle C} y el punto de intersección $${\ displaystyle F} se encuentra en cualquiera $${\ displaystyle A} o $${\ displaystyle B}, entonces la ecuación anterior produce el teorema de Pitágoras. Por ejemplo si$${\ displaystyle F} coincide con $${\ displaystyle A} entonces esto produce $${\ displaystyle | AP_ {b} | = 0}, $${\ displaystyle | AP_ {c} | = 0}, $${\ displaystyle | CP_ {a} | = 0}, $${\ displaystyle | CP_ {b} | = b}, $${\ displaystyle | BP_ {a} | = a} y $${\ displaystyle | BP_ {c} | = c}. Por lo tanto, la ecuación anterior se transforma en el teorema de Pitágoras.$${\ displaystyle a ^ {2} + b ^ {2} = c ^ {2}}.

Otro corolario es la propiedad de las bisectrices perpendiculares de un triángulo que se cruzan en un punto común. En el caso de las bisectrices perpendiculares tiene$${\ displaystyle | AP_ {c} | = | BP_ {c} |}, $${\ displaystyle | BP_ {a} | = | CP_ {a} |} y $${\ displaystyle | CP_ {b} | = | AP_ {b} |}y por lo tanto, la ecuación anterior es válida. lo que significa que las tres bisectrices perpendiculares se cruzan en el mismo punto.

 centroide o centro geométrico de una figura plana es la posición media aritmética de todos los puntos de la figura. Informalmente, es el punto en el que un corte de la forma podría equilibrarse perfectamente en la punta de un alfiler. ^[1]

La definición se extiende a cualquier objeto en el espacio n - dimensional : su centroide es la posición media de todos los puntos en todas las direcciones de coordenadas. ^[2]

Mientras que en geometría la palabra baricentro es sinónimo de centroide , en astrofísica y astronomía , el baricentro es el centro de masa de dos o más cuerpos que orbitan entre sí. En física , el centro de masa es la media aritmética de todos los puntos ponderados por la densidad local o el peso específico . Si un objeto físico tiene una densidad uniforme, su centro de masa es el mismo que el centroide de su forma.

En geografía , el centroide de una proyección radial de una región de la superficie de la Tierra al nivel del mar es el centro geográfico de la región .

Centroide de un triángulo

Historia [ editar ]

El término "centroide" es de acuñación reciente (1814). Se utiliza como sustituto de los términos más antiguos " centro de gravedad " y " centro de masa ", cuando se deben enfatizar los aspectos puramente geométricos de ese punto. El término es peculiar del idioma inglés. Los franceses usan "centre de gravité" en la mayoría de las ocasiones, y otros usan términos de significado similar.

El centro de gravedad, como su nombre lo indica, es una noción que surgió en la mecánica, muy probablemente en relación con las actividades de construcción. No se sabe cuándo, dónde y quién lo inventó, ya que es un concepto que probablemente ocurrió a muchas personas individualmente con diferencias menores.

Si bien es posible que Euclides todavía estuviera activo en Alejandría durante la infancia de Arquímedes (287-212 a. C.), es cierto que cuando Arquímedes visitó Alejandría , Euclides ya no estaba allí. Por lo tanto, Arquímedes no podría haber aprendido el teorema de que las medianas de un triángulo se encuentran en un punto: el centro de gravedad del triángulo directamente de Euclides, ya que esta proposición no está en los Elementos de Euclides . La primera declaración explícita de esta proposición se debe a la Garza de Alejandría (quizás el siglo I d. C.) y aparece en su Mecánica. Se puede agregar, de paso, que la proposición no se hizo común en los libros de texto sobre geometría plana hasta el siglo XIX.

Si bien Arquímedes no declara esa proposición explícitamente, hace referencias indirectas a ella, sugiriendo que estaba familiarizado con ella. Sin embargo, Jean Etienne Montucla (1725-1799), autor de la primera historia de las matemáticas (1758), declara categóricamente (vol. I, p. 463) que el centro de gravedad de los sólidos es un tema que Arquímedes no tocó.

En 1802 Charles Bossut (1730-1813) publicó un Essai aur PhisMire generale des Mathiques de dos volúmenes. Este libro fue muy apreciado por sus contemporáneos, a juzgar por el hecho de que dos años después de su publicación ya estaba disponible en traducción en italiano (1802–03), inglés (1803) y alemán (1804). Bossut le da crédito a Arquímedes por haber encontrado el centroide de las figuras planas, pero no tiene nada que decir sobre los sólidos. ^[3]

Propiedades [ editar ]

El centroide geométrico de un objeto convexo siempre se encuentra en el objeto. Un objeto no convexo podría tener un centroide que está fuera de la figura misma. El centroide de un anillo o un tazón , por ejemplo, se encuentra en el vacío central del objeto.

Si se define el centroide, es un punto fijo de todas las isometrías en su grupo de simetría . En particular, el centroide geométrico de un objeto se encuentra en la intersección de todos sus hiperplanos de simetría . El centroide de muchas figuras ( polígono regular , poliedro regular , cilindro , rectángulo , rombo , círculo , esfera , elipse , elipsoide , superellipse , superellipsoide , etc.) puede determinarse solo por este principio.

En particular, el centroide de un paralelogramo es el punto de encuentro de sus dos diagonales . Esto no es cierto para otros cuadriláteros .

Por la misma razón, el centroide de un objeto con simetría traslacional no está definido (o se encuentra fuera del espacio cerrado), porque una traducción no tiene un punto fijo.

Ejemplos [ editar ]

El centroide de un triángulo es la intersección de las tres medianas del triángulo (cada mediana conecta un vértice con el punto medio del lado opuesto). ^[4]

Para otras propiedades del centroide de un triángulo, ver abajo .

Localización [ editar ]

Método de línea de plomada [ editar ]

El centroide de una lámina plana uniformemente densa , como en la figura (a) a continuación, puede determinarse experimentalmente utilizando una plomaday un alfiler para encontrar el centro de masa colocado de un cuerpo delgado de densidad uniforme que tiene la misma forma. El pasador sujeta el cuerpo, insertado en un punto, fuera del supuesto centroide de tal manera que pueda girar libremente alrededor del pasador; la línea de plomada se deja caer desde el pasador (figura b). La posición de la plomada se traza en la superficie, y el procedimiento se repite con el pasador insertado en cualquier punto diferente (o varios puntos) fuera del centroide del objeto. El único punto de intersección de estas líneas será el centroide (figura c). Siempre que el cuerpo tenga una densidad uniforme, todas las líneas hechas de esta manera incluirán el centroide, y todas las líneas se cruzarán exactamente en el mismo lugar.

(una)	(si)	(C)

Este método puede extenderse (en teoría) a formas cóncavas donde el centroide puede estar fuera de la forma, y ​​prácticamente a sólidos (de nuevo, de densidad uniforme), donde el centroide puede estar dentro del cuerpo. Las posiciones (virtuales) de las líneas de plomada deben registrarse por otros medios que no sean dibujándolos a lo largo de la forma.

Método de equilibrio [ editar ]

Para formas bidimensionales convexas, el centroide se puede encontrar equilibrando la forma en una forma más pequeña, como la parte superior de un cilindro estrecho. El centroide ocurre en algún lugar dentro del rango de contacto entre las dos formas (y exactamente en el punto donde la forma se equilibraría en un alfiler). En principio, se pueden usar cilindros progresivamente más estrechos para encontrar el centroide con precisión arbitraria. En la práctica, las corrientes de aire hacen que esto no sea factible. Sin embargo, al marcar el rango de superposición de múltiples balanzas, se puede lograr un nivel considerable de precisión.

De un conjunto finito de puntos [ editar ]

El centroide de un conjunto finito de $${\ displaystyle {k}} puntos $${\ displaystyle \ mathbf {x} _ {1}, \ mathbf {x} _ {2}, \ ldots, \ mathbf {x} _ {k}} en $${\ displaystyle \ mathbb {R} ^ {n}} es

$${\ displaystyle \ mathbf {C} = {\ frac {\ mathbf {x} _ {1} + \ mathbf {x} _ {2} + \ cdots + \ mathbf {x} _ {k}} {k}} }. ^[2]

Este punto minimiza la suma de las distancias al cuadrado euclidianas entre sí y cada punto del conjunto.

Por descomposición geométrica [ editar ]

El centroide de una figura plana $${\ displaystyle X} se puede calcular dividiéndolo en un número finito de figuras más simples $${\ displaystyle X_ {1}, X_ {2}, \ dots, X_ {n}}, computando el centroide $${\ displaystyle C_ {i}} y área $${\ displaystyle A_ {i}} de cada parte, y luego computación

$${\ displaystyle C_ {x} = {\ frac {\ sum C_ {i_ {x}} A_ {i}} {\ sum A_ {i}}}, C_ {y} = {\ frac {\ sum C_ {i_ {y}} A_ {i}} {\ sum A_ {i}}}}

Agujeros en la figura $${\ displaystyle X}, las superposiciones entre las partes o las partes que se extienden fuera de la figura se pueden manejar usando áreas negativas $${\ displaystyle A_ {i}}. A saber, las medidas$${\ displaystyle A_ {i}} debe tomarse con signos positivos y negativos de tal manera que la suma de los signos de $${\ displaystyle A_ {i}} para todas las partes que encierran un punto dado $${\ displaystyle p} es 1 si $${\ displaystyle p} pertenece a $${\ displaystyle X}, y 0 de lo contrario.

Por ejemplo, la figura a continuación (a) se divide fácilmente en un cuadrado y un triángulo, ambos con área positiva; y un agujero circular, con área negativa (b).

(a) Objeto 2D

(b) Objeto descrito usando elementos más simples

(c) Centroides de elementos del objeto

El centroide de cada parte se puede encontrar en cualquier lista de centroides de formas simples (c). Entonces el centroide de la figura es el promedio ponderado de los tres puntos. La posición horizontal del centroide, desde el borde izquierdo de la figura es

$${\ displaystyle x = {\ frac {5 \ times 10 ^ {2} +13.33 \ times {\ frac {1} {2}} 10 ^ {2} -3 \ times \ pi 2.5 ^ {2}} {10 ^ {2} + {\ frac {1} {2}} 10 ^ {2} - \ pi 2.5 ^ {2}}} \ aproximadamente 8.5 {\ mbox {unidades}}.}

La posición vertical del centroide se encuentra de la misma manera.

La misma fórmula es válida para cualquier objeto tridimensional, excepto que cada $${\ displaystyle A_ {i}} debe ser el volumen de $${\ displaystyle X_ {i}}, en lugar de su área. También es válido para cualquier subconjunto de$${\ displaystyle \ mathbb {R} ^ {d}}, para cualquier dimensión $${\ displaystyle d}, con las áreas reemplazadas por $${\ displaystyle d}dimensionales medidas de las piezas.

Por fórmula integral [ editar ]

El centroide de un subconjunto X de $${\ displaystyle \ mathbb {R} ^ {n}}también puede ser calculado por la integral

$${\ displaystyle C = {\ frac {\ int xg (x) \; dx} {\ int g (x) \; dx}}}

donde las integrales se toman en todo el espacio $${\ displaystyle \ mathbb {R} ^ {n}}, yg es la función característica del subconjunto, que es 1 dentro de X y 0 fuera de él. ^[5] Obsérvese que el denominador es simplemente la medida del conjunto X . Esta fórmula no se puede aplicar si el conjunto X tiene una medida cero, o si cualquiera de las integrales diverge.

Otra fórmula para el centroide es

$${\ displaystyle C_ {k} = {\ frac {\ int zS_ {k} (z) \; dz} {\ int S_ {k} (z) \; dz}}}

donde C _k es la coordenada k de C , y S _k ( z ) es la medida de la intersección de X con el hiperplano definido por la ecuación x _k = z . Una vez más, el denominador es simplemente la medida de X .

Para una figura plana, en particular, las coordenadas del baricentro son

$${\ displaystyle C _ {\ mathrm {x}} = {\ frac {\ int xS _ {\ mathrm {y}} (x) \; dx} {A}}}

$${\ displaystyle C _ {\ mathrm {y}} = {\ frac {\ int yS _ {\ mathrm {x}} (y) \; dy} {A}}}

donde A es el área de la figura X ; S _y ( x ) es la longitud de la intersección de X con la línea vertical en abscisa x ; y S _x ( y ) es la cantidad análoga para los ejes intercambiados.

Región limitada [ editar ]

El centroide $${\ displaystyle ({\ bar {x}}, \; {\ bar {y}})}de una región limitada por las gráficas de las funciones continuas $${\ displaystyle f} y $${\ displaystyle g} tal que $${\ displaystyle f (x) \ geq g (x)} en el intervalo $${\ displaystyle [a, b]}, $${\ displaystyle a \ leq x \ leq b}, es dado por

$${\ displaystyle {\ bar {x}} = {\ frac {1} {A}} \ int _ {a} ^ {b} x [f (x) -g (x)] \; dx}^[5]

$${\ displaystyle {\ bar {y}} = {\ frac {1} {A}} \ int _ {a} ^ {b} \ left [{\ frac {f (x) + g (x)} {2 }} \ right] [f (x) -g (x)] \; dx,}^[6]

dónde $${\ displaystyle A} es el área de la región (dada por $${\ displaystyle \ int _ {a} ^ {b} [f (x) -g (x)] \; dx}) ^[7] [8]

De un objeto en forma de L [ editar ]

Este es un método para determinar el centroide de un objeto en forma de L.

1. Divida la forma en dos rectángulos, como se muestra en la figura 2. Encuentre los centroides de estos dos rectángulos dibujando las diagonales. Dibuja una línea que une los centroides. El centroide de la forma debe estar en esta línea AB.
2. Divida la forma en otros dos rectángulos, como se muestra en la figura 3. Encuentre los centroides de estos dos rectángulos dibujando las diagonales. Dibuja una línea que une los centroides. El centroide de la forma de L debe estar en esta línea CD.
3. Como el centroide de la forma debe estar a lo largo de AB y también a lo largo de CD, debe estar en la intersección de estas dos líneas, en O. El punto O puede estar dentro o fuera del objeto en forma de L.

De un triángulo [ editar ]

El centroide de un triángulo es el punto de intersección de sus medianas (las líneas que unen cada vértice con el punto medio del lado opuesto). ^[4] El centroide divide cada una de las medianas en la proporción 2: 1, lo que quiere decir que se encuentra ⅓ de la distancia de cada lado al vértice opuesto (ver figuras a la derecha). ^[9] [10] Sus coordenadas cartesianas son las medias de las coordenadas de los tres vértices. Es decir, si los tres vértices son$${\ displaystyle L = (x_ {L}, y_ {L}),} $${\ displaystyle M = (x_ {M}, y_ {M}),} y $${\ displaystyle N = (x_ {N}, y_ {N}),}entonces el centroide (denotado C aquí pero más comúnmente denotado G en la geometría del triángulo ) es

$${\ displaystyle C = {\ frac {1} {3}} (L + M + N) = \ left ({\ frac {1} {3}} (x_ {L} + x_ {M} + x_ {N }), \; \; {\ frac {1} {3}} (y_ {L} + y_ {M} + y_ {N}) \ right).}

El centroide está por lo tanto en $${\ displaystyle {\ tfrac {1} {3}}: {\ tfrac {1} {3}}: {\ tfrac {1} {3}}}en coordenadas barcéntricas .

En coordenadas trilineales, el centroide puede expresarse en cualquiera de estas formas equivalentes en términos de las longitudes laterales a, b, c y ángulos de vértice L, M, N : ^[11]

${\displaystyle {\begin{aligned}C&={\frac {1}{a}}:{\frac {1}{b}}:{\frac {1}{c}}=bc:ca:ab=\csc L:\csc M:\csc N\\[6pt]&=\cos L+\cos M\cdot \cos N:\cos M+\cos N\cdot \cos L:\cos N+\cos L\cdot \cos M\\[6pt]&=\sec L+\sec M\cdot \sec N:\sec M+\sec N\cdot \sec L:\sec N+\sec L\cdot \sec M.\end{aligned}}}$

El centroide también es el centro físico de masa si el triángulo está hecho de una lámina de material uniforme; o si toda la masa se concentra en los tres vértices, y se divide equitativamente entre ellos. Por otro lado, si la masa se distribuye a lo largo del perímetro del triángulo, con una densidad lineal uniforme , entonces el centro de masa se encuentra en el centro de Spieker (el incentro del triángulo medial ), que no coincide (en general) con el geométrico. centroide del triángulo completo.

El área del triángulo es 1.5 veces la longitud de cualquier lado multiplicado por la distancia perpendicular del lado al centroide. ^[12]

El centroide de un triángulo se encuentra en su línea de Euler entre su ortocentro H y su circuncentro O , exactamente dos veces más cerca del último que del primero:

$${\ displaystyle {\ overline {CH}} = 2 {\ overline {CO}}.}^[13] [14]

Además, para el incentro I y el centro N de nueve puntos , tenemos

{\ displaystyle {\ begin {alineado} {\ overline {CH}} & = 4 {\ overline {CN}} \\ [5pt] {\ overline {CO}} & = 2 {\ overline {CN}} \\ [5pt] {\ overline {IC}} & <{\ overline {HC}} \\ [5pt] {\ overline {IH}} y <{\ overline {HC}} \\ [5pt] {\ overline {IC }} & <{\ overline {IO}} \ end {alineado}}}

Si G es el centroide del triángulo ABC, entonces:

$${\ displaystyle \ displaystyle ({\ text {Area of}} \ triangle \ mathrm {ABG}) = ({\ text {Area of}} \ triangle \ mathrm {ACG}) = ({\ text {Area of}} \ triangle \ mathrm {BCG}) = {\ frac {1} {3}} ({\ text {Área de}} \ triangle \ mathrm {ABC})}

El conjugado isogonal del centroide de un triángulo es su punto simétrico .

Cualquiera de las tres medianas a través del centroide divide el área del triángulo por la mitad. Esto no es cierto para otras líneas a través del centroide; la mayor desviación de la división de áreas iguales ocurre cuando una línea a través del centroide es paralela a un lado del triángulo, creando un triángulo más pequeño y un trapezoide ; en este caso, el área del trapecio es 5/9 del triángulo original. ^[15]

Deje que P sea cualquier punto en el plano de un triángulo con vértices A, B, y C y centroide G . Entonces, la suma de las distancias al cuadrado de P desde los tres vértices excede la suma de las distancias al cuadrado del centroide G desde los vértices en tres veces la distancia al cuadrado entre P y G :

$${\ displaystyle PA ^ {2} + PB ^ {2} + PC ^ {2} = GA ^ {2} + GB ^ {2} + GC ^ {2} + 3PG ^ {2}.}^[dieciséis]

La suma de los cuadrados de los lados del triángulo es igual a tres veces la suma de las distancias al cuadrado del centroide desde los vértices:

$${\ displaystyle AB ^ {2} + BC ^ {2} + CA ^ {2} = 3 (GA ^ {2} + GB ^ {2} + GC ^ {2}).}^[dieciséis]

El centroide de un triángulo es el punto que maximiza el producto de las distancias dirigidas de un punto desde las líneas laterales del triángulo. ^[17]

Sea ABC un triángulo, sea G su centroide y D , E y F sean los puntos medios de BC , CA y AB , respectivamente. Para cualquier punto P en el plano de ABC entonces

$${\ displaystyle PA + PB + PC \ leq 2 (PD + PE + PF) + 3PG.}^[18]

De un polígono [ editar ]

El centroide de un polígono cerrado sin intersección propia definido por n vértices ( x ₀ , y ₀ ), ( x ₁ , y ₁ ), ..., ( x _n −1 , y _n −1 ) es el punto ( C _x , C _y ), ^[19] donde

$${\ displaystyle C _ {\ mathrm {x}} = {\ frac {1} {6A}} \ sum _ {i = 0} ^ {n-1} (x_ {i} + x_ {i + 1}) ( x_ {i} \ y_ {i + 1} -x_ {i + 1} \ y_ {i})} y

$${\ displaystyle C _ {\ mathrm {y}} = {\ frac {1} {6A}} \ sum _ {i = 0} ^ {n-1} (y_ {i} + y_ {i + 1}) ( x_ {i} \ y_ {i + 1} -x_ {i + 1} \ y_ {i})} ,

y donde A es el área firmada del polígono, ^[19] como se describe en la fórmula del cordón :

$${\ displaystyle A = {\ frac {1} {2}} \ sum _ {i = 0} ^ {n-1} (x_ {i} \ y_ {i + 1} -x_ {i + 1} \ y_ {yo}).}

En estas fórmulas, se supone que los vértices están numerados en orden de ocurrencia a lo largo del perímetro del polígono; además, se supone que el vértice ( x _n , y _n ) es el mismo que ( x ₀ , y ₀ ), lo que significa$${\ displaystyle i + 1} en el último caso debe girar para $${\ displaystyle i = 0}. ^{[ cita requerida ]} (Si los puntos están numerados en el sentido de las agujas del reloj, el área A , calculada como arriba, será negativa; sin embargo, las coordenadas del centroide serán correctas incluso en este caso. ^{[ cita requerida ]} )

De un cono o pirámide [ editar ]

El centroide de un cono o pirámide se encuentra en el segmento de línea que conecta el vértice con el centroide de la base. Para un cono sólido o pirámide, el centroide es 1/4 de la distancia desde la base hasta el vértice. Para un cono o pirámide que es solo un caparazón (hueco) sin base, el centroide es 1/3 de la distancia desde el plano base hasta el ápice.

De un tetraedro y una simplex n- dimensional [ editar ]

Un tetraedro es un objeto en el espacio tridimensional que tiene cuatro triángulos como caras . Un segmento de línea que une un vértice de un tetraedro con el centroide de la cara opuesta se llama mediana , y un segmento de línea que une los puntos medios de dos bordes opuestos se llama bimediano . Por lo tanto, hay cuatro medianas y tres bimedianos. Estos siete segmentos de línea se encuentran en el centroide del tetraedro. ^[20] Las medianas se dividen por el centroide en la proporción 3: 1. El centroide de un tetraedro es el punto medio entre su punto Monge y el circuncentro (centro de la esfera circunscrita). Estos tres puntos definen elLínea de Euler del tetraedro que es análoga a la línea de un triángulo de Euler .

Estos resultados se generalizan a cualquier simplex n- dimensional de la siguiente manera. Si el conjunto de vértices de un simplex es$${\ displaystyle {v_ {0}, \ ldots, v_ {n}}}, considerando los vértices como vectores , el centroide es

$${\ displaystyle C = {\ frac {1} {n + 1}} \ sum _ {i = 0} ^ {n} v_ {i}.}

El centroide geométrico coincide con el centro de masa si la masa se distribuye uniformemente sobre todo el simplex, o se concentra en los vértices como n masas iguales.

De un hemisferio [ editar ]

El centroide de un hemisferio sólido (es decir, la mitad de una bola sólida) divide el segmento de línea que conecta el centro de la esfera con el polo del hemisferio en la proporción 3: 8. El centroide de un hemisferio hueco (es decir, la mitad de una esfera hueca) divide el segmento de línea que conecta el centro de la esfera con el polo del hemisferio por la mitad.