LISTAS DE FORMAS - TRIÁNGULOS

De Wikipedia, la enciclopedia libre

  (Redirigido desde el teorema del triángulo isósceles )

Saltar a navegaciónSaltar a búsqueda

Los pons asinorum en la edición de Byrne de los Elementos que muestran parte de la prueba de Euclides.

En geometría , la afirmación de que los ángulos opuestos a los lados iguales de un triángulo isósceles son ellos mismos iguales es conocido como los pons Asinorum ( latín:  [pos asɪnoːrũː] , Inglés: / p ɒ n z ˌ æ s ɪ n ɔr ə m / PONZ ass-i- NOR -əm ), generalmente traducido como "puente de asnos ". Esta declaración es la Propuesta 5 del Libro 1 de Euclides 's Elementos , y también se conoce como elTeorema del triángulo isósceles . Lo contrario también es cierto: si dos ángulos de un triángulo son iguales, entonces los lados opuestos a ellos también son iguales. El término también se aplica al teorema de Pitágoras. ^[1] .

El nombre de esta declaración también se usa metafóricamente para un problema o desafío que separará la certeza de lo simple, el pensador de la flota de lo lento, lo determinado de lo más atrevido, para representar una prueba crítica de habilidad o comprensión. El primer uso conocido es 1645.

Pruebas [ editar ]

Prueba de Proclus

Elementos de Euclides Libro 1, proposición 5; los pons asinorum

Euclides y Proclus [ editar ]

La declaración de Euclides de los pons asinorum incluye una segunda conclusión de que si los lados iguales del triángulo se extienden por debajo de la base, entonces los ángulos entre las extensiones y la base también son iguales. La prueba de Euclides implica dibujar líneas auxiliares a estas extensiones. Pero, como señala el comentarista de Euclides, Proclus , Euclides nunca usa la segunda conclusión y su prueba puede simplificarse un poco dibujando las líneas auxiliares a los lados del triángulo, el resto de la prueba procede de la misma manera.

Ha habido mucha especulación y debate sobre por qué Euclides agregó la segunda conclusión al teorema, dado que hace que la prueba sea más complicada. Una explicación plausible, dada por Proclus, es que la segunda conclusión puede usarse en posibles objeciones a las pruebas de proposiciones posteriores en las que Euclides no cubre todos los casos. ^[3] La prueba se basa en gran medida en lo que hoy se llama lado-ángulo-lado , la proposición anterior en los Elementos .

La variación de Proclus de la prueba de Euclides procede de la siguiente manera: ^[4]
Sea ABC un triángulo isósceles con AB y AC como lados iguales. Elija un punto arbitrario D en el lado AB y construya E en AC para que AD = AE. Dibuja las líneas BE, DC y DE.
Considere los triángulos BAE y CAD; BA = CA, AE = AD, y$${\ displaystyle \ angle A}es igual a sí mismo, por lo que, por el lado del ángulo, los triángulos son congruentes y los lados y ángulos correspondientes son iguales.
Por lo tanto$${\ displaystyle \ angle ABE = \ angle ACD} y $${\ displaystyle \ angle ADC = \ angle AEB}y BE = CD.
Como AB = AC y AD = AE, BD = CE por sustracción de partes iguales.
Ahora considere los triángulos DBE y ECD; BD = CE, BE = CD y$${\ displaystyle \ angle DBE = \ angle ECD}acaban de mostrarse, por lo que aplicando nuevamente lado-ángulo-lado, los triángulos son congruentes.
Por lo tanto, el ángulo BDE = ángulo CED y el ángulo BED = ángulo CDE.
Dado que el ángulo BDE = ángulo CED y el ángulo CDE = ángulo BED, el ángulo BDC = ángulo CEB por sustracción de partes iguales.
Considere un tercer par de triángulos, BDC y CEB; DB = EC, DC = EB, y ángulo BDC = ángulo CEB, entonces aplicando lado-ángulo-lado por tercera vez, los triángulos son congruentes.
En particular, el ángulo CBD = BCE, que debía ser probado.

Pappus [ editar ]

Proclus da una prueba mucho más corta atribuida a Pappus de Alejandría . Esto no solo es más simple, sino que no requiere ninguna construcción adicional. El método de prueba es aplicar lado-ángulo-lado al triángulo y su imagen especular. Los autores más modernos, imitando el método de prueba dado para la proposición anterior, han descrito esto como levantar el triángulo, darle la vuelta y colocarlo sobre sí mismo. ^[5] Charles Lutwidge Dodgson evoca este método en Euclides y sus modernos rivales , calificándolo de " toro irlandés " porque aparentemente requiere que el triángulo esté en dos lugares a la vez. ^[6]

La prueba es la siguiente: ^[7]
Sea ABC un triángulo isósceles con AB y AC como lados iguales.
Considere los triángulos ABC y ACB, donde ACB se considera un segundo triángulo con vértices A, C y B correspondientes respectivamente a A, B y C en el triángulo original.
$${\ displaystyle \ angle A}es igual a sí mismo, AB = AC y AC = AB, por lo que, por el lado del ángulo, los triángulos ABC y ACB son congruentes.
En particular,$${\ displaystyle \ angle B = \ angle C}. ^[8]

Otros [ editar ]

Una prueba de libro de texto

Un método de libro de texto estándar es construir la bisectriz del ángulo en A. ^[9] Esto es más simple que la prueba de Euclides, pero Euclides no presenta la construcción de una bisectriz angular hasta la proposición 9. Por lo tanto, el orden de presentación de las proposiciones de Euclides sería deben cambiarse para evitar la posibilidad de razonamiento circular.

La prueba procede de la siguiente manera: ^[10]
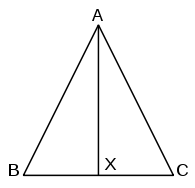
Como antes, dejemos que el triángulo sea ABC con AB = AC.
Construya la bisectriz angular de$${\ displaystyle \ angle BAC}y extiéndalo para encontrar BC en X.
AB = AC y AX es igual a sí mismo.
Además,$${\ displaystyle \ angle BAX = \ angle CAX}, entonces, aplicando lado-ángulo-lado, el triángulo BAX y el triángulo CAX son congruentes.
Se deduce que los ángulos en B y C son iguales.

Legendre usa una construcción similar en Éléments de géométrie , pero tomando X como el punto medio de BC. ^[11] La prueba es similar, pero de lado lado lado debe ser utilizado en lugar de en el lado lateral de ángulo, y de lado lado lado no se da por Euclides hasta más tarde en el Elementos .

En espacios interiores de productos [ editar ]

El teorema del triángulo isósceles se mantiene en espacios internos de productos sobre los números reales o complejos . En tales espacios, toma una forma que dice de los vectores x , y y z que si ^[12]

$${\ displaystyle x + y + z = 0 {\ text {and}} \ | x \ | = \ | y \ |,}

entonces

$${\ displaystyle \ | xz \ | = \ | yz \ |.}

Ya que

$${\ displaystyle \ | xz \ | ^ {2} = \ | x \ | ^ {2} -2x \ cdot z + \ | z \ | ^ {2},}

y

$${\ displaystyle x \ cdot z = \ | x \ | \ | z \ | \ cos \ theta}

donde θ es el ángulo entre los dos vectores, la conclusión de esta forma espacial interna del producto del teorema es equivalente a la afirmación sobre la igualdad de ángulos.

Etimología y términos relacionados [ editar ]

Otro término medieval para los pons asinorum fue Elefuga , que, según Roger Bacon , proviene de la elegía griega "miseria" y del latín fuga "vuelo", es decir "vuelo de los desgraciados". Aunque esta etimología es dudosa, se hace eco en el uso de Chaucer del término "flemyng of wreches" para el teorema. ^[13]

Hay dos posibles explicaciones para el nombre pons asinorum , la más simple es que el diagrama utilizado se asemeja a un puente real. Pero la explicación más popular es que es la primera prueba real en los Elementos de la inteligencia del lector y funciona como un "puente" a las proposiciones más difíciles que siguen. ^[14] Gauss supuestamente una vez adoptó una creencia similar en la necesidad de comprender de inmediato la identidad de Euler como punto de referencia para convertirse en un matemático de primera clase. ^[15]

Del mismo modo, el nombre de Dulcarnon se le dio a la 47ª proposición del Libro I de Euclides, más conocido como el teorema de Pitágoras , después del árabe Dhū 'l qarnain ذُو ٱلْقَرْنَيْن, que significa "el dueño de los dos cuernos", porque los diagramas del teorema mostraban dos cuadrados más pequeños como cuernos en la parte superior de la figura. El término también se usa como metáfora de un dilema. ^[13] El teorema también a veces se llamaba "el molino de viento" por razones similares. ^[dieciséis]

Uso metafórico [ editar ]

Los usos de los pons asinorum como metáfora incluyen:

• Philobiblon de Richard Aungerville contiene el pasaje "Quot Euclidis discipulos retrojecit Elefuga cuasi scopulos eminens et abruptus, qui nullo scalarum suffragio scandi posset! Durus, consulta, ¿es su sermo; quis potest eum audire?", Que compara el teorema con un acantilado escarpado que ninguna escalera puede ayudar a escalar y pregunta cuántos posibles geómetras han sido rechazados. ^[13]
• El término pons asinorum , tanto en su significado como puente y como prueba, se utiliza como metáfora para encontrar el término medio de un silogismo . ^[13]
• El poeta del siglo XVIII Thomas Campbell escribió un poema humorístico llamado "Pons asinorum" donde una clase de geometría ataca el teorema mientras una compañía de soldados podría cargar una fortaleza; la batalla no estuvo exenta de bajas. ^[17]
• El economista John Stuart Mill llamó a la Ley de la Renta de Ricardo los pons como ininorum de la economía. ^[18]
• Pons Asinorum es el nombre dado a una configuración particular ^[19] de un cubo de Rubik .
• Eric Raymond se refirió al tema del espacio en blanco sintácticamente significativo en el lenguaje de programación Python como su pons asinorum. ^[20]
• La aasinsilta finlandesa y la åsnebrygga sueca es una técnica literaria en la que una conexión tenue, incluso artificial, entre dos argumentos o temas, que es casi, pero no del todo inadvertida , se utiliza como una transición incómoda entre ellos. ^[21] En texto serio, se considera un error estilístico, ya que pertenece adecuadamente a la corriente de la conciencia , o causalidad. estilo escrito. Los ejemplos típicos son terminar una sección diciendo de qué se trata la siguiente sección, sin molestarse en explicar por qué los temas están relacionados, expandir una mención casual en un tratamiento detallado o encontrar una conexión artificial entre los temas (por ejemplo, "Compramos vino tinto ; hablando de líquidos rojos, mañana es el Día Mundial del Donante de Sangre ").
• En holandés , ezelsbruggetje ('pequeño puente de asnos') es la palabra para un mnemotécnico . Lo mismo es cierto para el alemán Eselsbrücke .
• En checo , oslí můstek tiene dos significados: puede describir una conexión artificial entre dos temas o un mnemotécnico.

conjugado isotómico de un punto P con respecto a un triángulo ABC es otro punto, definido de manera específica a partir de P y ABC : si los puntos base de las líneas PA , PB y PC en los lados opuestos a A, B , y C se refleja sobre los puntos medios de sus respectivos lados, las líneas resultantes se cortan en el congugate isotónico de P .

Construcción [ editar ]

Suponemos que P no es colineal con dos vértices de ABC . Sean A ', B ' y C 'los puntos en los que las líneas AP , BP , CP se encuentran con las líneas laterales BC , CA y AB ( extendidas si es necesario). Reflejando A ', B ', C 'en los puntos medios de los lados BC , CA , AB dará los puntos A ", B " y C "respectivamente.líneas isotónico AA ", BB 'y CC ' unirse a estos nuevos puntos a los vértices se encuentran en un punto (que se puede probar usando el teorema de Ceva ), el conjugado isotónico de P .

Coordenadas [ editar ]

Si los trilineales para P son p  : q  : r , entonces los trilineales para el conjugado isotómico de P son

a ⁻² p ⁻¹  : b ⁻² q ⁻¹  : c ⁻² r ⁻¹ ,

donde a, b y c son las longitudes de los lados opuestos vértices A, B, y C , respectivamente.

Propiedades [ editar ]

El conjugado isotómico del centroide del triángulo ABC es el centroide mismo.

El conjugado isotómico del punto symmedian es el tercer punto de Brocard , y el conjugado isotómico del punto de Gergonne es el punto de Nagel .

Los conjugados isotómicos de líneas son circuncónicos y, por el contrario, los conjugados isotómicos de circunconos son líneas. (Esta propiedad también es válida para los conjugados isogonales ).

conjugado isotómico de un punto P con respecto a un triángulo ABC es otro punto, definido de manera específica a partir de P y ABC : si los puntos base de las líneas PA , PB y PC en los lados opuestos a A, B , y C se refleja sobre los puntos medios de sus respectivos lados, las líneas resultantes se cortan en el congugate isotónico de P .

Construcción [ editar ]

Suponemos que P no es colineal con dos vértices de ABC . Sean A ', B ' y C 'los puntos en los que las líneas AP , BP , CP se encuentran con las líneas laterales BC , CA y AB ( extendidas si es necesario). Reflejando A ', B ', C 'en los puntos medios de los lados BC , CA , AB dará los puntos A ", B " y C "respectivamente.líneas isotónico AA ", BB 'y CC ' unirse a estos nuevos puntos a los vértices se encuentran en un punto (que se puede probar usando el teorema de Ceva ), el conjugado isotónico de P .

Coordenadas [ editar ]

Si los trilineales para P son p  : q  : r , entonces los trilineales para el conjugado isotómico de P son

a ⁻² p ⁻¹  : b ⁻² q ⁻¹  : c ⁻² r ⁻¹ ,

donde a, b y c son las longitudes de los lados opuestos vértices A, B, y C , respectivamente.

Propiedades [ editar ]

El conjugado isotómico del centroide del triángulo ABC es el centroide mismo.

El conjugado isotómico del punto symmedian es el tercer punto de Brocard , y el conjugado isotómico del punto de Gergonne es el punto de Nagel .

Los conjugados isotómicos de líneas son circuncónicos y, por el contrario, los conjugados isotómicos de circunconos son líneas. (Esta propiedad también es válida para los conjugados isogonales ).