LISTAS DE FORMAS - TRIÁNGULOS

De Wikipedia, la enciclopedia libre

  (Redirigido desde el punto de Jacobi )

Saltar a navegaciónSaltar a búsqueda

Los ángulos de colores adyacentes son iguales en medida. El punto N es el punto de Jacobi para el triángulo ABC y estos ángulos.

En geometría plana , un punto de Jacobi es un punto en el plano euclídeo determinado por un triángulo ABC y un triple de ángulos α , β y γ . Esta información es suficiente para determinar tres puntos X , Y y Z de manera que ∠ ZAB = ∠ YAC = α , ∠ XBC = ∠ ZBA = β y ∠ YCA = ∠ XCB = γ . Luego, por un teorema de Karl Friedrich Andreas Jacobi [ de ] , las líneas AX, BY y CZ son concurrentes , ^{[1] [2] [3]} en un punto N llamado el punto de Jacobi. ^[3]

El punto de Jacobi es una generalización del punto de Fermat , que se obtiene dejando α = β = γ = 60 ° y un triángulo ABC que no tiene ángulo mayor o igual a 120 °.

Si los tres ángulos anteriores son iguales, entonces N se encuentra en la hipérbola rectangular dada en coordenadas de área por

$${\ displaystyle yz (\ cot B- \ cot C) + zx (\ cot C- \ cot A) + xy (\ cot A- \ cot B) = 0,}

que es la hipérbola de Kiepert . Cada elección de tres ángulos iguales determina un centro triangular .

De Wikipedia, la enciclopedia libre

  (Redirigido del teorema japonés para polígonos concíclicos )

Saltar a navegaciónSaltar a búsqueda

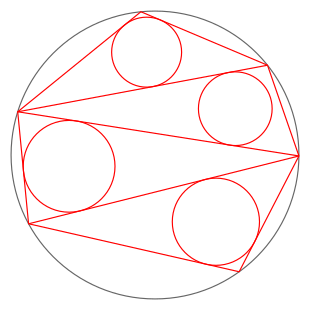
En geometría , el teorema japonés establece que no importa cómo se triangule un polígono cíclico , la suma de inradii de triángulos es constante . ^{[1] : pág. 193}

suma de los radios de los círculos verdes = suma de los radios de los círculos rojos

Por el contrario, si la suma de inradii es independiente de la triangulación, entonces el polígono es cíclico. El teorema japonés se desprende del teorema de Carnot ; Es un problema de Sangaku .

Prueba [ editar ]

Este teorema se puede probar probando primero un caso especial: no importa cómo se triangule un cuadrilátero cíclico , la suma de inradios de triángulos es constante.

Después de probar el caso cuadrilátero, el caso general del teorema del polígono cíclico es un corolario inmediato. La regla del cuadrilátero se puede aplicar a los componentes del cuadrilátero de una partición general de un polígono cíclico, y la aplicación repetida de la regla, que "voltea" una diagonal, generará todas las particiones posibles de cualquier partición dada, con cada "volteo" preservando el suma de los inradii.

El caso del cuadrilátero se deduce de una extensión simple del teorema japonés para los cuadriláteros cíclicos , que muestra que un rectángulo está formado por los dos pares de centros que corresponden a las dos posibles triangulaciones del cuadrilátero. Los pasos de este teorema no requieren nada más allá de la geometría euclidiana constructiva básica. ^[2]

Con la construcción adicional de un paralelogramo que tiene lados paralelos a las diagonales y tangentes a las esquinas del rectángulo de los centros, el caso cuadrilátero del teorema del polígono cíclico se puede probar en unos pocos pasos. La igualdad de las sumas de los radios de los dos pares es equivalente a la condición de que el paralelogramo construido sea un rombo, y esto se muestra fácilmente en la construcción.

Otra prueba del caso cuadrilátero está disponible debido a Wilfred Reyes (2002). ^[3] En la prueba, tanto el teorema japonés para los cuadriláteros cíclicos como el caso cuadrilátero del teorema del polígono cíclico se prueban como consecuencia del problema III de Thébault .

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

El teorema de Johnson establece que si los tres círculos azules de la imagen tienen el mismo radio e intersectan en un solo punto, H , entonces el círculo rojo resultante tiene el mismo radio que los círculos azules. El triángulo verde ΔJ _A J _B J _C es entonces el triángulo Johnson del triángulo de referencia negro, ΔABC, y tiene un círculo circunferencial (naranja) de radio r .

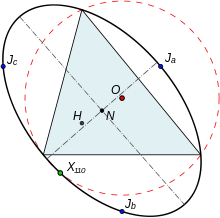
En geometría , un conjunto de círculos Johnson comprende tres círculos de igual radio r compartiendo un punto de intersección común H . En tal configuración, los círculos generalmente tienen un total de cuatro intersecciones (puntos donde al menos dos de ellas se encuentran): el punto común H que comparten, y para cada uno de los tres pares de círculos, un punto de intersección más (denominado aquí su intersección en dos sentidos). Si dos de los círculos se osculan, solo tienen H como punto común, y luego se considerará que Hser su intersección de 2 sabios también; si deben coincidir declaramos su intersección 2-sabia sea el punto opuesto diametralmente H . Los tres puntos de intersección de 2 sentidos definen el triángulo de referencia de la figura. El concepto lleva el nombre de Roger Arthur Johnson.

Propiedades [ editar ]

El círculo anticomplementario (rojo, radio 2 r ) de ΔABC es tangente a los tres círculos de Johnson, que tienen centros en las líneas (naranja) entre la intersección común, H y los puntos de tangencia. Estos puntos de tangencia forman el triángulo anticomplementario , ΔP _A P _B P _C , verde.

1. Los centros de los círculos Johnson se encuentran en un círculo del mismo radio r como los círculos Johnson centradas en H . Estos centros forman el triángulo de Johnson .
2. El círculo centrado en H con radio 2 r , conocido como círculo anticomplementario, es tangente a cada uno de los círculos de Johnson. Los tres puntos tangentes son reflejos del punto H sobre los vértices del triángulo Johnson.
3. Los puntos de tangencia entre los círculos de Johnson y el círculo anticomplementario forman otro triángulo, llamado triángulo anticomplementario del triángulo de referencia. Es similar al triángulo de Johnson, y es homotético por un factor 2 centrado en H , su circuncentro común.
4. Teorema de Johnson : los puntos de intersección en dos sentidos de los círculos de Johnson (vértices del triángulo de referencia ABC ) se encuentran en un círculo del mismo radio r que los círculos de Johnson. Esta propiedad también es conocida en Rumania como el problema de las monedas de 5 lei de Gheoghe Ţiţeica .
5. El triángulo de referencia es de hecho congruente con el triángulo de Johnson, y es homotético a él por un factor −1.
6. El punto H es el ortocentro del triángulo de referencia y el circuncentro del triángulo de Johnson.
7. El centro homotético del triángulo de Johnson y el triángulo de referencia es su centro común de nueve puntos .

Pruebas [ editar ]

La propiedad 1 es obvia a partir de la definición. La propiedad 2 también es clara: para cualquier círculo de radio r , y cualquier punto P en él, el círculo de radio 2 r centrado en P es tangente al círculo en su punto opuesto a P ; esto se aplica en particular a P = H , dando el círculo anticomplementaria C . La propiedad 3 en la formulación de la homotecia sigue inmediatamente; El triángulo de puntos de tangencia se conoce como el triángulo anticomplementario.

Para las propiedades 4 y 5, primero observe que dos de los tres círculos de Johnson están intercambiados por la reflexión en la línea que conecta H y su intersección en dos sentidos (o en su tangente común en H si estos puntos deben coincidir), y esta reflexión También intercambia los dos vértices del triángulo anticomplementario que se encuentra en estos círculos. Por lo tanto, el punto de intersección de 2 sentidos es el punto medio de un lado del triángulo anticomplementario, y H se encuentra en la bisectriz perpendicularde este lado Ahora los puntos medios de los lados de cualquier triángulo son las imágenes de sus vértices por una homotecia con factor ½, centrada en el baricentro del triángulo. Aplicado al triángulo anticomplementario, que a su vez se obtiene del triángulo de Johnson por una homotetería con factor 2, se deduce de la composición de las homotedades que el triángulo de referencia es homotético al triángulo de Johnson por un factor −1. Como tal homotecia es una congruencia , esto le da la propiedad 5, y también el teorema de los círculos de Johnson, ya que los triángulos congruentes tienen círculos circunscritos de igual radio.

Para la propiedad 6, ya se estableció que las bisectrices perpendiculares de los lados del triángulo anticomplementario pasan todas por el punto H ; Como ese lado es paralelo a un lado del triángulo de referencia, estas bisectrices perpendiculares también son las altitudes del triángulo de referencia.

La propiedad 7 se deduce inmediatamente de la propiedad 6, ya que el centro homotetico cuyo factor es -1 debe estar en el punto medio de los circuncentros  O del triángulo de referencia y  H del triángulo de Johnson; este último es el ortocentro del triángulo de referencia, y se sabe que su centro de nueve puntos es ese punto medio. Dado que la simetría central también asigna el ortocentro del triángulo de referencia al del triángulo de Johnson, el centro homotético también es el centro de nueve puntos del triángulo de Johnson.

También hay una prueba algebraica del teorema de los círculos de Johnson, utilizando un simple cálculo vectorial. Hay vectores$${\ displaystyle {\ vec {u}}}, $${\ displaystyle {\ vec {v}}}y $${\ displaystyle {\ vec {w}}}, todos de longitud r , de modo que los círculos de Johnson estén centrados respectivamente en$${\ displaystyle H + {\ vec {u}}}, $${\ displaystyle H + {\ vec {v}}}y $${\ displaystyle H + {\ vec {w}}}. Entonces los puntos de intersección de 2 sentidos son respectivamente$${\ displaystyle H + {\ vec {u}} + {\ vec {v}}}, $${\ displaystyle H + {\ vec {u}} + {\ vec {w}}}y $${\ displaystyle H + {\ vec {v}} + {\ vec {w}}}y el punto $${\ displaystyle H + {\ vec {u}} + {\ vec {v}} + {\ vec {w}}}claramente tiene una distancia r a cualquiera de esos puntos de intersección de 2 sentidos.

Más propiedades [ editar ]

Los tres círculos de Johnson pueden considerarse los reflejos del círculo del triángulo de referencia sobre cada uno de los tres lados del triángulo de referencia. Además, bajo las reflexiones sobre los tres lados del triángulo de referencia, su ortocentro H se asigna a tres puntos en la circunferencia del triángulo de referencia que forman los vértices del triángulo circuntérico , su circuncentro O se asigna a los vértices del triángulo Johnson y su línea Euler (línea que pasa por O , N y H ) genera tres líneas que son concurrentes en X (110).

Johnson circunconico

El triángulo de Johnson y su triángulo de referencia comparten el mismo centro de nueve puntos, la misma línea de Euler y el mismo círculo de nueve puntos . Los seis puntos formados a partir de los vértices del triángulo de referencia y su triángulo Johnson se encuentran en la circuncónica de Johnson que está centrada en el centro de nueve puntos y que tiene el punto X (216) del triángulo de referencia como su perspector. La circuncónica y la circunferencia comparten un cuarto punto, X (110) del triángulo de referencia.

Finalmente, hay dos circuncúbicos interesantes y documentados que pasan por los seis vértices del triángulo de referencia y su triángulo Johnson, así como el circuncentro, el ortocentro y el centro de nueve puntos. El primero se conoce como el primer cúbico de Musselman - K 026. Este cúbico también pasa a través de los seis vértices del triángulo medial y el triángulo medial del triángulo de Johnson. El segundo cúbico se conoce como el cúbico central de Euler - K 044. Este cúbico también pasa a través de los seis vértices del triángulo órtico y el triángulo órtico del triángulo Johnson.

La notación de punto X ( i ) es la clasificación ETC de Clark Kimberling de los centros de triángulo.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Un triángulo de Kepler es un triángulo rectángulo formado por tres cuadrados con áreas en progresión geométrica de acuerdo con la proporción áurea .

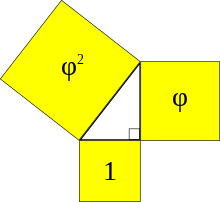
Un triángulo de Kepler es un triángulo rectángulo con longitudes de borde en una progresión geométrica en la cual la razón común es √ φ , donde φ es la razón dorada , ^[a] y se puede escribir:$${\ displaystyle 1: {\ sqrt {\ varphi}}: \ varphi}, o aproximadamente 1: 1.272: 1.618 . ^[1] Los cuadrados de los bordes de este triángulo están en progresión geométrica de acuerdo con la proporción áurea.

Los triángulos con tales proporciones llevan el nombre del matemático y astrónomo alemán Johannes Kepler (1571-1630), quien demostró por primera vez que este triángulo se caracteriza por una proporción entre su lado corto y la hipotenusa igual a la proporción dorada. ^{[2] Los} triángulos de Kepler combinan dos conceptos matemáticos clave, el teorema de Pitágoras y la proporción áurea, que fascinaron profundamente a Kepler, ya que expresó:

La geometría tiene dos grandes tesoros: uno es el teorema de Pitágoras, el otro la división de una línea en razón extrema y media. Lo primero que podemos comparar con una masa de oro, lo segundo lo podemos llamar una joya preciosa. ^[3]

Algunas fuentes afirman que un triángulo con dimensiones que se aproximan mucho a un triángulo de Kepler puede reconocerse en la Gran Pirámide de Giza , ^[4] [5] convirtiéndolo en una pirámide dorada .

Derivación [ editar ]

El hecho de que un triángulo con bordes $${\ displaystyle 1}, $${\ displaystyle {\ sqrt {\ varphi}}} y $${\ displaystyle \ varphi}, forma un triángulo rectángulo que se sigue directamente de la reescritura del polinomio cuadrático definitorio para la proporción áurea $${\ displaystyle \ varphi}:

$${\ displaystyle \ varphi ^ {2} = \ varphi +1}

en la forma del teorema de Pitágoras :

$${\ displaystyle (\ varphi) ^ {2} = ({\ sqrt {\ varphi}}) ^ {2} + (1) ^ {2}.}

Relación con la media aritmética, geométrica y armónica [ editar ]

Para los números reales positivos a y b , su media aritmética , media geométrica y media armónica son las longitudes de los lados de un triángulo rectángulo si y solo si ese triángulo es un triángulo de Kepler. ^[6]

Construyendo un triángulo Kepler [ editar ]

Un método para construir un triángulo Kepler a través de un rectángulo dorado

Se puede construir un triángulo Kepler con solo regla y brújula creando primero un rectángulo dorado :

1. Construir un cuadrado unitario
2. Dibuja una línea desde el punto medio de un lado del cuadrado hasta una esquina opuesta
3. Use esa línea como radio para dibujar un arco que defina la altura del rectángulo
4. Completa el rectángulo dorado
5. Use el lado más largo del rectángulo dorado para dibujar un arco que interseque el lado opuesto del rectángulo y defina la hipotenusa del triángulo de Kepler.

Kepler lo construyó de manera diferente. En una carta a su antiguo profesor Michael Mästlin , escribió: "Si en una línea que se divide en relación extrema y media, se construye un triángulo rectángulo, de modo que el ángulo recto esté en la posición perpendicular en el punto de sección, entonces el la pierna más pequeña será igual al segmento más grande de la línea dividida ". ^[2]

Una coincidencia matemática [ editar ]

El círculo y el cuadrado tienen aproximadamente el mismo perímetro.

En el triángulo de Kepler con lados $${\ displaystyle 1, {\ sqrt {\ varphi}}, \ varphi,} considerar:

• el círculo que lo circunscribe, y
• un cuadrado con el lado igual al borde mediano del triángulo.

Entonces los perímetros del cuadrado ($${\ displaystyle 4 {\ sqrt {\ varphi}}}) y el círculo ($${\ displaystyle \ pi \ varphi}) coinciden hasta un error inferior al 0.1%.

Esta es la coincidencia matemática $${\ displaystyle \ pi \ approx 4 / {\ sqrt {\ varphi}}}. El cuadrado y el círculo no pueden tener exactamente el mismo perímetro, porque en ese caso uno podría resolver el problema clásico (imposible) de la cuadratura del círculo . En otras palabras,$${\ displaystyle \ pi \ neq 4 / {\ sqrt {\ varphi}}} porque $${\ displaystyle \ pi}es un número trascendental .

Según algunas fuentes, los triángulos Kepler aparecen en el diseño de las pirámides egipcias. La diagonal del piso de la Cámara del Rey , más el ancho de la cámara, dividida por la longitud de la cámara, está muy cerca de la proporción dorada. ^[5] [7] Sin embargo, según varios estudiosos que han investigado esta relación, los antiguos egipcios probablemente no sabían la coincidencia matemática que implicaba el número$${\ displaystyle \ pi} y la proporción áurea $${\ displaystyle \ varphi}.