LISTAS DE FORMAS - TRIÁNGULOS

El problema del triángulo de Kobon es un problema no resuelto en geometría combinatoria planteada por primera vez por Kobon Fujimura . El problema requiere el mayor número N ( k ) de triángulos no superpuestos cuyos lados se encuentran en una disposición de k líneas . Las variaciones del problema consideran el plano proyectivo en lugar del plano euclidiano, y requieren que los triángulos no sean cruzados por ninguna otra línea de la disposición. ^[1]

Saburo Tamura demostró que el número entero más grande que no excede k ( k  - 2) / 3 proporciona un límite superior en el número máximo de triángulos no superpuestos realizables por k líneas. ^[2] En 2007, Johannes Bader y Gilles Clément encontraron un límite superior más estricto, al demostrar que no se podía alcanzar el límite superior de Tamura para ninguna k congruente con 0 o 2 (mod 6). ^[3] El número máximo de triángulos es, como máximo, uno menos que el límite de Tamura en estos casos. Se conocen soluciones perfectas (soluciones de triángulos de Kobon que producen el número máximo de triángulos) para k = 3, 4, 5, 6, 7, 8, 9, 13, 15 y 17. ^[4] Para k = 10, 11 y 12, las mejores soluciones conocidas alcanzan varios triángulos uno menos que el límite superior.

Como lo demostraron G. Clément y J. Bader, ^[3] las soluciones para k > 2 están limitadas anteriormente por

$${\ displaystyle k (k-2) / 3}, cuando k == {3, 5} (mod 6);

$${\ displaystyle (k + 1) (k-3) / 3}, cuando k == {0, 2} (mod 6);

$${\ displaystyle (k ^ {2} -2k-2) / 3}, cuando k == {1, 4} (mod 6).

(La función de piso se maneja observando que la expresión k ( k  - 2) es un múltiplo de 3 en el primer caso y 2 más que un múltiplo de 3 en el tercer caso; Clément y Bader solo mejoraron el límite en el caso del medio .)

Dada una solución perfecta con k ₀ > 3 líneas, se pueden encontrar otros números de solución de triángulo de Kobon para todos los valores k _i donde

$${\ displaystyle k_ {n + 1} = 2 \ cdot k_ {n} -1,}

utilizando el procedimiento de D. Forge y JL Ramirez Alfonsin. ^[1] [5] Por ejemplo, la solución para k ₀ = 5 conduce al número máximo de triángulos no superpuestos para k = 5,9,17,33,65, ...

k	3	4 4	5 5	6 6	7 7	8	9 9	10	11	12	13	14	15	dieciséis	17	18 años	19	20	21	OEIS
Límite superior de Tamura en N ( k )	1	2	5 5	8	11	dieciséis	21	26	33	40	47	56	sesenta y cinco	74	85	96	107	120	133	A032765
Clément y el límite superior de Bader	1	2	5 5	7 7	11	15	21	26	33	39	47	55	sesenta y cinco	74	85	95	107	119	133	-
solución mejor conocida	1	2	5 5	7 7	11	15	21	25	32	38	47	53	sesenta y cinco	72	85	93	104	115	130

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

X (54) es el punto de Kosnita del triángulo ABC

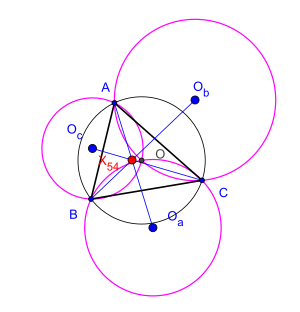
En geometría euclidiana , el teorema de Kosnita es una propiedad de ciertos círculos asociados con un triángulo arbitrario .

Dejar $${\ displaystyle ABC} ser un triángulo arbitrario $${\ displaystyle O}su circuncentro y$${\ displaystyle O_ {a}, O_ {b}, O_ {c}} son los circuncentros de tres triángulos $${\ displaystyle OBC}, $${\ displaystyle OCA}y $${\ displaystyle OAB}respectivamente. El teorema afirma que las tres líneas rectas $${\ displaystyle AO_ {a}}, $${\ displaystyle BO_ {b}}y $${\ displaystyle CO_ {c}}son concurrentes ^[1] Este resultado fue establecido por el matemático rumano Cezar Coşniţă (1910-1962). ^[2]

Su punto de concurrencia se conoce como el punto Kosnita del triángulo (nombrado por Rigby en 1997). Es el conjugado isogonal del centro de nueve puntos . ^[3] [4] Es el centro del triángulo $${\ displaystyle X (54)}en la lista de Clark Kimberling . ^[5] Este teorema es un caso especial del teorema de Dao en seis circuncentros asociados con un hexágono cíclico en.

Este artículo trata sobre el significado geométrico. Para la planta, ver Phyllanthus .

Un triángulo rectángulo donde c ₁ y c ₂ son los catetos yh es la hipotenusa

En un triángulo rectángulo , un cateto (originalmente de la palabra griega Κάθετος ; plural: catheti ), comúnmente conocido como pata , es cualquiera de los lados adyacentes al ángulo recto . Ocasionalmente se llama un "lado sobre el ángulo recto". El lado opuesto al ángulo recto es la hipotenusa . En el contexto de la hipotenusa, los catheti a veces se denominan simplemente "los otros dos lados".

Si los catetos de un triángulo rectángulo tienen la misma longitud, el triángulo es isósceles . Si tienen diferentes longitudes, se puede hacer una distinción entre el cateto menor (más corto) y el mayor (más largo). La razón de las longitudes de los catheti define las funciones trigonométricas tangentes y cotangentes de los ángulos agudos en el triángulo: la razón$${\ displaystyle c_ {1} / c_ {2}} es la tangente del ángulo agudo adyacente a $${\ displaystyle c_ {2}} y también es la cotangente del ángulo agudo adyacente a $${\ displaystyle c_ {1}}.

En un triángulo rectángulo, la longitud de un cathetus es la media geométrica de la longitud del segmento adyacente cortado por la altitud a la hipotenusa y la longitud de toda la hipotenusa.

Según el teorema de Pitágoras , la suma de los cuadrados de las longitudes de los catheti es igual al cuadrado de la longitud de la hipotenusa.

El término pata , además de referirse a un cateto de un triángulo rectángulo, también se usa para referirse a cualquiera de los lados iguales de un triángulo isósceles o a cualquiera de los lados no paralelos de un trapecio .

el problema de Lemoine es un cierto problema de construcción en geometría de plano elemental planteado por el matemático francés Émile Lemoine (1840-1912) en 1868. ^[1] [2] El problema se publicó como la Pregunta 864 en Nouvelles Annales de Mathématiques (Serie 2 , Volumen 7 (1868), p 191). El principal interés en el problema es que una discusión sobre la solución del problema por Ludwig Kiepert publicada en Nouvelles Annales de Mathématiques (serie 2, Volumen 8 (1869), págs. 40–42) contenía una descripción de una hipérbola. que ahora se conoce como la hipérbola de Kiepert.

Declaración del problema [ editar ]

La pregunta publicada por Lemoine plantea el siguiente problema de construcción:

Dado un vértice de cada uno de los triángulos equiláteros colocados a los lados de un triángulo , construye el triángulo original.

La solución de Ludwig Kiepert [ editar ]

Diagrama que ilustra el Lema 1.

Diagrama que ilustra la solución de Ludwig Kiepert al problema de Lemoine

Kiepert establece la validez de su construcción demostrando algunos lemas . ^[3] [4]

Problema

Sean A ₁ , B ₁ , C ₁ los vértices de los triángulos equiláteros ubicados a los lados de un triángulo ABC . Dada A ₁ , B ₁ , C ₁ constructo A , B , C .

Lema 1

Si en los tres lados de un triángulo arbitrario ABC , uno describe triángulos equiláteros ABC ₁ , ACB ₁ , BCA ₁ , entonces los segmentos de línea AA ₁ , BB ₁ , C C ₁ son iguales, coinciden en un punto P y los ángulos se forman entre sí son iguales a 60 °.

Lema 2

Si en A ₁ B ₁ C ₁ se hace la misma construcción que en ABC , habrá tres triángulos equiláteros A ₁ B ₁ C ₂ , A ₁ C ₁ B ₂ , B ₁ C ₁ A ₂ , tres segmentos de línea iguales A ₁ a ₂ , B ₁ B ₂ , C ₁ C ₂ , que también concurrir en el punto P .

Lema 3

A , B , C son respectivamente los puntos medios de A ₁ A ₂ , B ₁ B ₂ , C ₁ C ₂ .

Solución

• Describa en los segmentos A ₁ B ₁ , A ₁ C ₁ , B ₁ C ₁ los triángulos equiláteros A ₁ B ₁ C ₂ , A ₁ C ₁ B ₂ , B ₁ C ₁ A ₂ , respectivamente.
• Los puntos medios de A ₁ A ₂ , B ₁ B ₂ , C ₁ C ₂ son, respectivamente, los vértices A , B , C del triángulo requerido.

Otras soluciones [ editar ]

Varias otras personas además de Kiepert presentaron sus soluciones durante 1868–9, incluidos los Sres. Williere (en Arlon), Brocard, Claverie (Lycee de Clermont), Joffre (Lycee Charlemagne), Racine (Lycee de Poitiers), Augier (Lycee de Caen ), V. Niebylowski y L. Henri Lorrez. La solución de Kiepert fue más completa que las demás.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Los puntos de Fermat $${\ displaystyle X_ {13}, X_ {14}}, el centro $${\ displaystyle X_ {5}} del círculo de nueve puntos (azul claro) y el circuncentro $${\ displaystyle X_ {3}} del triángulo verde se encuentran en el círculo de Lester (negro).

En plano euclidiano geometría , teorema de Lester estados que en cualquier triángulo escaleno , los dos puntos de Fermat , el centro de nueve puntos , y el circuncentro se encuentran en el mismo círculo . El resultado lleva el nombre de June Lester, quien lo publicó en 1997, ^[1] y el círculo a través de estos puntos fue llamado el círculo de Lester por Clark Kimberling . ^[2] Lester demostró el resultado utilizando las propiedades de números complejos ; autores posteriores han presentado pruebas elementales ^{[3] [4] [5] [6]}, pruebas usando aritmética vectorial, ^[7] y pruebas computarizadas.