LISTAS DE FORMAS - TRIÁNGULOS

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Los puntos isodinámicos. $${\ displaystyle S} y $${\ displaystyle S '}como puntos de intersección comunes de los círculos de Apolonio . Las líneas azules y rojas son las bisectrices de los ángulos interiores y exteriores, que se utilizan para construir los círculos.

En la geometría euclidiana , los puntos isodinámicos de un triángulo son puntos asociados con el triángulo, con las propiedades de que una inversión centrada en uno de estos puntos transforma el triángulo dado en un triángulo equilátero , y que las distancias desde el punto isodinámico hasta los vértices del triángulo son inversamente proporcionales a las longitudes de los lados opuestos del triángulo. Los triángulos que son similares entre sí tienen puntos isodinámicos en las ubicaciones correspondientes en el plano, por lo que los puntos isodinámicos son centros triangulares , y a diferencia de otros centros triangulares, los puntos isodinámicos también son invariantes bajo las transformaciones de Möbius.. Un triángulo que es equilátero tiene un punto isodinámico único, en su centroide ; cada triángulo no equilátero tiene dos puntos isodinámicos. Los puntos isodinámicos fueron estudiados y nombrados por primera vez por Joseph Neuberg  ( 1885 ).

Relaciones de distancia [ editar ]

Los puntos isodinámicos se definieron originalmente a partir de ciertas igualdades de proporciones (o equivalente de productos) de distancias entre pares de puntos. Si$${\ displaystyle S} y $${\ displaystyle S '} son los puntos isodinámicos de un triángulo $${\ displaystyle ABC}, entonces los tres productos de distancias $${\ displaystyle AS \ cdot BC = BS \ cdot AC = CS \ cdot AB}son iguales. Las igualdades análogas también son válidas para$${\ displaystyle S '}. ^[2] Equivalente a la fórmula del producto, las distancias$${\ displaystyle AS}, $${\ displaystyle BS}y $${\ displaystyle CS} son inversamente proporcionales a las longitudes laterales del triángulo correspondientes $${\ displaystyle BC}, $${\ displaystyle AC}y $${\ displaystyle AB}.

$${\ displaystyle S} y $${\ displaystyle S '}son los puntos de intersección comunes de los tres círculos de Apolonio asociados con el triángulo de un triángulo$${\ displaystyle ABC}, los tres círculos que pasan a través de un vértice del triángulo y mantienen una proporción constante de distancias a los otros dos vértices. ^[3] Por lo tanto, línea$${\ displaystyle SS '}es el eje radical común para cada uno de los tres pares de círculos de Apolonio. La bisectriz perpendicular del segmento de línea$${\ displaystyle SS '}es la línea Lemoine , que contiene los tres centros de los círculos de Apolonio. ^[4]

Transformaciones [ editar ]

Los puntos isodinámicos. $${\ displaystyle S} y $${\ displaystyle S '} de un triángulo $${\ displaystyle ABC}También puede definirse por sus propiedades con respecto a las transformaciones del plano, y particularmente con respecto a las inversiones y las transformaciones de Möbius (productos de inversiones múltiples). Inversión del triángulo.$${\ displaystyle ABC}con respecto a un punto isodinámico transforma el triángulo original en un triángulo equilátero . ^[5] Inversión con respecto al círculo del triángulo$${\ displaystyle ABC}deja el triángulo invariante pero transforma un punto isodinámico en el otro. ^[3] Más generalmente, los puntos isodinámicos son equivalentes bajo las transformaciones de Möbius : el par desordenado de puntos isodinámicos de una transformación de$${\ displaystyle ABC} es igual a la misma transformación aplicada al par $${\ displaystyle \ {S, S '\}}. Los puntos isodinámicos individuales se fijan mediante transformaciones de Möbius que mapean el interior del círculo circunferencial de$${\ displaystyle ABC}al interior del círculo circunferencial del triángulo transformado, e intercambiados por transformaciones que intercambian el interior y el exterior del círculo circunferencial. ^[6]

Ángulos [ editar ]

Tres círculos, cada uno formando ángulos de π / 3 con el círculo circunferencial y entre sí, se encuentran en el primer punto isodinámico.

Además de ser las intersecciones de los círculos de Apolonio, cada punto isodinámico es el punto de intersección de otro triple de círculos. El primer punto isodinámico es la intersección de tres círculos a través de los pares de puntos.$${\ displaystyle AB}, $${\ displaystyle AC}y $${\ displaystyle BC}, Donde cada uno de estos círculos se cruza con la circunferencia circunscrita de triángulo$${\ displaystyle ABC}para formar una lente con ángulo de vértice 2π / 3. Del mismo modo, el segundo punto isodinámico es la intersección de tres círculos que se cruzan en el círculo para formar lentes con ángulo de vértice π / 3. ^[6]

Los ángulos formados por el primer punto isodinámico con los vértices del triángulo satisfacen las ecuaciones. $${\ displaystyle ASB = ACB + \ pi / 3}, $${\ displaystyle ASC = ABC + \ pi / 3}y $${\ displaystyle BSC = BAC + \ pi / 3}. Análogamente, los ángulos formados por el segundo punto isodinámico satisfacen las ecuaciones.$${\ displaystyle AS'B = ACB- \ pi / 3}, $${\ displaystyle AS'C = ABC- \ pi / 3}y $${\ displaystyle BS'C = BAC- \ pi / 3}. ^[6]

El triángulo del pedal de un punto isodinámico, el triángulo formado al soltar perpendiculares de$${\ displaystyle S} a cada uno de los tres lados del triángulo $${\ displaystyle ABC}, es equilátero, ^[5] como es el triángulo formado al reflejar$${\ displaystyle S}a través de cada lado del triángulo. ^[7] Entre todos los triángulos equiláteros inscritos en triángulo$${\ displaystyle ABC}, el triángulo del pedal del primer punto isodinámico es el que tiene un área mínima. ^[8]

Propiedades adicionales [ editar ]

Los puntos isodinámicos son los conjugados isogonales de los dos puntos de triángulo de Fermat.$${\ displaystyle ABC}, y viceversa. ^[9]

El cúbico de Neuberg contiene los dos puntos isodinámicos. ^[4]

Si un círculo se divide en tres arcos, el primer punto isodinámico de los puntos finales del arco es el único punto dentro del círculo con la propiedad de que cada uno de los tres arcos es igualmente probable que sea el primer arco alcanzado por un movimiento browniano que comienza en ese punto . Es decir, el punto isodinámico es el punto para el cual la medida armónica de los tres arcos es igual. ^[10]

Construcción [ editar ]

Construcción del punto isodinámico a partir de copias reflejadas del triángulo dado y triángulos equiláteros que apuntan hacia adentro.

El círculo de Apolonio a través del vértice. $${\ displaystyle A} de triángulo $${\ displaystyle ABC}puede construirse encontrando las dos bisectrices de ángulo (interior y exterior) de los dos ángulos formados por líneas$${\ displaystyle AB} y $${\ displaystyle AC} en el vértice $${\ displaystyle A}e intersectando estas líneas bisectrices con línea $${\ displaystyle BC}. El segmento de línea entre estos dos puntos de intersección es el diámetro del círculo de Apolonio. Los puntos isodinámicos se pueden encontrar construyendo dos de estos círculos y encontrando sus dos puntos de intersección. ^[3]

Otra brújula y construcción recta implica encontrar el reflejo $${\ displaystyle A '} de vértice $${\ displaystyle A} a través de la línea $${\ displaystyle BC} (la intersección de círculos centrados en $${\ displaystyle B} y $${\ displaystyle C} mediante $${\ displaystyle A}), y construyendo un triángulo equilátero hacia adentro en el lado $${\ displaystyle BC} del triángulo (el ápice $${\ displaystyle A ''} de este triángulo es la intersección de dos círculos que tienen $${\ displaystyle BC}como su radio). La línea$${\ displaystyle A'A ''} cruza las líneas construidas de manera similar $${\ displaystyle B'B ''} y $${\ displaystyle C'C ''}en el primer punto isodinámico El segundo punto isodinámico puede construirse de manera similar pero con los triángulos equiláteros erigidos hacia afuera en lugar de hacia adentro. ^[11]

Alternativamente, la posición del primer punto isodinámico se puede calcular a partir de sus coordenadas trilineales , que son ^[12]

$${\ displaystyle \ sin (A + \ pi / 3): \ sin (B + \ pi / 3): \ sin (C + \ pi / 3).}

El segundo punto isodinámico usa coordenadas trilineales con una fórmula similar que involucra $${\ displaystyle - \ pi / 3} en lugar de $${\ displaystyle \ pi / 3}.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Conjugado isogonal de P .

Transformación conjugada isogonal sobre los puntos dentro del triángulo.

En geometría , el conjugado isogonal de un punto P con respecto a un triángulo ABC se construye reflejando las líneas PA , PB y PC alrededor de las bisectrices de los ángulos de A , B y C, respectivamente. Estas tres líneas reflejadas concurren en el conjugado isogonal de P . (Esta definición se aplica solo a los puntos que no están en una línea lateral del triángulo ABC ). Este es un resultado directo de la forma trigonométrica del teorema de Ceva .

El conjugado isogonal de un punto P a veces se denota por P * . El conjugado isogonal de P * es P .

El conjugado isogonal del incentivo I es él mismo. El conjugado isogonal de la orthocentre H es el circuncentro O . El conjugado isogonal del centroide G es (por definición) el punto simediano K . Los conjugados isogonales de los puntos de Fermat son los puntos isodinámicos y viceversa. Los puntos de Brocard son conjugados isogonales entre sí.

En coordenadas trilineales , si X = x  : y  : z es un punto que no está en una línea lateral del triángulo ABC , entonces su conjugado isogonal es 1 / x  : 1 / y  : 1 / z . Por esta razón, el conjugado isogonal de X a veces se denota por X  ⁻¹ . El conjunto S de centros triangulares bajo producto trilineal, definido por

( p  : q  : r ) * ( u  : v  : w ) = pu  : qv  : rw ,

es un grupo conmutativo, y el inverso de cada X en S es X  ⁻¹ .

Como la conjugación isogonal es una función, tiene sentido hablar del conjugado isogonal de conjuntos de puntos, como líneas y círculos. Por ejemplo, el conjugado isogonal de una línea es circunconico ; específicamente, una elipse, una parábola o una hipérbola de acuerdo con la línea que interseca el círculo en 0, 1 o 2 puntos. El conjugado isogonal del círculo es la línea en el infinito. Varios cúbicos bien conocidos (p. Ej., Cúbico de Thompson, cúbico de Darboux, cúbico de Neuberg) son autoconjugados isogonales, en el sentido de que si X está en el cúbico, entonces X  ⁻¹ también está en el cúbico.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

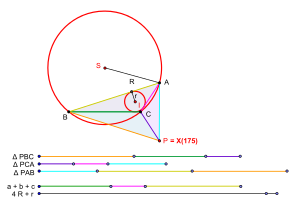
En geometría, el punto isoperimétrico es un punto especial asociado con un triángulo plano . El término fue introducido originalmente por GR Veldkamp en un artículo publicado en el American Mathematical Monthly en 1985 para denotar un punto P en el plano de un triángulo ABC que tiene la propiedad de que los triángulos PBC , PCA y PAB tienen isoperímetros, es decir, propiedad que ^[1] [2]

PB + BC + CP = PC + CA + AP = PA + AB + BP .

Los puntos isoperimétricos en el sentido de Veldkamp existen solo para triángulos que satisfacen ciertas condiciones. El punto isoperimétrico del triángulo ABC en el sentido de Veldkamp, ​​si existe, tiene las siguientes coordenadas trilineales . ^[3]

(sec ( A / 2) cos ( B / 2) cos ( C / 2) - 1, sec ( B / 2) cos ( C / 2) cos ( A / 2) - 1, sec ( C / 2) cos ( A / 2) cos ( B / 2) - 1)

Dado cualquier triángulo ABC, se puede asociar con él un punto P que tiene coordenadas trilineales como se indicó anteriormente. Este punto es un centro triangular y en la Enciclopedia de centros de triángulos (ETC) de Clark Kimberling se llama el punto isoperimétrico del triángulo ABC . Se designa como el centro del triángulo X (175). ^[4] El punto X (175) no necesita ser un punto isoperimétrico del triángulo ABC en el sentido de Veldkamp. Sin embargo, si existe el punto isoperimétrico del triángulo ABC en el sentido de Veldkamp, ​​entonces sería idéntico al punto X (175).

El punto P con la propiedad de que los triángulos PBC , PCA y PAB tienen perímetros iguales se estudió ya en 1890 en un artículo de Emile Lemoine .

Existencia de un punto isoperimétrico en el sentido de Veldkamp [ editar ]

Un triángulo ABC en el que el centro del triángulo X (175) no es el punto isoperimétrico en el sentido de Veldkamp.

Deje que ABC sea ​​cualquier triángulo. Deje que los sidelengths de este triángulo sea una , b , y c . Sea su circunradio R e inradio r . La condición necesaria y suficiente para la existencia de un punto isoperimétrico en el sentido de Veldkamp puede establecerse de la siguiente manera. ^[1]

El triángulo ABC tiene un punto isoperimétrico en el sentido de Veldkamp si y solo si a + b + c > 4 R + r .

Para todos los triángulos angulares agudos ABC tenemos a + b + c > 4 R + r , por lo que todos los triángulos angulares agudos tienen puntos isoperimétricos en el sentido de Veldkamp.

Propiedades [ editar ]

Supongamos que P denota el centro del triángulo X (175) del triángulo ABC . ^[4]

• P se encuentra en la línea que une el incentro y el punto Gergonne del triángulo ABC .
• Los círculos de los triángulos PBC , PCA , PAB son tangentes entre sí en pares. Hay un punto más, a saber, el punto de desvío igual X (176) del triángulo ABC .
• El centro radical de las incircles de los triángulos PBC , PCA , PAB es P . Hay un punto más, a saber, el punto de desvío igual X (176) del triángulo ABC .
• Si P es un punto isoperimétrico del triángulo ABC en el sentido de Veldkamp, ​​entonces los perímetros de los triángulos PBC , PCA , PAB son iguales a 2 Δ / | (4 R + r - ( a + b + c )) | donde Δ es el área, R es el circunradio, r el inradio y a , b , c las longitudes laterales del triángulo ABC . ^[6]

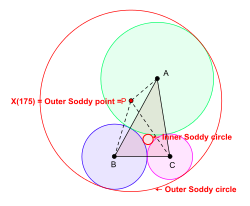
Soddy círculos [ editar ]

Círculos internos y externos de Soddy en el caso en que el punto externo de Soddy es un punto isoperimétrico en el sentido de Veldkamp.

Círculos internos y externos de Soddy en el caso en que el punto externo de Soddy no es un punto isoperimétrico en el sentido de Veldkamp.

Dado un triángulo ABC, se pueden dibujar círculos en el plano del triángulo ABC con centros en A , B y C de manera que sean tangentes entre sí externamente. En general, se pueden dibujar dos círculos nuevos de manera que cada uno de ellos sea tangencial a los tres círculos con A , B , C como centros. (Uno de los círculos puede degenerar en una línea recta). Estos círculos son los círculos Soddy del triángulo ABC . El círculo con el radio más pequeño es el círculo interno de Soddy y su centro se llama punto interno de Soddy o centro interno de Soddy.del triángulo ABC . El círculo con el radio más grande es el círculo externo de Soddy y su centro se llama punto externo de Soddy o centro externo de Soddy del triángulo ABC . ^[6] [7]

El centro del triángulo X (175), el punto isoperimétrico en el sentido de Kimberling, es el punto Soddy externo del triángulo ABC .