LISTAS DE FORMAS - TRIÁNGULOS

desigualdad de Erdős-Mordell establece que para cualquier triángulo ABC y punto P dentro de ABC , la suma de las distancias de P a los lados es menor o igual a la mitad de la suma de las distancias de P a los vértices. Lleva el nombre de Paul Erdős y Louis Mordell . Erdős (1935) planteó el problema de probar la desigualdad; Mordell y DF Barrow ( 1937 ) proporcionaron una prueba dos años después . Sin embargo, esta solución no era muy elemental. Pruebas posteriores más simples fueron encontradas por Kazarinoff (1957) ,Bankoff (1958) y Alsina y Nelsen (2007) .

La desigualdad de Barrow es una versión reforzada de la desigualdad de Erdős-Mordell en la que las distancias de P a los lados se reemplazan por las distancias de P a los puntos donde las bisectrices de ángulo de ∠ APB , ∠ BPC y ∠ CPA cruzan los lados. Aunque las distancias reemplazadas son más largas, su suma aún es menor o igual a la mitad de la suma de las distancias a los vértices.

Declaración [ editar ]

Desigualdad de Erdős-Mordell

Dejar $${\ displaystyle P} ser un punto arbitrario P dentro de un triángulo dado $${\ displaystyle ABC}, y deja $${\ displaystyle PL}, $${\ displaystyle PM}y $${\ displaystyle PN} ser los perpendiculares de $${\ displaystyle P}a los lados de los triángulos. (Si el triángulo es obtuso, uno de estos perpendiculares puede cruzarse a través de un lado diferente del triángulo y terminar en la línea que soporta uno de los lados). Entonces la desigualdad establece que

$${\ displaystyle PA + PB + PC \ geq 2 (PL + PM + PN)}

Prueba [ editar ]

Deje que los lados de ABC ser un opuesto A, b B opuesto, y c opuesto C; también deje que PA = p , PB = q , PC = r , dist (P; BC) = x , dist (P; CA) = y , dist (P; AB) = z . Primero, demostramos que

$${\ displaystyle cr \ geq ax + by.}

Esto es equivalente a

$${\ displaystyle {\ frac {c (r + z)} {2}} \ geq {\ frac {ax + by + cz} {2}}.}

El lado derecho es el área del triángulo ABC, pero en el lado izquierdo, r + z es al menos la altura del triángulo; en consecuencia, el lado izquierdo no puede ser más pequeño que el derecho. Ahora refleje P en la bisectriz de ángulo en C. Encontramos que cr ≥ ay + bx para la reflexión de P. Del mismo modo, bq ≥ az + cx y ap ≥ bz + cy . Resolvemos estas desigualdades para r , q y p :

$${\ displaystyle r \ geq (a / c) y + (b / c) x,}

$${\ displaystyle q \ geq (a / b) z + (c / b) x,}

$${\ displaystyle p \ geq (b / a) z + (c / a) y.}

Sumando los tres, obtenemos

$${\ displaystyle p + q + r \ geq \ left ({\ frac {b} {c}} + {\ frac {c} {b}} \ right) x + \ left ({\ frac {a} {c} } + {\ frac {c} {a}} \ right) y + \ left ({\ frac {a} {b}} + {\ frac {b} {a}} \ right) z.}

Dado que la suma de un número positivo y su recíproco es al menos 2 por la desigualdad AM-GM , hemos terminado. La igualdad es válida solo para el triángulo equilátero, donde P es su centroide.

Otra versión fortalecida [ editar ]

Deje que ABC sea un triángulo inscrito en un círculo (O) y P sea un punto dentro de ABC. Sean D, E, F las proyecciones ortogonales de P sobre BC, CA, AB. M, N, Q son las proyecciones ortogonales de P sobre tangentes a (O) en A, B, C respectivamente, luego:

$${\ displaystyle PM + PN + PQ \ geq 2 (PD + PE + PF)}

La igualdad se cumple si y solo si el triángulo ABC es equilátero ( Dao, Nguyen y Pham 2016 ; Marinescu y Monea 2017 )

Una generalización [ editar ]

Dejar $${\ displaystyle A_ {1} A_ {2} ... A_ {n}} ser un polígono convexo, y $${\ displaystyle P} ser un punto interior de $${\ displaystyle A_ {1} A_ {2} ... A_ {n}}. Dejar$${\ displaystyle R_ {i}} ser la distancia de $${\ displaystyle P} al vértice $${\ displaystyle A_ {i}} , $${\ displaystyle r_ {i}} la distancia desde $${\ displaystyle P} por el lado $${\ displaystyle A_ {i} A_ {i + 1}}, $${\ displaystyle w_ {i}} el segmento de la bisectriz del ángulo $${\ displaystyle A_ {i} PA_ {i + 1}} de $${\ displaystyle P} a su intersección con el lado $${\ displaystyle A_ {i} A_ {i + 1}}entonces ( Lenhard 1961 ):

$${\ displaystyle \ sum _ {i = 1} ^ {n} R_ {i} \ geq \ left (\ sec {\ frac {\ pi} {n}} \ right) \ sum _ {i = 1} ^ { n} w_ {i} \ geq \ left (\ sec {\ frac {\ pi} {n}} \ right) \ sum _ {i = 1} ^ {n} r_ {i}}

 punto de Exeter es un punto especial asociado con un triángulo plano . El punto de Exeter es un centro triangular y se designa como el centro X (22) ^[1] en la Enciclopedia de centros triangulares de Clark Kimberling . Esto se descubrió en un taller de computadoras en matemáticas en la Academia Phillips Exeter en 1986. ^[2] Este es uno de los centros triangulares recientes, que se descubrió solo en 1986, a diferencia de los centros triangulares clásicos como el centroide , el incentro y el punto Steiner. 

Definición [ editar ]

El punto de Exeter se define de la siguiente manera. ^[2] [4]

Deje ABC ser cualquier triángulo dado. Deje que las medianas a través de los vértices A , B , C se encuentren con el círculo del triángulo ABC en A ' , B' y C ' respectivamente. Deje que DEF sea ​​el triángulo formado por las tangentes en A , B y C hasta el círculo del triángulo ABC . (Sea D el vértice opuesto al lado formado por la tangente en el vértice A , E sea ​​el vértice opuesto al lado formado por la tangente en el vérticeB y F son el vértice opuesto al lado formado por la tangente en el vértice C ). Las líneas a través de DA ' , EB' y FC ' son concurrentes . El punto de concurrencia es el punto de Exeter del triángulo ABC .

Coordenadas trilineales [ editar ]

Las coordenadas trilineales del punto de Exeter son

( a ( b ⁴ + c ⁴ - a ⁴ ), b ( c ⁴ + a ⁴ - b ⁴ ), c ( a ⁴ + b ⁴ - c ⁴ )).

Propiedades [ editar ]

• El punto de Exeter del triángulo ABC se encuentra en la línea de Euler (la línea que pasa por el centroide , el ortocentro y el circuncentro ) del triángulo ABC .

teorema del ángulo exterior es la Proposición 1.16 en Elementos de Euclides , que establece que la medida del ángulo exterior de un triángulo es mayor que cualquiera de las medidas de los ángulos interiores remotos. Este es un resultado fundamental en la geometría absoluta porque su prueba no depende del postulado paralelo .

En varios tratamientos de geometría de la escuela secundaria, el término "teorema del ángulo exterior" se ha aplicado a un resultado diferente, ^[1] es decir, la parte de la Proposición 1.32 que establece que la medida del ángulo exterior de un triángulo es igual a la suma de Las medidas de los ángulos interiores remotos. Este resultado, que depende del postulado paralelo de Euclides, se denominará "Teorema del ángulo exterior de la escuela secundaria" (HSEAT) para distinguirlo del teorema del ángulo exterior de Euclides.

Algunos autores se refieren al "Teorema del ángulo exterior de la escuela secundaria" como la forma fuerte del teorema del ángulo exterior y al "Teorema del ángulo exterior de Euclides" como la forma débil .

Ángulos exteriores [ editar ]

Un triángulo tiene tres esquinas, llamadas vértices . Los lados de un triángulo (segmentos de línea) que se unen en un vértice forman dos ángulos (cuatro ángulos si considera que los lados del triángulo son líneas en lugar de segmentos de línea). ^[3] Solo uno de estos ángulos contiene el tercer lado del triángulo en su interior, y este ángulo se llama ángulo interior del triángulo. ^[4] En la imagen a continuación, los ángulos ∠ABC , ∠BCA y ∠CAB son los tres ángulos interiores del triángulo. Un ángulo exteriorse forma al extender uno de los lados del triángulo; El ángulo entre el lado extendido y el otro lado es el ángulo exterior. En la imagen, el ángulo ∠ACD es un ángulo exterior.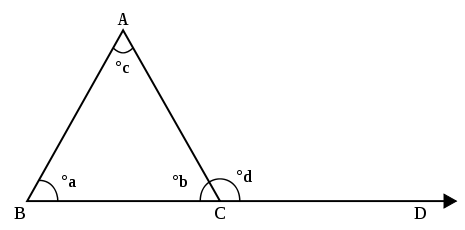

Teorema del ángulo exterior de Euclides [ editar ]

La prueba de la Proposición 1.16 dada por Euclid a menudo se cita como un lugar donde Euclid da una prueba imperfecta. ^{[5] [6] [7]}

Euclides prueba el teorema del ángulo exterior mediante:

• construir el punto medio E del segmento AC,
• dibuja el rayo BE,
• construya el punto F en el rayo BE de modo que E sea (también) el punto medio de B y F,
• dibuja el segmento FC.

Por triángulos congruentes podemos concluir que ∠ BAC = ∠ ECF y ∠ ECF es más pequeño que ∠ ECD, ∠ ECD = ∠ ACD por lo tanto, ∠ BAC es más pequeño que ∠ ACD y lo mismo se puede hacer para el ángulo ∠ CBA dividiendo BC.

La falla radica en el supuesto de que un punto (F, arriba) se encuentra en el ángulo "interno" (∠ ACD). No se da ninguna razón para esta afirmación, pero el diagrama que la acompaña parece una declaración verdadera. Cuando se utiliza un conjunto completo de axiomas para la geometría euclidiana (ver Fundamentos de la geometría ), esta afirmación de Euclides puede probarse. ^[8]

Inválido en geometría esférica [ editar ]

Los triángulos pequeños pueden comportarse de manera casi euclidiana, pero los ángulos exteriores en la base del triángulo grande son 90 °, una contradicción con el teorema del ángulo exterior de Euclides.

El teorema del ángulo exterior no es válido en geometría esférica ni en la geometría elíptica relacionada . Considere un triángulo esférico uno de cuyos vértices es el Polo Norte y los otros dos se encuentran en el ecuador . Los lados del triángulo que emana del Polo Norte ( grandes círculos de la esfera) se encuentran con el ecuador en ángulo recto, por lo que este triángulo tiene un ángulo exterior que es igual a un ángulo interior remoto. El otro ángulo interior (en el Polo Norte) puede hacerse más grande que 90 °, enfatizando aún más el fracaso de esta declaración. Sin embargo, dado que el teorema del ángulo exterior del Euclides es un teorema en geometría absoluta , es automáticamente válido engeometría hiperbólica .

Teorema del ángulo exterior de la escuela secundaria [ editar ]

El teorema del ángulo exterior de la escuela secundaria (HSEAT) dice que el tamaño de un ángulo exterior en un vértice de un triángulo es igual a la suma de los tamaños de los ángulos interiores en los otros dos vértices del triángulo (ángulos interiores remotos). Entonces, en la imagen, el tamaño del ángulo ACD es igual al tamaño del ángulo ABC más el tamaño del ángulo CAB .

El HSEAT es lógicamente equivalente a la declaración euclidiana de que la suma de los ángulos de un triángulo es 180 °. Si se sabe que la suma de las medidas de los ángulos en un triángulo es 180 °, entonces el HSEAT se demuestra de la siguiente manera:

$${\ displaystyle b + d = 180 ^ {\ circ}}

$${\ displaystyle b + d = b + a + c}

$${\ displaystyle \ por lo tanto d = a + c.}

Por otro lado, si el HSEAT se toma como una declaración verdadera, entonces:

$${\ displaystyle d = a + c}

$${\ displaystyle b + d = 180 ^ {\ circ}}

$${\ displaystyle \ por lo tanto b + a + c = 180 ^ {\ circ}.}

Ilustración de la prueba de HSEAT

Demostrando que la suma de las medidas de los ángulos de un triángulo es 180 °.

La prueba euclidiana del HSEAT (y simultáneamente el resultado de la suma de los ángulos de un triángulo) comienza construyendo la línea paralela al lado AB que pasa por el punto C y luego usando las propiedades de los ángulos correspondientes y los ángulos alternos internos de las líneas paralelas a Obtenga la conclusión como en la ilustración. ^[9]

El HSEAT puede ser extremadamente útil cuando se trata de calcular las medidas de ángulos desconocidos en un triángulo.