LISTAS DE FORMAS - TRIÁNGULOS

la desigualdad de Barrow es una desigualdad que relaciona las distancias entre un punto arbitrario dentro de un triángulo , los vértices del triángulo y ciertos puntos en los lados del triángulo.

Sea P un punto arbitrario dentro del triángulo ABC . Desde P y ABC , defina U , V y W como los puntos donde las bisectrices de ángulo de BPC , CPA y APB se cruzan con los lados BC , CA , AB , respectivamente. Entonces la desigualdad de Barrow establece que

$${\ displaystyle PA + PB + PC \ geq 2 (PU + PV + PW), \,}

con igualdad manteniéndose solo en el caso de un triángulo equilátero .

Historia [ editar ]

La desigualdad de Barrow fortalece la desigualdad de Erdős-Mordell , que tiene una forma idéntica, excepto con PU , PV y PW reemplazados por las tres distancias de P desde los lados del triángulo. Lleva el nombre de David Francis Barrow . La prueba de Barrow de esta desigualdad se publicó en 1937, como su solución a un problema planteado en el American Mathematical Monthly de probar la desigualdad de Erdős-Mordell. ^[1]

Más tarde, Mordell dio una prueba más simple.

 sistema de coordenadas baricéntricas es un sistema de coordenadas en el que la ubicación de un punto de un simplex (un triángulo, tetraedro , etc.) se especifica como el centro de masa , o baricentro, de masas generalmente desiguales colocadas en sus vértices . Las coordenadas también se extienden fuera del símplex, donde una o más coordenadas se vuelven negativas . El sistema fue introducido en 1827 por August Ferdinand Möbius . 

Un 3-simplex, con subdivisiones barcéntricas de 1 caras (bordes) 2 caras (triángulos) y 3 caras (cuerpo).

Definición [ editar ]

Dejar $${\ displaystyle \ mathbf {x} _ {1}, \ ldots, \ mathbf {x} _ {n}}ser los vértices de un simplex en un espacio afín A . Si, por algún punto$${\ displaystyle \ mathbf {p}}en A ,

$${\ displaystyle (a_ {1} + \ cdots + a_ {n}) \ mathbf {p} = a_ {1} \, \ mathbf {x} _ {1} + \ cdots + a_ {n} \, \ mathbf {x} _ {n}}

y al menos uno de $${\ displaystyle a_ {1}, \ ldots, a_ {n}} no desaparece, entonces decimos que los coeficientes ($${\ displaystyle a_ {1}, \ ldots, a_ {n}}) son coordenadas barcéntricas de$${\ displaystyle \ mathbf {p}} con respecto a $${\ displaystyle \ mathbf {x} _ {1}, \ ldots, \ mathbf {x} _ {n}}. Los vértices tienen las coordenadas.$${\ displaystyle \ mathbf {x} _ {1} = (1,0,0, \ ldots, 0), \ mathbf {x} _ {2} = (0,1,0, \ ldots, 0), \ ldots, \ mathbf {x} _ {n} = (0,0,0, \ ldots, 1)}. Las coordenadas barcéntricas no son únicas: para cualquier b que no sea igual a cero, ($${\ displaystyle ba_ {1}, \ ldots, ba_ {n}}) también son coordenadas barcéntricas de p .

Cuando las coordenadas no son negativas, el punto $${\ displaystyle \ mathbf {p}}se encuentra en el casco convexo de$${\ displaystyle \ mathbf {x} _ {1}, \ ldots, \ mathbf {x} _ {n}}, es decir, en el símplex que tiene esos puntos como vértices.

Las coordenadas barcéntricas, como se definieron anteriormente, son una forma de coordenadas homogéneas : de hecho, las coordenadas homogéneas "habituales" son las coordenadas barcéntricas definidas en el espacio n afín extendido en el símplex cuyos vértices son los puntos en el infinito en los ejes de coordenadas, más el origen. Algunas veces los valores de coordenadas están restringidos con una condición

$${\ displaystyle \ sum a_ {i} = 1}

lo que los hace únicos ; entonces, son coordenadas afines . La terminología clásica en este caso es la de las coordenadas barcéntricas absolutas . ^[2]

Coordenadas barcéntricas en triángulos [ editar ]

Esta sección puede ser confusa o poco clara para los lectores . En particular, es innecesariamente técnico y complicado. Por favor, ayúdenos a aclarar la sección . Puede haber una discusión sobre esto en la página de discusión . ( Diciembre de 2018 ) ( Obtenga información sobre cómo y cuándo eliminar este mensaje de plantilla )

Ver también: gráfico ternario y centro triangular

Coordenadas barcéntricas $${\ displaystyle (\ lambda _ {1}, \ lambda _ {2}, \ lambda _ {3})} en un triángulo equilátero y en un triángulo rectángulo.

En el contexto de un triángulo , las coordenadas barcéntricas también se conocen como coordenadas de área o coordenadas de área , porque las coordenadas de P con respecto al triángulo ABC son equivalentes a las relaciones (con signo) de las áreas de PBC , PCA y PAB respecto al área de el triángulo de referencia ABC . Las coordenadas areales y trilineales se usan para propósitos similares en geometría.

Las coordenadas barcéntricas o areales son extremadamente útiles en aplicaciones de ingeniería que involucran subdominios triangulares . Esto hace que las integrales analíticas a menudo sean más fáciles de evaluar, y las tablas de cuadratura gaussianas a menudo se presentan en términos de coordenadas de área.

Considera un triángulo $${\ displaystyle T} definido por sus tres vértices, $${\ displaystyle \ mathbf {r} _ {1}}, $${\ displaystyle \ mathbf {r} _ {2}} y $${\ displaystyle \ mathbf {r} _ {3}}. Cada punto$${\ displaystyle \ mathbf {r}}ubicado dentro de este triángulo se puede escribir como una combinación convexa única de los tres vértices. En otras palabras, para cada$${\ displaystyle \ mathbf {r}} hay una secuencia única de tres números, $${\ displaystyle \ lambda _ {1}, \ lambda _ {2}, \ lambda _ {3} \ geq 0} tal que $${\ displaystyle \ lambda _ {1} + \ lambda _ {2} + \ lambda _ {3} = 1} y

$${\ displaystyle \ mathbf {r} = \ lambda _ {1} \ mathbf {r} _ {1} + \ lambda _ {2} \ mathbf {r} _ {2} + \ lambda _ {3} \ mathbf { r} _ {3},}

Los tres numeros $${\ displaystyle \ lambda _ {1}, \ lambda _ {2}, \ lambda _ {3}} indicar las coordenadas "barcéntricas" o "de área" del punto $${\ displaystyle \ mathbf {r}}con respecto al triangulo. A menudo se denotan como$${\ displaystyle \ alpha, \ beta, \ gamma} en lugar de $${\ displaystyle \ lambda _ {1}, \ lambda _ {2}, \ lambda _ {3}}. Tenga en cuenta que aunque hay tres coordenadas, solo hay dos grados de libertad , ya que$${\ displaystyle \ lambda _ {1} + \ lambda _ {2} + \ lambda _ {3} = 1}. Por lo tanto, cada punto se define de manera única por cualquiera de las dos coordenadas barcéntricas.

Para explicar por qué estas coordenadas son proporciones de áreas con signo , supongamos que trabajamos en el espacio euclidiano.$${\ displaystyle \ mathbf {E} ^ {3}}. Aquí, considere el sistema de coordenadas cartesianas $${\ displaystyle Oxyz}y su base asociada , a saber$${\ displaystyle \ {\ mathbf {i}, \ mathbf {j}, \ mathbf {k} \}}. Considere también el triángulo orientado positivamente $${\ displaystyle ABC} acostado en el $${\ displaystyle Oxy} avión . Se sabe que para cualquier base $${\ displaystyle \ {\ mathbf {e}, \ mathbf {f}, \ mathbf {g} \}} de $${\ displaystyle \ mathbf {E} ^ {3}}y cualquier vector libre $${\ displaystyle \ mathbf {h}}uno tiene ^[3]

$${\ displaystyle \ mathbf {h} = {\ frac {1} {(\ mathbf {e}, \ mathbf {f}, \ mathbf {g})}} \ cdot \ left [(\ mathbf {h}, \ mathbf {f}, \ mathbf {g}) \ mathbf {e} + (\ mathbf {e}, \ mathbf {h}, \ mathbf {g}) \ mathbf {f} + (\ mathbf {e}, \ mathbf {f}, \ mathbf {h}) \ mathbf {g} \ right],}

dónde $${\ displaystyle (\ mathbf {e}, \ mathbf {f}, \ mathbf {g}) = (\ mathbf {e} \ times \ mathbf {f}) \ cdot \ mathbf {g}}representa el producto mixto de estos tres vectores.

Tomar $${\ displaystyle \ mathbf {e} = {\ vec {AB}}, \, \ mathbf {f} = {\ vec {AC}}, \, \ mathbf {g} = \ mathbf {k}, \, \ mathbf {h} = {\ vec {AP}}}, dónde $${\ displaystyle P} es un punto arbitrario en el plano $${\ displaystyle Oxy}y comentar que

$${\ displaystyle (\ mathbf {e}, \ mathbf {f}, \ mathbf {h}) = ({\ vec {AB}} \ times {\ vec {AC}}) \ cdot {\ vec {AP}} = (\ vert {\ vec {AB}} \ times {\ vec {AC}} \ vert \ mathbf {k}) \ cdot {\ vec {AP}} = 0.}

Un punto sutil con respecto a nuestra elección de vectores libres: $${\ displaystyle \ mathbf {e}}es, de hecho, la clase de equipollencia del vector enlazado $${\ displaystyle {\ vec {AB}}}.

Hemos obtenido que

$${\ displaystyle {\ vec {AP}} = m_ {B} \ cdot {\ vec {AB}} + m_ {C} \ cdot {\ vec {AC}}, \, {\ mbox {where}} \, m_ {B} = {\ frac {({\ vec {AP}}, {\ vec {AC}}, \ mathbf {k})} {({\ vec {AB}}, {\ vec {AC}} , \ mathbf {k})}}, \, m_ {C} = {\ frac {({\ vec {AB}}, {\ vec {AP}}, \ mathbf {k})} {({\ vec {AB}}, {\ vec {AC}}, \ mathbf {k})}}.}

Dada la orientación positiva (en sentido antihorario ) del triángulo$${\ displaystyle ABC}, el denominador de ambos$${\ displaystyle m_ {B}} y $${\ displaystyle m_ {C}}es precisamente el doble del área del triángulo $${\ displaystyle ABC}. También,

$${\ displaystyle ({\ vec {AP}}, {\ vec {AC}}, \ mathbf {k}) = ({\ vec {PC}}, {\ vec {PA}}, \ mathbf {k}) \, {\ mbox {y}} \, ({\ vec {AB}}, {\ vec {AP}}, \ mathbf {k}) = ({\ vec {PA}}, {\ vec {PB} }, \ mathbf {k})}

y así los numeradores de$${\ displaystyle m_ {B}} y $${\ displaystyle m_ {C}}son los dobles de las áreas de triángulos con signo$${\ displaystyle APC} y respectivamente $${\ displaystyle ABP}.

Además, deducimos que

$${\ displaystyle {\ vec {OP}} = (1-m_ {B} -m_ {C}) \ cdot {\ vec {OA}} + m_ {B} \ cdot {\ vec {OB}} + m_ { C} \ cdot {\ vec {OC}}}

lo que significa que los números $${\ displaystyle 1-m_ {B} -m_ {C}}, $${\ displaystyle m_ {B}} y $${\ displaystyle m_ {C}} son las coordenadas barcéntricas de $${\ displaystyle P}. Del mismo modo, la tercera coordenada barcéntrica se lee como

$${\ displaystyle m_ {A} = 1-m_ {B} -m_ {C} = {\ frac {({\ vec {PB}}, {\ vec {PC}}, \ mathbf {k})} {( {\ vec {AB}}, {\ vec {AC}}, \ mathbf {k})}}.}

Esta $${\ displaystyle m}-la notación de las coordenadas barcéntricas proviene del hecho de que el punto $${\ displaystyle P}puede ser interpretado como el centro de masa para las masas$${\ displaystyle m_ {A}}, $${\ displaystyle m_ {B}}, $${\ displaystyle m_ {C}} que se encuentran en $${\ displaystyle A}, $${\ displaystyle B} y $${\ displaystyle C}.

Cambiar de ida y vuelta entre las coordenadas barcéntricas y otros sistemas de coordenadas hace que algunos problemas sean mucho más fáciles de resolver.

Conversión entre coordenadas barcéntricas y cartesianas [ editar ]

Dado un punto $${\ displaystyle \ mathbf {r}} en el plano de un triángulo se pueden obtener las coordenadas barcéntricas $${\ displaystyle \ lambda _ {1}}, $${\ displaystyle \ lambda _ {2}} y $${\ displaystyle \ lambda _ {3}}de las coordenadas cartesianas $${\ displaystyle (x, y)} o viceversa.

Podemos escribir las coordenadas cartesianas del punto. $${\ displaystyle \ mathbf {r}} en términos de los componentes cartesianos de los vértices del triángulo $${\ displaystyle \ mathbf {r} _ {1}}, $${\ displaystyle \ mathbf {r} _ {2}}, $${\ displaystyle \ mathbf {r} _ {3}} dónde $${\ displaystyle \ mathbf {r} _ {i} = (x_ {i}, y_ {i})} y en términos de las coordenadas barcéntricas de $${\ displaystyle \ mathbf {r}} como

$${\ displaystyle {\ begin {matrix} x = \ lambda _ {1} x_ {1} + \ lambda _ {2} x_ {2} + \ lambda _ {3} x_ {3} \\ y = \ lambda _ {1} y_ {1} + \ lambda _ {2} y_ {2} + \ lambda _ {3} y_ {3} \\\ end {matriz}}}

Es decir, las coordenadas cartesianas de cualquier punto son un promedio ponderado de las coordenadas cartesianas de los vértices del triángulo, siendo los pesos las coordenadas barcéntricas del punto que suman la unidad.

Para encontrar la transformación inversa, desde coordenadas cartesianas a coordenadas barcéntricas, primero sustituimos $${\ displaystyle \ lambda _ {3} = 1- \ lambda _ {1} - \ lambda _ {2}} en lo anterior para obtener

$${\ displaystyle {\ begin {matrix} x = \ lambda _ {1} x_ {1} + \ lambda _ {2} x_ {2} + (1- \ lambda _ {1} - \ lambda _ {2}) x_ {3} \\ y = \ lambda _ {1} y_ {1} + \ lambda _ {2} y_ {2} + (1- \ lambda _ {1} - \ lambda _ {2}) y_ {3 } \\\ end {matrix}}}

Reorganizando, esto es

$${\ displaystyle {\ begin {matrix} \ lambda _ {1} (x_ {1} -x_ {3}) + \ lambda _ {2} (x_ {2} -x_ {3}) + x_ {3} - x = 0 \\\ lambda _ {1} (y_ {1} -y_ {3}) + \ lambda _ {2} (y_ {2} -y_ {3}) + y_ {3} -y = 0 \ \\ end {matrix}}}

Esta transformación lineal puede escribirse más sucintamente como

$${\ displaystyle \ mathbf {T} \ cdot \ lambda = \ mathbf {r} - \ mathbf {r} _ {3}}

dónde $${\ displaystyle \ lambda}es el vector de las dos primeras coordenadas barcéntricas,$${\ displaystyle \ mathbf {r}}es el vector de coordenadas cartesianas , y$${\ displaystyle \ mathbf {T}}es una matriz dada por

{\ displaystyle \ mathbf {T} = \ left ({\ begin {matrix} x_ {1} -x_ {3} & x_ {2} -x_ {3} \\ y_ {1} -y_ {3} & y_ {2 } -y_ {3} \\\ end {matriz}} \ right)}

Ahora la matriz $${\ displaystyle \ mathbf {T}}es invertible , ya que$${\ displaystyle \ mathbf {r} _ {1} - \ mathbf {r} _ {3}} y $${\ displaystyle \ mathbf {r} _ {2} - \ mathbf {r} _ {3}}son linealmente independientes (si este no fuera el caso, entonces$${\ displaystyle \ mathbf {r} _ {1}}, $${\ displaystyle \ mathbf {r} _ {2}}y $${\ displaystyle \ mathbf {r} _ {3}}sería colineal y no formaría un triángulo). Por lo tanto, podemos reorganizar la ecuación anterior para obtener

$${\ displaystyle \ left ({\ begin {matrix} \ lambda _ {1} \\\ lambda _ {2} \ end {matrix}} \ right) = \ mathbf {T} ^ {- 1} (\ mathbf { r} - \ mathbf {r} _ {3})}

Encontrar las coordenadas barcéntricas se ha reducido así a encontrar la matriz inversa 2 × 2 de$${\ displaystyle \ mathbf {T}}Un problema fácil.

Explícitamente, las fórmulas para las coordenadas barcéntricas del punto $${\ displaystyle \ mathbf {r}}en términos de sus coordenadas cartesianas ( x, y ) y en términos de las coordenadas cartesianas de los vértices del triángulo son:

$${\ displaystyle \ lambda _ {1} = {\ frac {(y_ {2} -y_ {3}) (x-x_ {3}) + (x_ {3} -x_ {2}) (y-y_ { 3})} {\ det (T)}} = {\ frac {(y_ {2} -y_ {3}) (x-x_ {3}) + (x_ {3} -x_ {2}) (y -y_ {3})} {(y_ {2} -y_ {3}) (x_ {1} -x_ {3}) + (x_ {3} -x_ {2}) (y_ {1} -y_ { 3})}} \ ,,}

$${\ displaystyle \ lambda _ {2} = {\ frac {(y_ {3} -y_ {1}) (x-x_ {3}) + (x_ {1} -x_ {3}) (y-y_ { 3})} {\ det (T)}} = {\ frac {(y_ {3} -y_ {1}) (x-x_ {3}) + (x_ {1} -x_ {3}) (y -y_ {3})} {(y_ {2} -y_ {3}) (x_ {1} -x_ {3}) + (x_ {3} -x_ {2}) (y_ {1} -y_ { 3})}} \ ,,}

$${\ displaystyle \ lambda _ {3} = 1- \ lambda _ {1} - \ lambda _ {2} \ ,.}

Otra forma de resolver la conversión de coordenadas cartesianas a barcéntricas es reescribir el problema en forma de matriz para que

$${\ displaystyle \ mathbf {r} = \ mathbf {R} {\ boldsymbol {\ lambda}}}

con $${\ displaystyle \ mathbf {R} = \ left ({\ begin {matrix} \ mathbf {r} _ {1} | \ mathbf {r} _ {2} | \ mathbf {r} _ {3} \ end { matriz}} \ derecha)} y $${\ displaystyle {\ boldsymbol {\ lambda}} = \ left (\ lambda _ {1}, \ lambda _ {2}, \ lambda _ {3} \ right) ^ {\ top}}. Entonces, la condición$${\ displaystyle \ lambda _ {1} + \ lambda _ {2} + \ lambda _ {3} = 1} lee $${\ displaystyle \ left (1,1,1 \ right) {\ boldsymbol {\ lambda}} = 1} y las coordenadas barcéntricas se pueden resolver como la solución del sistema lineal

{\ displaystyle \ left ({\ begin {matrix} x_ {1} & x_ {2} & x_ {3} \\ y_ {1} & y_ {2} & y_ {3} \\ 1 & 1 & 1 \ end {matrix}} \ right) {\ boldsymbol {\ lambda}} = \ left ({\ begin {matrix} x \\ y \\ 1 \ end {matrix}} \ right)}

Conversión entre coordenadas barcéntricas y trilineales [ editar ]

Un punto con coordenadas trilineales x  : y  : z tiene coordenadas barcéntricas ax  : by  : cz donde a , b , c son las longitudes laterales del triángulo. Por el contrario, un punto con barcencéntricos$${\ displaystyle \ lambda _ {1}: \ lambda _ {2}: \ lambda _ {3}} tiene trilineales $${\ displaystyle \ lambda _ {1} / a: \ lambda _ {2} / b: \ lambda _ {3} / c.}

Ecuaciones en coordenadas barcéntricas [ editar ]

Los lados a, b, c tienen respectivamente ecuaciones ^[4]

$${\ displaystyle \ lambda _ {1} = 0, \ quad \ lambda _ {2} = 0, \ quad \ lambda _ {3} = 0.}

La ecuación de la línea de Euler de un triángulo es ^[4]

{\ displaystyle {\ begin {vmatrix} \ lambda _ {1} & \ lambda _ {2} & \ lambda _ {3} \\ 1 & 1 & 1 \\\ tan A & \ tan B & \ tan C \ end {vmatrix}} = 0.}

Usando la conversión dada previamente entre coordenadas baricéntricas y trilineales, las otras ecuaciones dadas en coordenadas trilineales # Las fórmulas se pueden reescribir en términos de coordenadas barcéntricas.

Distancia entre puntos [ editar ]

El vector de desplazamiento de dos puntos normalizados. $${\ displaystyle P = (p_ {1}, p_ {2}, p_ {3})} y $${\ displaystyle Q = (q_ {1}, q_ {2}, q_ {3})}es ^[5]

$${\ displaystyle {\ overrightarrow {PQ}} = (p_ {1} -q_ {1}, p_ {2} -q_ {2}, p_ {3} -q_ {3}).}

La distancia $${\ displaystyle d} Entre $${\ displaystyle P} y $${\ displaystyle Q}o la longitud del vector de desplazamiento $${\ displaystyle {\ overrightarrow {PQ}} = (x, y, z),}es ^[4] [5]

$${\ displaystyle d ^ {2} = \ left | PQ \ right | ^ {2} = - a ^ {2} yz-b ^ {2} zx-c ^ {2} xy = {\ frac {1} { 2}} [x ^ {2} (b ^ {2} + c ^ {2} -a ^ {2}) + y ^ {2} (c ^ {2} + a ^ {2} -b ^ { 2}) + z ^ {2} (a ^ {2} + b ^ {2} -c ^ {2})].}

donde a, b, c son las longitudes laterales del triángulo. La equivalencia de las dos últimas expresiones se deduce de$${\ displaystyle x + y + z = 0,} que vale porque $${\ displaystyle x + y + z = (p_ {1} -q_ {1}) + (p_ {2} -q_ {2}) + (p_ {3} -q_ {3}) = (p_ {1} + p_ {2} + p_ {3}) - (q_ {1} + q_ {2} + q_ {3}) = 1-1 = 0.}

Las coordenadas barcéntricas de un punto se pueden calcular en función de las distancias d _i a los tres vértices de los triángulos resolviendo la ecuación

{\ displaystyle \ left ({\ begin {matrix} -c ^ {2} & c ^ {2} & b ^ {2} -a ^ {2} \\ - b ^ {2} & c ^ {2} -a ^ {2} & b ^ {2} \\ 1 & 1 & 1 \ end {matrix}} \ right) {\ boldsymbol {\ lambda}} = \ left ({\ begin {matrix} d_ {A} ^ {2} -d_ {B } ^ {2} \\ d_ {A} ^ {2} -d_ {C} ^ {2} \\ 1 \ end {matriz}} \ right).}

Aplicaciones [ editar ]

Determinación de la ubicación con respecto a un triángulo [ editar ]

Aunque las coordenadas barcéntricas se usan más comúnmente para manejar puntos dentro de un triángulo, también se pueden usar para describir un punto fuera del triángulo. Si el punto no está dentro del triángulo, entonces todavía podemos usar las fórmulas anteriores para calcular las coordenadas barcéntricas. Sin embargo, dado que el punto está fuera del triángulo, al menos una de las coordenadas violará nuestra suposición original de que$${\ displaystyle \ lambda _ {1 ... 3} \ geq 0}. De hecho, dado cualquier punto en coordenadas cartesianas, podemos usar este hecho para determinar dónde está este punto con respecto a un triángulo.

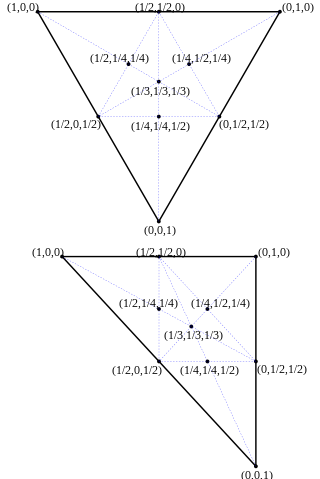
Si un punto se encuentra en el interior del triángulo, todas las coordenadas barcéntricas se encuentran en el intervalo abierto $${\ displaystyle (0,1).} Si un punto se encuentra en un borde del triángulo pero no en un vértice, una de las coordenadas del área $${\ displaystyle \ lambda _ {1 ... 3}} (el asociado con el vértice opuesto) es cero, mientras que los otros dos se encuentran en el intervalo abierto $${\ displaystyle (0,1).}Si el punto se encuentra en un vértice, la coordenada asociada con ese vértice es igual a 1 y las demás son iguales a cero. Finalmente, si el punto se encuentra fuera del triángulo, al menos una coordenada es negativa.

Resumiendo

Punto $${\ displaystyle \ mathbf {r}}se encuentra dentro del triángulo si y solo si {\ displaystyle 0 <\ lambda _ {i} <1 font="" forall="" i="" in="" text="">.

$${\ displaystyle \ mathbf {r}} se encuentra en el borde o la esquina del triángulo si $${\ displaystyle 0 \ leq \ lambda _ {i} \ leq 1 \; \ forall \; i {\ text {in}} {1,2,3}} y $${\ displaystyle \ lambda _ {i} = 0 \; {\ text {, para algunos i in}} {1,2,3}}.

De otra manera, $${\ displaystyle \ mathbf {r}} Se encuentra fuera del triángulo.

En particular, si un punto se encuentra en el lado opuesto de una línea lateral desde el vértice opuesto a esa línea lateral, entonces la coordenada barcéntrica de ese punto correspondiente a ese vértice es negativa.

Interpolación en una cuadrícula triangular no estructurada [ editar ]

Superficie (parte superior) obtenida de la interpolación lineal sobre una cuadrícula triangular dada (parte inferior) en el plano x , y . La superficie se aproxima a una función z = f ( x , y ), dados solo los valores de f en los vértices de la cuadrícula.

Si $${\ displaystyle f (\ mathbf {r} _ {1}), f (\ mathbf {r} _ {2}), f (\ mathbf {r} _ {3})} son cantidades conocidas, pero los valores de $${\ displaystyle f} dentro del triángulo definido por $${\ displaystyle \ mathbf {r} _ {1}, \ mathbf {r} _ {2}, \ mathbf {r} _ {3}}es desconocido, se pueden aproximar mediante interpolación lineal . Las coordenadas barcéntricas proporcionan una forma conveniente de calcular esta interpolación. Si$${\ displaystyle \ mathbf {r}} es un punto dentro del triángulo con coordenadas barcéntricas $${\ displaystyle \ lambda _ {1}}, $${\ displaystyle \ lambda _ {2}}, $${\ displaystyle \ lambda _ {3}}, luego

$${\ displaystyle f (\ mathbf {r}) \ approx \ lambda _ {1} f (\ mathbf {r} _ {1}) + \ lambda _ {2} f (\ mathbf {r} _ {2}) + \ lambda _ {3} f (\ mathbf {r} _ {3})}

En general, dada cualquier cuadrícula no estructurada o malla poligonal , este tipo de técnica se puede utilizar para aproximar el valor de$${\ displaystyle f}en todos los puntos, siempre que el valor de la función sea conocido en todos los vértices de la malla. En este caso, tenemos muchos triángulos, cada uno correspondiente a una parte diferente del espacio. Interpolar una función.$${\ displaystyle f} en un punto $${\ displaystyle \ mathbf {r}}, primero se debe encontrar un triángulo que contenga $${\ displaystyle \ mathbf {r}}. Para hacerlo$${\ displaystyle \ mathbf {r}}se transforma en las coordenadas barcéntricas de cada triángulo. Si se encuentra algún triángulo tal que las coordenadas satisfagan$${\ displaystyle 0 \ leq \ lambda _ {i} \ leq 1 \; \ forall \; i {\ text {in}} 1,2,3}, entonces el punto se encuentra en ese triángulo o en su borde (explicado en la sección anterior). Entonces el valor de$${\ displaystyle f (\ mathbf {r})} se puede interpolar como se describió anteriormente.

Estos métodos tienen muchas aplicaciones, como el método de elementos finitos (FEM).

Integración sobre un triángulo [ editar ]

La integral de una función sobre el dominio del triángulo puede ser molesta para calcular en un sistema de coordenadas cartesianas. Generalmente hay que dividir el triángulo en dos mitades, y sigue un gran desorden. En cambio, a menudo es más fácil hacer un cambio de variables a cualquiera de las dos coordenadas barcéntricas, p. Ej.$${\ displaystyle \ lambda _ {1}, \ lambda _ {2}}. Bajo este cambio de variables,

$${\ displaystyle \ int _ {T} f (\ mathbf {r}) \ d \ mathbf {r} = 2A \ int _ {0} ^ {1} \ int _ {0} ^ {1- \ lambda _ { 2}} f (\ lambda _ {1} \ mathbf {r} _ {1} + \ lambda _ {2} \ mathbf {r} _ {2} + (1- \ lambda _ {1} - \ lambda _ {2}) \ mathbf {r} _ {3}) \ d \ lambda _ {1} \ d \ lambda _ {2}}

dónde $${\ displaystyle A}es el área del triángulo Este resultado se deduce del hecho de que un rectángulo en coordenadas barcéntricas corresponde a un cuadrilátero en coordenadas cartesianas, y la relación de las áreas de las formas correspondientes en los sistemas de coordenadas correspondientes está dada por$${\ displaystyle 2A}.

Ejemplos de puntos especiales [ editar ]

Los tres vértices de un triángulo tienen coordenadas barcéntricas.$${\ displaystyle 1: 0: 0, \ quad 0: 1: 0, \ quad {\ text {y}} \ quad 0: 0: 1.}^[4]

El centroide tiene barcéntricos.$${\ displaystyle 1: 1: 1.}^[4]

El circuncentro de un triángulo ABC tiene coordenadas barcéntricas ^{[4] [5] [6] [7]}

$${\ displaystyle a ^ {2} (- a ^ {2} + b ^ {2} + c ^ {2}): \; b ^ {2} (a ^ {2} -b ^ {2} + c ^ {2}): \; c ^ {2} (a ^ {2} + b ^ {2} -c ^ {2})}

$${\ displaystyle = \ sin 2A: \ sin 2B: \ sin 2C = (1- \ cos B \ cos C) :( 1- \ cos C \ cos A) :( 1- \ cos A \ cos B).}

donde a , b , c son longitudes de borde BC , CA , AB respectivamente del triángulo.

El ortocentro tiene coordenadas barcéntricas ^[4] [5]

$${\ displaystyle (a ^ {2} + b ^ {2} -c ^ {2}) (a ^ {2} -b ^ {2} + c ^ {2}): \; (- a ^ {2 } + b ^ {2} + c ^ {2}) (a ^ {2} + b ^ {2} -c ^ {2}): \; (a ^ {2} -b ^ {2} + c ^ {2}) (- a ^ {2} + b ^ {2} + c ^ {2})}

$${\ displaystyle = \ tan A: \ tan B: \ tan C = a \ cos B \ cos C: b \ cos C \ cos A: c \ cos A \ cos B.}

El incentro tiene coordenadas barcéntricas ^[5] [8]

$${\ displaystyle a: b: c = \ sin A: \ sin B: \ sin C.}

Los excentros barycentrics 'son ^[8]

$${\ displaystyle -a: b: c \ quad \ quad a: -b: c \ quad \ quad a: b: -c.}

El centro de nueve puntos tiene coordenadas barcéntricas ^[4] [8]

$${\ displaystyle a \ cos (BC): b \ cos (CA): c \ cos (AB) = (1+ \ cos B \ cos C) :( 1+ \ cos C \ cos A) :( 1+ \ cos A \ cos B)}

$${\ displaystyle = [a ^ {2} (b ^ {2} + c ^ {2}) - (b ^ {2} -c ^ {2}) ^ {2}]: [b ^ {2} ( c ^ {2} + a ^ {2}) - (c ^ {2} -a ^ {2}) ^ {2}]: [c ^ {2} (a ^ {2} + b ^ {2} ) - (a ^ {2} -b ^ {2}) ^ {2}].}

Coordenadas barcéntricas en tetraedros [ editar ]

Las coordenadas barcéntricas pueden extenderse fácilmente a tres dimensiones . El 3D simplex es un tetraedro , un poliedro que tiene cuatro caras triangulares y cuatro vértices. Una vez más, las coordenadas barcéntricas se definen de modo que el primer vértice$${\ displaystyle \ mathbf {r} _ {1}} mapas a coordenadas barcéntricas $${\ displaystyle \ lambda = (1,0,0,0)}, $${\ displaystyle \ mathbf {r} _ {2} \ to (0,1,0,0)}etc.

Esto es nuevamente una transformación lineal, y podemos extender el procedimiento anterior para triángulos para encontrar las coordenadas barcéntricas de un punto $${\ displaystyle \ mathbf {r}} con respecto a un tetraedro:

$${\ displaystyle \ left ({\ begin {matrix} \ lambda _ {1} \\\ lambda _ {2} \\\ lambda _ {3} \ end {matrix}} \ right) = \ mathbf {T} ^ {-1} (\ mathbf {r} - \ mathbf {r} _ {4})}

dónde $${\ displaystyle \ mathbf {T}} ahora es una matriz 3 × 3:

{\ displaystyle \ mathbf {T} = \ left ({\ begin {matrix} x_ {1} -x_ {4} & x_ {2} -x_ {4} & x_ {3} -x_ {4} \\ y_ {1 } -y_ {4} y y_ {2} -y_ {4} y y_ {3} -y_ {4} \\ z_ {1} -z_ {4} y z_ {2} -z_ {4} y z_ {3} -z_ {4} \ end {matrix}} \ right)}

Una vez más, el problema de encontrar las coordenadas barcéntricas se ha reducido a invertir una matriz de 3 × 3. Las coordenadas barcéntricas 3D se pueden usar para decidir si un punto se encuentra dentro de un volumen tetraédrico, y para interpolar una función dentro de una malla tetraédrica, de manera análoga al procedimiento 2D. Las mallas tetraédricas se usan a menudo en el análisis de elementos finitos porque el uso de coordenadas barcéntricas puede simplificar enormemente la interpolación 3D.

Coordenadas barcéntricas generalizadas [ editar ]

Esta sección no cita ninguna fuente . Por favor, ayuda a mejorar esta sección mediante la adición de citas de fuentes confiables . El material sin fuente puede ser cuestionado y eliminado . Buscar fuentes:  "Sistema de coordenadas barcéntricas"  -  noticias  · periódicos  · libros  · erudito  · JSTOR ( diciembre de 2010 ) ( Aprenda cómo y cuándo eliminar este mensaje de plantilla )

Las coordenadas barcéntricas ( a ₁ , ..., a _n ) que se definen con respecto a un politopo en lugar de un simplex se denominan coordenadas barcéntricas generalizadas . Para estos, la ecuación

$${\ displaystyle (a_ {1} + \ cdots + a_ {n}) p = a_ {1} x_ {1} + \ cdots + a_ {n} x_ {n}}

todavía se requiere para mantener donde x ₁ , ..., x _n son los vértices del politopo dado. Por lo tanto, la definición no ha cambiado formalmente, pero si bien un símplex con n vértices debe incrustarse en un espacio vectorial de dimensión de al menos n-1 , un politopo puede incrustarse en un espacio vectorial de dimensión inferior. El ejemplo más simple es un cuadrilátero en el plano. En consecuencia, incluso las coordenadas barcéntricas generalizadas normalizadas (es decir, coordenadas tales que la suma de los coeficientes es 1) en general ya no se determinan de manera única, mientras que este es el caso de las coordenadas barcéntricas normalizadas con respecto a un simplex.

De manera más abstracta, las coordenadas barcéntricas generalizadas expresan un politopo con n vértices, independientemente de la dimensión, como la imagen del estándar.$${\ displaystyle (n-1)}-simplex, que tiene n vértices - el mapa está en:$${\ displaystyle \ Delta ^ {n-1} \ twoheadrightarrow P.}El mapa es uno a uno si y solo si el politopo es un símplex, en cuyo caso el mapa es un isomorfismo; esto corresponde a un punto que no tiene coordenadas barcéntricas generalizadas únicas, excepto cuando P es un simplex.

Las coordenadas barcéntricas duales a generalizadas son variables de holgura , que miden por la cantidad de margen que un punto satisface las restricciones lineales, y da una inserción $${\ displaystyle P \ hookrightarrow (\ mathbf {R} _ {\ geq 0}) ^ {f}}en f - orthant , donde f es el número de caras (duales a los vértices). Este mapa es uno a uno (las variables de holgura se determinan de manera única) pero no en (no se pueden realizar todas las combinaciones).

Este uso del estándar $${\ displaystyle (n-1)}-simplex yf -orthant como objetos estándar que se asignan a un politopo o que un politopo se debe contrastar con el uso del espacio vectorial estándar$${\ displaystyle K ^ {n}}como el objeto estándar para espacios vectoriales y el hiperplano afín estándar $${\ displaystyle \ {(x_ {0}, \ ldots, x_ {n}) \ mid \ sum x_ {i} = 1 \} \ subconjunto K ^ {n + 1}}como el objeto estándar para espacios afines, donde en cada caso elegir una base lineal o una base afín proporciona un isomorfismo, permitiendo que todos los espacios vectoriales y espacios afines se piensen en términos de estos espacios estándar, en lugar de un sobre o uno a un mapa (no todos los politopos son simples). Además, el n -orthant es el objeto estándar que se asigna a los conos.

Aplicaciones [ editar ]

Las coordenadas barcéntricas generalizadas tienen aplicaciones en gráficos de computadora y más específicamente en modelado geométrico . A menudo, un modelo tridimensional puede ser aproximado por un poliedro de modo que las coordenadas barcéntricas generalizadas con respecto a ese poliedro tengan un significado geométrico. De esta manera, el procesamiento del modelo puede simplificarse mediante el uso de estas coordenadas significativas. Las coordenadas barcéntricas también se usan en geofísica