CRIPTOGRAFÍA

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Estándar de cifrado avanzado
(Rijndael)

El paso SubBytes , una de las cuatro etapas en una ronda de AES
General
Diseñadores	Vincent Rijmen , Joan Daemen
Publicado por primera vez	1998
Derivado de	Cuadrado
Sucesores	Anubis , Grand Cru , Kalyna
Certificación	Ganador de AES , CRYPTREC , NESSIE , NSA
Detalle de cifrado
Tamaños clave	128, 192 o 256 bits [nota 1]
Tamaños de bloque	128 bits [nota 2]
Estructura	Red de sustitución-permutación
Rondas	10, 12 o 14 (según el tamaño de la clave)
El mejor criptoanálisis público
Se han publicado ataques que son computacionalmente más rápidos que un ataque de fuerza bruta total , aunque ninguno a partir de 2013 es computacionalmente factible. [1] Para AES-128, la clave se puede recuperar con una complejidad computacional de 2 126.1 utilizando el ataque biclique . Para los ataques bicliques en AES-192 y AES-256, se aplican las complejidades computacionales de 2 189.7 y 2 254.4 respectivamente. Los ataques de teclas relacionadas pueden romper AES-192 y AES-256 con complejidades 2 176 y 2 99.5 en tiempo y datos, respectivamente. [2]

El Advanced Encryption Standard ( AES ), también conocido por su nombre original Rijndael ( pronunciación holandesa: [ˈrɛindaːl] ), ^[3] es una especificación para el cifrado de datos electrónicos establecida por el Instituto Nacional de Estándares y Tecnología de EE. UU. (NIST) en 2001. ^[4]

AES es un subconjunto del cifrado de bloque Rijndael ^[3] desarrollado por dos criptógrafos belgas , Vincent Rijmen y Joan Daemen , que presentaron una propuesta ^[5] a NIST durante el proceso de selección de AES . ^[6] Rijndael es una familia de cifrados con diferentes tamaños de clave y bloque.

Para AES, NIST seleccionó tres miembros de la familia Rijndael, cada uno con un tamaño de bloque de 128 bits, pero tres longitudes de clave diferentes: 128, 192 y 256 bits.

AES ha sido adoptado por el gobierno de los Estados Unidos y ahora se usa en todo el mundo. Reemplaza el Estándar de cifrado de datos (DES), ^[7] que se publicó en 1977. El algoritmo descrito por AES es un algoritmo de clave simétrica , lo que significa que se utiliza la misma clave para cifrar y descifrar los datos.

En los Estados Unidos, el NIST anunció AES como US FIPS PUB 197 (FIPS 197) el 26 de noviembre de 2001. ^[4] Este anuncio siguió a un proceso de estandarización de cinco años en el que se presentaron y evaluaron quince diseños competitivos, antes de El cifrado Rijndael se seleccionó como el más adecuado (consulte el proceso del Estándar de cifrado avanzado para obtener más detalles).

AES entró en vigencia como estándar del gobierno federal el 26 de mayo de 2002, luego de la aprobación del Secretario de Comercio . AES está incluido en el estándar ISO / IEC 18033-3 . AES está disponible en muchos paquetes de cifrado diferentes, y es el primer (y único) cifrado de acceso público aprobado por la Agencia de Seguridad Nacional (NSA) para obtener información secreta cuando se utiliza en un módulo criptográfico aprobado por la NSA (ver Seguridad de AES , a continuación).

Estándares definitivos [ editar ]

El Estándar de cifrado avanzado (AES) se define en cada uno de:

• FIPS PUB 197: Estándar de cifrado avanzado (AES) ^[4]
• ISO / IEC 18033-3 :: Cifrados de bloque ^[8]

Descripción de los cifrados [ editar ]

AES se basa en un principio de diseño conocido como red de sustitución-permutación , y es eficiente tanto en software como en hardware. ^[9] A diferencia de su predecesor DES, AES no utiliza una red Feistel . AES es una variante de Rijndael que tiene un tamaño de bloque fijo de 128 bits y un tamaño de clave de 128, 192 o 256 bits. Por el contrario, Rijndael per se se especifica con tamaños de bloque y clave que pueden ser cualquier múltiplo de 32 bits, con un mínimo de 128 y un máximo de 256 bits.

AES opera en una matriz de bytes de orden principal de columna 4 × 4 , denominada estado . ^{[nota 3]} La mayoría de los cálculos de AES se realizan en un campo finito particular .

Por ejemplo, si hay 16 bytes, $${\ displaystyle b_ {0}, b_ {1}, ..., b_ {15}}, estos bytes se representan como esta matriz bidimensional:

{\ displaystyle {\ begin {bmatrix} b_ {0} & b_ {4} & b_ {8} & b_ {12} \\ b_ {1} & b_ {5} & b_ {9} & b_ {13} \\ b_ {2} y b_ {6} y b_ {10} y b_ {14} \\ b_ {3} y b_ {7} y ​​b_ {11} y b_ {15} \ end {bmatrix}}}

El tamaño de clave utilizado para un cifrado AES especifica el número de rondas de transformación que convierten la entrada, llamada texto sin formato , en la salida final, llamada texto cifrado . El número de rondas es el siguiente:

• 10 rondas para claves de 128 bits.
• 12 rondas para claves de 192 bits.
• 14 rondas para claves de 256 bits.

Cada ronda consta de varios pasos de procesamiento, incluido uno que depende de la clave de cifrado en sí. Se aplica un conjunto de rondas inversas para transformar el texto cifrado nuevamente en el texto sin formato original utilizando la misma clave de cifrado.

Descripción de alto nivel del algoritmo [ editar ]

1. KeyExpansion: las claves redondas se derivan de la clave de cifrado utilizando el programa de claves de Rijndael . AES requiere un bloque de teclas redondo de 128 bits por separado para cada ronda más uno más.
2. Adición de llave redonda inicial:
   1. AddRoundKey: cada byte del estado se combina con un byte de la tecla redonda utilizando bitor xor .
3. 9, 11 o 13 rondas:
   1. SubBytes: un paso de sustitución no lineal donde cada byte se reemplaza por otro de acuerdo con una tabla de búsqueda .
   2. ShiftRows: un paso de transposición donde las últimas tres filas del estado se desplazan cíclicamente un cierto número de pasos.
   3. MixColumns: una operación de mezcla lineal que opera en las columnas del estado, combinando los cuatro bytes en cada columna.
   4. AddRoundKey
4. Ronda final (haciendo 10, 12 o 14 rondas en total):
   1. Subbytes
   2. ShiftRows
   3. AddRoundKey

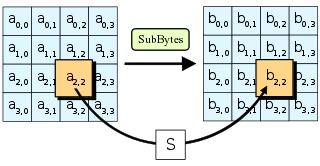
El paso SubBytes [ editar ]

Artículo principal: Rijndael S-box

En el paso SubBytes , cada byte en el estado se reemplaza con su entrada en una tabla de búsqueda fija de 8 bits, S ; b _ij = S (a _ij ) .

En el paso SubBytes , cada byte$${\ displaystyle a_ {i, j}}en la matriz de estado se reemplaza con un SubByte $${\ displaystyle S (a_ {i, j})}utilizando una caja de sustitución de 8 bits . Esta operación proporciona la no linealidad en el cifrado . La caja S utilizada se deriva del inverso multiplicativo sobre GF (2 ⁸ ) , conocido por tener buenas propiedades de no linealidad. Para evitar ataques basados ​​en propiedades algebraicas simples, la caja S se construye combinando la función inversa con una transformación afín invertible . El S-box también se elige para evitar puntos fijos (y por lo tanto es un trastorno ), es decir,$${\ displaystyle S (a_ {i, j}) \ neq a_ {i, j}}, y también cualquier punto fijo opuesto, es decir, $${\ displaystyle S (a_ {i, j}) \ oplus a_ {i, j} \ neq {\ text {FF}} _ {16}}. Al realizar el descifrado, se usa el paso InvSubBytes (el inverso de SubBytes ), que requiere primero tomar el inverso de la transformación afín y luego encontrar el inverso multiplicativo.

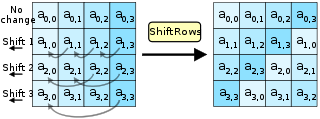
El paso ShiftRows [ editar ]

En el paso ShiftRows , los bytes en cada fila del estado se desplazan cíclicamente a la izquierda. El número de lugares que se desplaza cada byte difiere para cada fila.

El paso ShiftRows opera en las filas del estado; desplaza cíclicamente los bytes en cada fila en un cierto desplazamiento . Para AES, la primera fila no se modifica. Cada byte de la segunda fila se desplaza uno a la izquierda. Del mismo modo, las filas tercera y cuarta se desplazan por desplazamientos de dos y tres respectivamente. ^{[nota 4]} De esta manera, cada columna del estado de salida del paso ShiftRows está compuesta de bytes de cada columna del estado de entrada. La importancia de este paso es evitar que las columnas se cifren de forma independiente, en cuyo caso AES degenera en cuatro cifrados de bloque independientes.

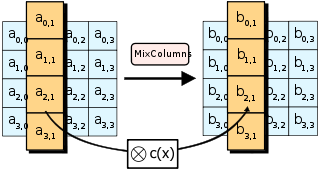
El paso MixColumns [ editar ]

Artículo principal: Rijndael MixColumns

En el paso MixColumns , cada columna del estado se multiplica por un polinomio fijo.$${\ displaystyle c (x)}.

En el paso MixColumns , los cuatro bytes de cada columna del estado se combinan mediante una transformación lineal invertible . La función MixColumns toma cuatro bytes como entrada y genera cuatro bytes, donde cada byte de entrada afecta a los cuatro bytes de salida. Junto con ShiftRows , MixColumns proporciona difusión en el cifrado.

Durante esta operación, cada columna se transforma utilizando una matriz fija (la matriz multiplicada a la izquierda por la columna da un nuevo valor de columna en el estado):

{\ displaystyle {\ begin {bmatrix} b_ {0, j} \\ b_ {1, j} \\ b_ {2, j} \\ b_ {3, j} \ end {bmatrix}} = {\ begin { bmatrix} 2 y 3 y 1 y 1 \\ 1 y 2 y 3 y 1 \\ 1 y 1 y 2 y 3 \\ 3 y 1 y 1 y 2 \ end {bmatrix}} {\ begin {bmatrix} a_ {0, j} \\ a_ {1, j} \\ a_ {2, j} \\ a_ { 3, j} \ end {bmatrix}} \ qquad 0 \ leq j \ leq 3}

La multiplicación matricial se compone de la multiplicación y la suma de las entradas. Las entradas son bytes de 8 bits tratados como coeficientes de polinomio de orden$${\ displaystyle x ^ {7}}. La suma es simplemente XOR. La multiplicación es un módulo polinomio irreducible$${\ displaystyle x ^ {8} + x ^ {4} + x ^ {3} + x + 1}. Si se procesa bit a bit, entonces, después del desplazamiento, se debe realizar un XOR condicional con 1B ₁₆ si el valor desplazado es mayor que FF ₁₆ (el desbordamiento debe corregirse restando el polinomio generador). Estos son casos especiales de la multiplicación habitual en$${\ displaystyle \ operatorname {GF} (2 ^ {8})}.

En un sentido más general, cada columna se trata como un polinomio sobre $${\ displaystyle \ operatorname {GF} (2 ^ {8})} y luego se multiplica el módulo $${\ displaystyle {01} _ {16} \ cdot z ^ {4} + {01} _ {16}} con un polinomio fijo $${\ displaystyle c (z) = {03} _ {16} \ cdot z ^ {3} + {01} _ {16} \ cdot z ^ {2} + {01} _ {16} \ cdot z + {02 }_{dieciséis}}. Los coeficientes se muestran en su equivalente hexadecimal de la representación binaria de los polinomios de bits de$${\ displaystyle \ operatorname {GF} (2) [x]}. El paso MixColumns también se puede ver como una multiplicación por la matriz MDS particular que se muestra en el campo finito $${\ displaystyle \ operatorname {GF} (2 ^ {8})}. Este proceso se describe más detalladamente en el artículo Rijndael MixColumns .

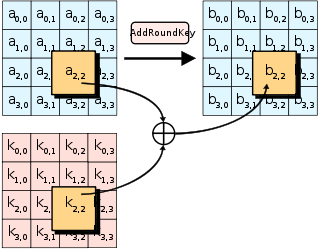
El paso AddRoundKey [ editar ]

En el paso AddRoundKey , cada byte del estado se combina con un byte de la subclave redonda utilizando la operación XOR (⊕).

En el paso AddRoundKey , la subclave se combina con el estado. Para cada ronda, se deriva una subclave de la clave principal utilizando el programa de claves de Rijndael ; cada subclave tiene el mismo tamaño que el estado. La subclave se agrega combinando cada byte del estado con el byte correspondiente de la subclave usando XOR bit a bit .

Optimización del cifrado [ editar ]

En sistemas con palabras de 32 bits o más grandes, es posible acelerar la ejecución de este cifrado combinando los pasos SubBytes y ShiftRows con el paso MixColumns transformándolos en una secuencia de búsquedas en la tabla. Esto requiere cuatro tablas de 32 bits de 256 entradas (que en conjunto ocupan 4096 bytes). Luego se puede realizar una ronda con 16 operaciones de búsqueda en la tabla y 12 operaciones exclusivas u de 32 bits, seguidas de cuatro operaciones exclusivas u de 32 bits en el paso AddRoundKey . ^[10] Alternativamente, la operación de búsqueda de la tabla se puede realizar con una sola tabla de 32 bits de 256 entradas (que ocupa 1024 bytes) seguida de operaciones de rotación circular.

Usando un enfoque orientado a bytes, es posible combinar los pasos SubBytes , ShiftRows y MixColumns en una sola operación de ronda. ^[11]

Seguridad [ editar ]

La Agencia de Seguridad Nacional (NSA) revisó a todos los finalistas de AES, incluido Rijndael, y declaró que todos ellos eran lo suficientemente seguros para los datos no clasificados del gobierno de EE. En junio de 2003, el gobierno de EE. UU. Anunció que AES podría utilizarse para proteger la información clasificada :

El diseño y la fuerza de todas las longitudes de clave del algoritmo AES (es decir, 128, 192 y 256) son suficientes para proteger la información clasificada hasta el nivel SECRETO. La información TOP SECRET requerirá el uso de las longitudes de clave 192 o 256. La implementación de AES en productos destinados a proteger los sistemas y / o la información de seguridad nacional debe ser revisada y certificada por la NSA antes de su adquisición y uso. ^[12]

AES tiene 10 rondas para claves de 128 bits, 12 rondas para claves de 192 bits y 14 rondas para claves de 256 bits.

En 2006, los ataques más conocidos fueron 7 rondas para claves de 128 bits, 8 rondas para claves de 192 bits y 9 rondas para claves de 256 bits. ^[13]

Ataques conocidos [ editar ]

Para los criptógrafos, una "ruptura" criptográfica es algo más rápido que un ataque de fuerza bruta , es decir, realizar un descifrado de prueba para cada clave posible en secuencia (ver Criptoanálisis ). Un descanso puede incluir resultados que no son factibles con la tecnología actual. A pesar de no ser práctico, los descansos teóricos a veces pueden proporcionar información sobre los patrones de vulnerabilidad. El mayor ataque exitoso de fuerza bruta conocido públicamente contra un algoritmo de cifrado de cifrado en bloque ampliamente implementado fue contra una clave RC5 de 64 bits por distribuido.net en 2006. ^[14]

El espacio de la clave aumenta en un factor de 2 por cada bit adicional de longitud de la clave, y si cada valor posible de la clave es equiprobable, esto se traduce en una duplicación del tiempo promedio de búsqueda de la clave de fuerza bruta. Esto implica que el esfuerzo de una búsqueda de fuerza bruta aumenta exponencialmente con la longitud de la clave. La longitud de la clave en sí misma no implica seguridad contra ataques, ya que hay cifrados con claves muy largas que se han encontrado vulnerables.

AES tiene un marco algebraico bastante simple. ^[15] En 2002, Nicolas Courtois y Josef Pieprzyk anunciaron un ataque teórico, llamado " ataque XSL ", que pretendía mostrar una debilidad en el algoritmo AES, en parte debido a la baja complejidad de sus componentes no lineales. ^[16] Desde entonces, otros documentos han demostrado que el ataque, como se presentó originalmente, es inviable; ver ataque XSL en cifrados de bloque .

Durante el proceso de selección de AES, los desarrolladores de algoritmos competidores escribieron sobre el algoritmo de Rijndael "... nos preocupa [su] uso ... en aplicaciones críticas para la seguridad". ^[17] En octubre de 2000, sin embargo, al final del El proceso de selección de AES, Bruce Schneier , desarrollador del algoritmo de la competencia Twofish , escribió que si bien pensaba que algún día se desarrollarían ataques académicos exitosos en Rijndael, no "creía que alguien descubriera un ataque que permita a alguien leer el tráfico de Rijndael". . ” ^[18]

Hasta mayo de 2009, los únicos ataques publicados exitosos contra el AES completo fueron ataques de canal lateral en algunas implementaciones específicas. En 2009, se descubrió un nuevo ataque de clave relacionada que explota la simplicidad de la programación clave de AES y tiene una complejidad de 2 ¹¹⁹ . En diciembre de 2009 se mejoró a 2 ^99.5 . ^[2] Este es un seguimiento de un ataque descubierto a principios de 2009 por Alex Biryukov , Dmitry Khovratovich e Ivica Nikolić, con una complejidad de 2 ⁹⁶ por una de cada 2 ³⁵ teclas. ^[19]Sin embargo, los ataques de claves relacionadas no son motivo de preocupación en ningún protocolo criptográfico diseñado adecuadamente, ya que un protocolo diseñado adecuadamente (es decir, un software de implementación) se ocupará de no permitir claves relacionadas, esencialmente restringiendo los medios de un atacante para seleccionar claves para la relación.

Bruce Schneier ^[20] escribió otro blog el 30 de julio de 2009 y lo lanzó como preimpresión ^[21] el 3 de agosto de 2009. Este nuevo ataque, de Alex Biryukov, Orr Dunkelman, Nathan Keller, Dmitry Khovratovich y Adi Shamir , está en contra de AES-256 que usa solo dos claves relacionadas y 2 ³⁹ veces para recuperar la clave completa de 256 bits de una versión de 9 rondas, o 2 ⁴⁵ veces para una versión de 10 rondas con un tipo más fuerte de ataque de subclave relacionado, o 2 ⁷⁰ veces para una versión de 11 rondas. AES de 256 bits usa 14 rondas, por lo que estos ataques no son efectivos contra AES completo.

La practicidad de estos ataques con claves relacionadas más fuertes ha sido criticada, ^[22] por ejemplo, por el artículo sobre los ataques de "relaciones clave elegidas en el medio" contra AES-128 escrito por Vincent Rijmen en 2010. ^{[23] ]}

En noviembre de 2009, el primer ataque distintivo de clave conocida contra una versión reducida de 8 rondas de AES-128 se lanzó como preimpresión. ^[24] Este ataque distintivo de clave conocida es una mejora del rebote, o el ataque de inicio desde el medio, contra permutaciones similares a AES, que ven dos rondas consecutivas de permutación como la aplicación de un llamado Super- Sbox Funciona en la versión de 8 rondas de AES-128, con una complejidad de tiempo de 2 ⁴⁸ y una complejidad de memoria de 2 ³² . AES de 128 bits usa 10 rondas, por lo que este ataque no es efectivo contra AES-128 completo.

Los primeros ataques de recuperación de claves en AES completo se debieron a Andrey Bogdanov, Dmitry Khovratovich y Christian Rechberger, y se publicaron en 2011. ^[25] El ataque es un ataque biclique y es más rápido que la fuerza bruta en un factor de aproximadamente cuatro. Se requieren 2 ^126.2 operaciones para recuperar una clave AES-128. Para AES-192 y AES-256, se necesitan 2 ^190.2 y 2 ^254.6 operaciones, respectivamente. Este resultado se ha mejorado aún más a 2 ^126.0 para AES-128, 2 ^189.9 para AES-192 y 2 ^254.3 para AES-256, ^[26] que son los mejores resultados actuales en el ataque de recuperación clave contra AES.

Esta es una ganancia muy pequeña, ya que una clave de 126 bits (en lugar de 128 bits) todavía tomaría miles de millones de años para aplicar la fuerza bruta en el hardware actual y previsible. Además, los autores calculan que el mejor ataque utilizando su técnica en AES con una clave de 128 bits requiere almacenar 2 ⁸⁸ bits de datos. Eso equivale a unos 38 billones de terabytes de datos, que es más que todos los datos almacenados en todas las computadoras del planeta en 2016. Como tal, no hay implicaciones prácticas en la seguridad de AES. ^[27] La complejidad del espacio se ha mejorado más tarde a 2 ⁵⁶ bits, ^[26] que es 9007 terabytes.

Según los documentos de Snowden , la NSA está investigando si un ataque criptográfico basado en la estadística tau puede ayudar a romper el AES. ^[28]

En la actualidad, no se conoce ningún ataque práctico que permita a alguien sin conocimiento de la clave leer los datos cifrados por AES cuando se implementa correctamente.

Ataques de canal lateral [ editar ]

Los ataques de canal lateral no atacan el cifrado como una caja negra y, por lo tanto, no están relacionados con la seguridad del cifrado como se define en el contexto clásico, pero son importantes en la práctica. Atacan implementaciones del cifrado en sistemas de hardware o software que filtran datos inadvertidamente. Existen varios ataques conocidos en diversas implementaciones de AES.

En abril de 2005, DJ Bernstein anunció un ataque de sincronización de caché que usó para romper un servidor personalizado que usaba el cifrado AES de OpenSSL . ^[29] El ataque requirió más de 200 millones de textos claros elegidos. ^[30] El servidor personalizado fue diseñado para proporcionar la mayor cantidad de información de temporización posible (el servidor informa el número de ciclos de la máquina tomados por la operación de cifrado). Sin embargo, como señaló Bernstein, "reducir la precisión de las marcas de tiempo del servidor, o eliminarlas de las respuestas del servidor, no detiene el ataque: el cliente simplemente usa los tiempos de ida y vuelta en función de su reloj local y compensa el aumento de ruido promediando un mayor número de muestras ". ^[29]

En octubre de 2005, Dag Arne Osvik, Adi Shamir y Eran Tromer presentaron un documento que demuestra varios ataques de temporización de caché contra las implementaciones en AES que se encuentran en OpenSSL y la dm-cryptfunción de cifrado de particiones de Linux . ^[31] Un ataque pudo obtener una clave AES completa después de solo 800 operaciones que desencadenaron cifrados, en un total de 65 milisegundos. Este ataque requiere que el atacante pueda ejecutar programas en el mismo sistema o plataforma que realiza AES.

En diciembre de 2009 se publicó un ataque a algunas implementaciones de hardware que utilizaba análisis de fallas diferenciales y permite la recuperación de una clave con una complejidad de 2 ³² . ^[32]

En noviembre de 2010, Endre Bangerter, David Gullasch y Stephan Krenn publicaron un documento que describía un enfoque práctico para una recuperación "casi en tiempo real" de claves secretas de AES-128 sin la necesidad de texto cifrado o texto sin formato. El enfoque también funciona en implementaciones de AES-128 que usan tablas de compresión, como OpenSSL. ^[33] Al igual que algunos ataques anteriores, este requiere la capacidad de ejecutar código sin privilegios en el sistema que realiza el cifrado AES, lo que puede lograrse mediante una infección de malware con mucha más facilidad que obtener la cuenta raíz. ^[34]

En marzo de 2016, Ashokkumar C., Ravi Prakash Giri y Bernard Menezes presentaron un ataque de canal lateral muy eficiente en las implementaciones de AES que pueden recuperar la clave completa de AES de 128 bits en solo 6–7 bloques de texto plano / cifrado, lo cual es una mejora sustancial sobre trabajos anteriores que requieren entre 100 y un millón de encriptaciones. ^[35] El ataque propuesto requiere privilegio de usuario estándar ya que los ataques anteriores y los algoritmos de recuperación de claves se ejecutan en menos de un minuto.

Muchas CPU modernas tienen instrucciones de hardware integradas para AES , que protegerían contra ataques de canal lateral relacionados con el tiempo. ^[36] [37]

Validación NIST / CSEC [ editar ]

El Programa de Validación del Módulo Criptográfico (CMVP) es operado conjuntamente por la División de Seguridad Informática del Instituto Nacional de Estándares y Tecnología (NIST) del Gobierno de los Estados Unidos y el Establecimiento de Seguridad de las Comunicaciones (CSE) del Gobierno de Canadá. El uso de módulos criptográficos validados para NIST FIPS 140-2es requerido por el gobierno de los Estados Unidos para el cifrado de todos los datos que tienen una clasificación de Sensible pero no clasificado (SBU) o superior. De NSTISSP # 11, Política nacional que rige la adquisición de aseguramiento de la información: "Los productos de cifrado para proteger la información clasificada serán certificados por la NSA, y los productos de cifrado destinados a proteger la información confidencial se certificarán de acuerdo con NIST FIPS 140-2". ^{[38 ]}

El Gobierno de Canadá también recomienda el uso de módulos criptográficos validados FIPS 140 en aplicaciones no clasificadas de sus departamentos.

Aunque la publicación NIST 197 (“FIPS 197”) es el documento único que cubre el algoritmo AES, los proveedores generalmente se acercan al CMVP bajo FIPS 140 y solicitan que se validen varios algoritmos (como Triple DES o SHA1 ) al mismo tiempo. Por lo tanto, es raro encontrar módulos criptográficos que estén validados exclusivamente por FIPS 197 y el propio NIST generalmente no se toma el tiempo para enumerar los módulos validados por FIPS 197 por separado en su sitio web público. En cambio, la validación FIPS 197 generalmente aparece como una notación "aprobada por FIPS: AES" (con un número de certificado FIPS 197 específico) en la lista actual de módulos criptográficos validados FIPS 140.

El Programa de Validación de Algoritmo Criptográfico (CAVP) ^[39] permite la validación independiente de la implementación correcta del algoritmo AES a un costo razonable ^{[ cita requerida ]} . La validación exitosa se muestra en la página de validaciones NIST. ^[40] Esta prueba es un requisito previo para la validación del módulo FIPS 140-2 que se describe a continuación. Sin embargo, la validación exitosa de CAVP de ninguna manera implica que el módulo criptográfico que implementa el algoritmo sea seguro. Un módulo criptográfico que carece de la validación FIPS 140-2 o la aprobación específica de la NSA no se considera seguro por el gobierno de los EE. UU. Y no se puede utilizar para proteger los datos del gobierno. ^[38]

La validación FIPS 140-2 es un desafío para lograr tanto técnica como fiscalmente. ^[41] Hay una batería estandarizada de pruebas, así como un elemento de revisión del código fuente que debe pasarse durante un período de unas pocas semanas. El costo de realizar estas pruebas a través de un laboratorio aprobado puede ser significativo (por ejemplo, más de $ 30,000 US) ^[41] y no incluye el tiempo que lleva escribir, probar, documentar y preparar un módulo para la validación. Después de la validación, los módulos deben volver a enviarse y reevaluarse si se modifican de alguna manera. Esto puede variar desde simples actualizaciones de documentación si la funcionalidad de seguridad no cambió a un conjunto más sustancial de reevaluación si la funcionalidad de seguridad se vio afectada por el cambio.

Vectores de prueba [ editar ]

Los vectores de prueba son un conjunto de cifrados conocidos para una entrada y clave dada. NIST distribuye la referencia de los vectores de prueba de AES como vectores de prueba de respuesta conocida de AES (KAT). ^{[nota 5]}

Rendimiento [ editar ]

Los requisitos de alta velocidad y baja RAM fueron criterios del proceso de selección de AES. Como algoritmo elegido, AES funcionó bien en una amplia variedad de hardware, desde tarjetas inteligentes de 8 bits hasta computadoras de alto rendimiento.

En un Pentium Pro , el cifrado AES requiere 18 ciclos de reloj por byte, ^[42] equivalente a un rendimiento de aproximadamente 11 Mbit / s para un procesador de 200 MHz. En un Pentium M de 1.7 GHz, el rendimiento es de aproximadamente 60 Mbit / s.

En las CPU Intel Core i3 / i5 / i7 y AMD Ryzen que admiten extensiones de conjunto de instrucciones AES-NI , el rendimiento puede ser de varios GB / s (incluso más de 10 GB / s).