CRIPTOGRAFÍA

Este artículo trata sobre el cifrado de bloque. Para el observatorio de axiones en Suiza, ver CERN Axion Solar Telescope .

CAST-128

General
Diseñadores	Carlisle Adams y Stafford Tavares
Publicado por primera vez	1996
Sucesores	CAST-256
Detalle de cifrado
Tamaños clave	40 a 128 bits
Tamaños de bloque	64 bits
Estructura	Red Feistel
Rondas	12 o 16

Tres rondas del cifrado de bloque CAST-128

En criptografía , CAST-128 (alternativamente CAST5 ) es un cifrado de bloque de clave simétrica utilizado en varios productos, especialmente como el cifrado predeterminado en algunas versiones de GPG y PGP . También ha sido aprobado para uso del Gobierno de Canadá por el Establecimiento de Seguridad de Comunicaciones . El algoritmo fue creado en 1996 por Carlisle Adams y Stafford Tavares utilizando el procedimiento de diseño CAST . ^[1]

Otro miembro de la familia de cifrados CAST , CAST-256 (un ex candidato de AES ) se derivó de CAST-128. Según algunas fuentes, el nombre CAST se basa en las iniciales de sus inventores, aunque Bruce Schneier informa que los autores afirman que "el nombre debería evocar imágenes de aleatoriedad". ^[2]

CAST-128 es una red Feistel de 12 o 16 rondas con un tamaño de bloque de 64 bits y un tamaño de clave de entre 40 y 128 bits (pero solo en incrementos de 8 bits). Las 16 rondas completas se utilizan cuando el tamaño de la clave es superior a 80 bits. ^[3]

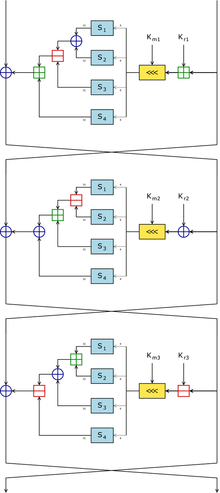
Los componentes incluyen grandes cajas S de 8 × 32 bits basadas en funciones dobladas , rotaciones dependientes de teclas, suma y resta modular , y operaciones XOR . Hay tres tipos alternos de función redonda, pero son similares en estructura y difieren solo en la elección de la operación exacta (suma, resta o XOR) en varios puntos.

Aunque Entrust posee una patente sobre el procedimiento de diseño de CAST, CAST-128 está disponible en todo el mundo sin regalías para usos comerciales y no comerciales.

En criptografía , el Algoritmo de cifrado de mensajes celulares ( CMEA ) es un cifrado de bloque que se utilizó para proteger los teléfonos móviles en los Estados Unidos . CMEA es una de las cuatro primitivas criptográficas especificadas en un estándar de la Asociación de la Industria de las Telecomunicaciones (TIA), y está diseñada para cifrar el canal de control, en lugar de los datos de voz. En 1997, un grupo de criptógrafos publicó ataques contra el cifrado que mostraban que tenía varias debilidades que le daban una fuerza trivial efectiva de un cifrado de 24 a 32 bits. ^[1] Se hicieron algunas acusaciones de que la NSAhabía presionado a los diseñadores originales para que paralizaran la CMEA, pero la NSA ha negado cualquier papel en el diseño o la selección del algoritmo. Los cifrados ECMEA y SCEMA se derivan de CMEA.

CMEA se describe en la patente de los Estados Unidos 5.159.634 . Está orientado a bytes , con un tamaño de bloque variable , típicamente de 2 a 6 bytes. El tamaño de la clave es de solo 64 bits. Ambos son inusualmente pequeños para un cifrado moderno. El algoritmo consta de solo 3 pases sobre los datos: una operación de difusión no lineal de izquierda a derecha, una mezcla lineal sin clave y otra difusión no lineal que es, de hecho, la inversa de la primera. Las operaciones no lineales usan una tabla de búsqueda con clave llamada T-box , que utiliza una tabla de búsqueda sin clave llamada CaveTable . El algoritmo es autoinverso.; volver a cifrar el texto cifrado con la misma clave es equivalente a descifrarlo.

CMEA es severamente inseguro. Hay un ataque de texto sin formato elegido , efectivo para todos los tamaños de bloque, que utiliza 338 textos sin formato seleccionados. Para los bloques de 3 bytes (generalmente utilizados para cifrar cada dígito marcado), hay un ataque de texto sin formato conocido que utiliza de 40 a 80 textos sin formato conocidos. Para bloques de 2 bytes, son suficientes 4 textos claros conocidos.

El CMEA "mejorado", CMEA-I, no es mucho mejor: el ataque de texto sin formato elegido requiere menos de 850 textos claros en su versión adaptativa.

El algoritmo Cayley-Purser fue un algoritmo de criptografía de clave pública publicado a principios de 1999 por la irlandesa Sarah Flannery , de 16 años , basado en un trabajo inédito de Michael Purser , fundador de Baltimore Technologies , una compañía de seguridad de datos de Dublín . Flannery lo nombró por el matemático Arthur Cayley . Desde entonces se ha descubierto que es defectuoso como un algoritmo de clave pública, pero fue objeto de considerable atención de los medios.

Historia [ editar ]

Durante una colocación de experiencia laboral con Baltimore Technologies, Michael Purser le mostró a Flannery un documento inédito que describía un nuevo esquema criptográfico de clave pública que utilizaba la multiplicación no conmutativa . Se le pidió que escribiera una implementación de este esquema en Mathematica .

Antes de esta colocación, Flannery había asistido a la Exposición de jóvenes científicos y tecnología de ESAT de 1998 con un proyecto que describe técnicas criptográficas ya existentes desde el cifrado César hasta RSA . Esto le había valido el Premio Intel Student, que incluía la oportunidad de competir en la Feria Internacional Intel de Ciencia e Ingeniería de 1998 en los Estados Unidos. Sintiendo que necesitaba un trabajo original para agregar a su proyecto de exhibición, Flannery le pidió permiso a Michael Purser para incluir el trabajo basado en su esquema criptográfico.

Siguiendo el consejo de su padre matemático, Flannery decidió usar matrices para implementar el esquema de Purser, ya que la multiplicación de matrices tiene la propiedad necesaria de no ser conmutativo. Como el algoritmo resultante dependería de la multiplicación, sería mucho más rápido que el algoritmo RSA que utiliza un paso exponencial . Para su proyecto de Intel Science Fair, Flannery preparó una demostración en la que se cifró el mismo texto simple utilizando RSA y su nuevo algoritmo Cayley-Purser y, de hecho, mostró una mejora significativa en el tiempo.

Volviendo a la Exposición de jóvenes científicos y tecnología de ESAT en 1999, Flannery formalizó el tiempo de ejecución de Cayley-Purser y analizó una variedad de ataques conocidos, ninguno de los cuales se determinó que era efectivo.

Flannery no hizo ninguna afirmación de que el algoritmo Cayley-Purser reemplazaría a RSA, sabiendo que cualquier nuevo sistema criptográfico necesitaría resistir la prueba del tiempo antes de que pueda ser reconocido como un sistema seguro. Sin embargo, los medios no fueron tan cautelosos y cuando recibió el primer premio en la exposición de ESAT, los periódicos de todo el mundo informaron la historia de que una joven genio había revolucionado la criptografía.

De hecho, se descubrió un ataque al algoritmo poco después, pero lo analizó y lo incluyó como un apéndice en competencias posteriores, incluida una competencia en toda Europa en la que ganó un premio importante.

Descripción general [ editar ]

La notación utilizada en esta discusión es como en el artículo original de Flannery.

Generación de claves [ editar ]

Al igual que RSA, Cayley-Purser comienza generando dos primos grandes p y q y su producto n , un semiprime . A continuación, considere GL (2, n ), el grupo lineal general de matrices 2 × 2 con elementos enteros y mod aritmética modular n . Por ejemplo, si n = 5, podríamos escribir:

{\ displaystyle \ left [{\ begin {matrix} 0 & 1 \\ 2 & 3 \ end {matrix}} \ right] + \ left [{\ begin {matrix} 1 & 2 \\ 3 & 4 \ end {matrix}} \ right] = \ left [{\ begin {matrix} 1 & 3 \\ 5 & 7 \ end {matrix}} \ right] = \ left [{\ begin {matrix} 1 & 3 \\ 0 & 2 \ end {matrix}} \ right]}

{\ displaystyle \ left [{\ begin {matrix} 0 & 1 \\ 2 & 3 \ end {matrix}} \ right] \ left [{\ begin {matrix} 1 & 2 \\ 3 & 4 \ end {matrix}} \ right] = \ left [{\ begin {matrix} 3 & 4 \\ 11 & 16 \ end {matrix}} \ right] = \ left [{\ begin {matrix} 3 & 4 \\ 1 & 1 \ end {matrix}} \ right]}

Este grupo se elige porque tiene un orden grande (para semiprime grande n ), igual a ( p ² -1) ( p ² - p ) ( q ² -1) ( q ² - q ).

Dejar $${\ displaystyle \ chi} y $${\ displaystyle \ alpha}ser dos de esas matrices de GL (2, n ) elegidas de manera que$${\ displaystyle \ chi \ alpha ^ {- 1} \ not = \ alpha \ chi}. Elija un número natural r y calcule:

$${\ displaystyle \ beta = \ chi ^ {- 1} \ alpha ^ {- 1} \ chi,}

$${\ displaystyle \ gamma = \ chi ^ {r}.}

La clave pública es $${\ displaystyle n}, $${\ displaystyle \ alpha}, $${\ displaystyle \ beta}y $${\ displaystyle \ gamma}. La clave privada es$${\ displaystyle \ chi}.

Cifrado [ editar ]

El remitente comienza generando un número natural aleatorio sy calculando:

$${\ displaystyle \ delta = \ gamma ^ {s}}

$${\ displaystyle \ epsilon = \ delta ^ {- 1} \ alpha \ delta}

$${\ displaystyle \ kappa = \ delta ^ {- 1} \ beta \ delta}

Luego, para cifrar un mensaje, cada bloque de mensajes se codifica como un número (como en RSA) y se colocan de cuatro en cuatro como elementos de una matriz de texto sin formato $${\ displaystyle \ mu}. Cada$${\ displaystyle \ mu} está encriptado usando:

$${\ displaystyle \ mu '= \ kappa \ mu \ kappa.}

Luego $${\ displaystyle \ mu '} y $${\ displaystyle \ epsilon} son enviados al receptor.

Descifrado [ editar ]

El receptor recupera la matriz de texto sin formato original. $${\ displaystyle \ mu} vía:

$${\ displaystyle \ lambda = \ chi ^ {- 1} \ epsilon \ chi,}

$${\ displaystyle \ mu = \ lambda \ mu '\ lambda.}

Seguridad [ editar ]

Recuperando la clave privada $${\ displaystyle \ chi} desde $${\ displaystyle \ gamma}es computacionalmente inviable, al menos tan difícil como encontrar mods de raíces cuadradas n (ver residuo cuadrático ). Podría ser recuperado de$${\ displaystyle \ alpha} y $${\ displaystyle \ beta} si el sistema $${\ displaystyle \ chi \ beta = \ alpha ^ {- 1} \ chi} podría resolverse, pero la cantidad de soluciones para este sistema es grande siempre que los elementos del grupo tengan un orden grande, lo que puede garantizarse para casi todos los elementos.

Sin embargo, el sistema puede romperse al encontrar un múltiple $${\ displaystyle \ chi '} de $${\ displaystyle \ chi} resolviendo para $${\ displaystyle d} en la siguiente congruencia:

$${\ displaystyle d \ left (\ beta - \ alpha ^ {- 1} \ right) \ equiv \ left (\ alpha ^ {- 1} \ gamma - \ gamma \ beta \ right) {\ pmod {n}}}

Observe que existe una solución si para algunos $${\ displaystyle i, j \ in \ left | \ gamma \ right |} y $${\ displaystyle x, y \ in \ mathbb {Z} _ {n}}

$${\ displaystyle x \ left (\ beta _ {ij} ^ {- 1} - \ alpha _ {ij} \ right) \ equiv y {\ pmod {n}}.}

Si $${\ displaystyle d} es conocida, $${\ displaystyle d \ mathrm {I} + \ gamma = \ chi '} - un múltiplo de $${\ displaystyle \ chi}. Cualquier múltiplo de$${\ displaystyle \ chi} rendimientos $${\ displaystyle \ lambda = \ kappa ^ {- 1} = v ^ {- 1} \ chi ^ {- 1} \ epsilon v \ chi}. Esto presenta una debilidad fatal para el sistema, que aún no se ha reconciliado.

Esta falla no impide el uso del algoritmo como un algoritmo mixto de clave privada / clave pública, si el remitente transmite $${\ displaystyle \ epsilon}en secreto, pero este enfoque no presenta ninguna ventaja sobre el enfoque común de transmitir una clave de cifrado simétrico utilizando un esquema de cifrado de clave pública y luego cambiar al cifrado simétrico, que es más rápido que Cayley-Purser.