Geometría diferencial

 conexión es un objeto matemático definido en una variedad diferenciable que permite establecer una relación o "conectar" la geometría local en torno a un punto con la geometría local en torno a otro punto. El caso más sencillo de conexión es una conexión afín que permite especificar una derivada covariante en una variedad diferenciable.La teoría de conexiones conduce a los invariantes de curvatura (véase también tensor de curvatura), y la torsión. Esto se aplica a los fibrados tangentes; hay conexiones más generales, en geometría diferencial: una conexión puede referirse a una conexión en cualquier fibrado vectorial o a una conexión en un fibrado principal.

En un acercamiento particular, una conexión es una 1-forma a valores en un álgebra de Lie que es un múltiplo de la diferencia entre la derivada covariante y la derivada parcial ordinaria. Es decir, la derivada parcial no es una noción intrínseca en una variedad diferenciable: una conexión corrige el concepto y permite la discusión en términos geométricos. Las conexiones dan lugar a un transporte paralelo.Hay un gran número de enfoques posibles relacionados con el concepto de conexión, entre los cuales están los siguientes:

• Un muy directo estilo módulo a la diferenciación covariante, indicando las condiciones que permiten a los campos vectoriales a actuar sobre secciones de fibrados vectoriales.
• La notación tradicional de índices especifica la conexión por los componentes, vea derivada covariante (tres índices, pero esto no esun tensor).
• En geometría de Riemann hay una manera de derivar una conexión del tensor métrico (conexión de Levi-Civita).
• Usando fibrados principales y formas diferenciales a valores en un álgebra de Lie (véase conexión de Cartan).
• el acercamiento más abstracto puede ser el sugerido por Alexander Grothendieck, donde se considera una conexión como descensode vecindades infinitesimales de la diagonal.

Las conexiones referidas arriba son conexiones lineales o afines. Hay también un concepto de conexión proyectiva; la forma más comúnmente de esto es derivado de Schwarz en análisis complejo.

El transporte paralelo de un vector a lo largo de una curva cerrada sobre la esfera, que al igual que el concepto de derivada covariante se basa en la noción de conexión matemática. El ángulo  después de recorrer una vez la curva es proporcional al área dentro de la curva.

 conexión de Cartan en geometría diferencial es una generalización amplia del concepto de la conexión, basado en una comprensión del papel del grupo afín en el acercamiento usual. Fue desarrollado por Élie Cartan, como parte (y como manera de formular) su método de triedro móvil. Véase también formalismo de Cartan- ....................................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=6d995bc751e4443c2ac2b824babe458700a82866&writer=rdf2latex&return_to=Conexi%C3%B3n+de+Cartan

  

 conexión lineal puede referirse a cualquiera de los siguientes conceptos:

• una conexión o bulto vectorial, frecuentemente visto como un operador diferencial (una conexión de Koszul o derivada covariante);
• una conexión principal sobre el marco del bulto de una variedad o la conexión inducida sobre cualquier bulto asociado — tal conexión es equivalente a una dada por la conexión de Cartan para el grupo afín de un espacio afín, y se llama una conexión afín.

Los dos significados son válidos en la noción de una conexión lineal sobre el fibrado tangente de una variedad.

En la literatura antigua, el término conexión lineal es ocasionalmente usada para una conexión de Ehresmann o conexión de Cartansobre un bulto fibrado arbitrario,¹ para enfatizar que estas conexiones son lineales en la dirección tangente (es decir, el bulto horizontal es un vector del subbulto del bulto tangente de un bulto fibrado), siempre que no sean lineales en la dirección fibrada.

conjunto rectificable es un conjunto que intuitivamente puede ser aproximado en el entorno de cada punto por un espacio euclídeo.

Muchos objetos matemáticos definidos mediante aplicaciones diferenciables son rectificables (también llamados suaves). Mientras que muchos objetos fractales de aspecto irregular no suelen ser rectificables.Un conjunto de  es rectificable si en casi en todas partes de su frontera topológica admite un espacio tangente.

Un subconjunto de  es rectificable si dicho conjunto puede ser recubierto casi en todas partes por una colección numerable de piezas de Lipschitz  tales que:

donde:

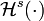 es la medida de Hausdorff.

• Una circunferencia es un ejemplo de curva continua, cerrada y diferenciable que además es rectificable.
• La frontera de un polígono cerrado es un ejemplo de curva continua, cerrada aunque no diferenciable en los vértices que aun así es rectificable, y por tanto dado un polígono de n lados su perímetro tiene una longitud finita.
• La curva de Koch es una curva no rectificable, su longitud no es finita, sin embargo encierra un área finita.