curvatura se refiere a cualquiera de una serie de conceptos vagamente relacionados en las diferentes áreas de lageometría. Normalmente se refiere a un concepto métrico de objetos matemáticos o geométricos. Por extensión también se usa el término para referirse a un número u objeto matemático que caracteriza la forma y magnitud de la curvatura. Más específicamente el término curvatura puede referirse a alguno de estos conceptos:
- Geometría diferencial de curvas:
- Geometría diferencial general:
- Física:
Curvatura de Gauss
La curvatura gaussiana de una superficie es un número real  (P0) que mide la curvatura intrínseca en cada punto regular P0 de una superficie. Esta curvatura puede calcularse a partir de los determinantes de la primera y segunda formas fundamentales de la superficie:
(P0) que mide la curvatura intrínseca en cada punto regular P0 de una superficie. Esta curvatura puede calcularse a partir de los determinantes de la primera y segunda formas fundamentales de la superficie:
 (P0) que mide la curvatura intrínseca en cada punto regular P0 de una superficie. Esta curvatura puede calcularse a partir de los determinantes de la primera y segunda formas fundamentales de la superficie:
(P0) que mide la curvatura intrínseca en cada punto regular P0 de una superficie. Esta curvatura puede calcularse a partir de los determinantes de la primera y segunda formas fundamentales de la superficie:
Esta curvatura gaussiana en general varía de un punto a otro de la superficie y está relacionada con las curvaturas principales de cada punto (k1 y k2), mediante la relación K = k1k2.
Un caso interesante de superficie es la esfera, que tiene la misma curvatura en todos sus puntos. Calculando la curvatura de Gauss de una esfera (2-esfera). A partir de la fórmula anterior se llega fácilmente a que para una esfera de radio r, la curvatura gaussiana es igual en todos los puntos e igual a 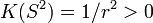 .
.
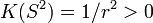 .
.
Si bien observamos que hay superficies que tienen curvatura constante, la curvatura gaussiana debe verse como una relación  donde
donde  (una función diferenciable sobre S) que asigna a cada superficie su función de curvatura gaussiana.
(una función diferenciable sobre S) que asigna a cada superficie su función de curvatura gaussiana.
La manera actual de definir la curvatura gaussiana es mediante el operador de forma (del inglés shape operator) de la superficie S:
 donde
donde  (una función diferenciable sobre S) que asigna a cada superficie su función de curvatura gaussiana.
(una función diferenciable sobre S) que asigna a cada superficie su función de curvatura gaussiana.La manera actual de definir la curvatura gaussiana es mediante el operador de forma (del inglés shape operator) de la superficie S:
-
 , definido mediante
, definido mediante 
Donde
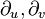 son los vectores tangentes coordenados y están siendo evaluados en la posición p.
son los vectores tangentes coordenados y están siendo evaluados en la posición p.
Con la derivada (jacobiano) del operador de forma
uno obtiene una transformación lineal auto-adjunta -llamada transformación de Weingarten- y así, la curvatura gaussiana es determinante de L, i.e.
Es relativamente fácil verificar que coincide con la definición dada arriba.
En términos de los componentes del tensor de curvatura de Riemann para las 2-variedad diferenciables, uno encuentra la relación
Ejemplo, la curvatura gaussiana de un toro es 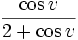 donde se ha usado la parametrización:
donde se ha usado la parametrización:
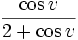 donde se ha usado la parametrización:
donde se ha usado la parametrización:
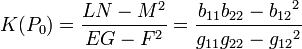
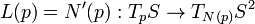
![K(p)=\det[L(p)]\,](https://upload.wikimedia.org/math/5/b/4/5b404ee862596fee340f5d38912793af.png)


No hay comentarios:
Publicar un comentario