curvatura media  de una superficie
de una superficie  es una medida extrínseca de curvatura definida en geometría diferencial y que localmente describe la curvatura de una superficie inmersa surface en algunos ambientes como el espacio euclídeo.
es una medida extrínseca de curvatura definida en geometría diferencial y que localmente describe la curvatura de una superficie inmersa surface en algunos ambientes como el espacio euclídeo.
 de una superficie
de una superficie  es una medida extrínseca de curvatura definida en geometría diferencial y que localmente describe la curvatura de una superficie inmersa surface en algunos ambientes como el espacio euclídeo.
es una medida extrínseca de curvatura definida en geometría diferencial y que localmente describe la curvatura de una superficie inmersa surface en algunos ambientes como el espacio euclídeo.
El concepto fue introducido por Sophie Germain en su trabajo sobre teoría de la elasticidad.Sea  un punto sobre la superficie
un punto sobre la superficie  . Considerense todas las curvas
. Considerense todas las curvas  sobre
sobre  que pasan a través del punto
que pasan a través del punto  sobre la superficie. Tales
sobre la superficie. Tales  tienen una curvatura asociada
tienen una curvatura asociada 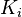 dada en
dada en  . De todas esas curvaturas
. De todas esas curvaturas 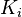 , al menos una está caracterizada como máxima,
, al menos una está caracterizada como máxima, 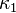 y otra como mínima,
y otra como mínima,  , y esas dos curvaturas
, y esas dos curvaturas  son conocidas como las curvaturas principales de
son conocidas como las curvaturas principales de  .
.
 un punto sobre la superficie
un punto sobre la superficie  . Considerense todas las curvas
. Considerense todas las curvas  sobre
sobre  que pasan a través del punto
que pasan a través del punto  sobre la superficie. Tales
sobre la superficie. Tales  tienen una curvatura asociada
tienen una curvatura asociada 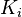 dada en
dada en  . De todas esas curvaturas
. De todas esas curvaturas 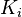 , al menos una está caracterizada como máxima,
, al menos una está caracterizada como máxima, 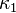 y otra como mínima,
y otra como mínima,  , y esas dos curvaturas
, y esas dos curvaturas  son conocidas como las curvaturas principales de
son conocidas como las curvaturas principales de  .
.
La curvatura media en 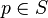 es la media de las curvaturas (Spivak, 1999, Volumen 3, Capítulo 2), y de ahí su nombre:
es la media de las curvaturas (Spivak, 1999, Volumen 3, Capítulo 2), y de ahí su nombre:
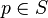 es la media de las curvaturas (Spivak, 1999, Volumen 3, Capítulo 2), y de ahí su nombre:
es la media de las curvaturas (Spivak, 1999, Volumen 3, Capítulo 2), y de ahí su nombre: put
put
Más generalmente (Spivak, 1999, Volumen 4, Capítulo 7), para una hipersuperficie  la curvatura media está dada por
la curvatura media está dada por
 la curvatura media está dada por
la curvatura media está dada por
- derivación, matemáticamente, es un concepto esencial para determinar los espacios tangentes sobre variedades diferenciables, sus cualidades, sus propiedades y sus consecuencias.Es una pieza fundamental, clave en el desarrollo de la teoría para la geometría diferencial tal y como está estructurada actualmente.- ....................................:https://es.wikipedia.org/w/index.php?title=Derivaci%C3%B3n_(matem%C3%A1tica)&printable=yes
- derivada covariante (
 ) es una generalización del concepto de derivada parcial (
) es una generalización del concepto de derivada parcial ( ) que permite extender el cálculo diferencial sobre
) que permite extender el cálculo diferencial sobre 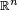 con coordenadas cartesianas al caso decoordenadas curvilíneas en
con coordenadas cartesianas al caso decoordenadas curvilíneas en 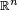 (y también al caso todavía más general de variedades diferenciables).- ........................................:https://es.wikipedia.org/w/index.php?title=Derivada_covariante&printable=yes
(y también al caso todavía más general de variedades diferenciables).- ........................................:https://es.wikipedia.org/w/index.php?title=Derivada_covariante&printable=yes - derivada de Lie es una derivación en el álgebra de funciones diferenciables sobre una variedad diferenciable
 , cuya definición puede extenderse al álgebra tensorial de la variedad. Obtenemos entonces lo que en topología diferencial se denomina derivación tensorial: una aplicación
, cuya definición puede extenderse al álgebra tensorial de la variedad. Obtenemos entonces lo que en topología diferencial se denomina derivación tensorial: una aplicación 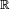 -lineal sobre el conjunto de tensores de tipo (r,s), que preserva el tipo tensorial y satisface la regla del producto de Leibniz y que conmuta con las contracciones.Para definir la derivada de Lie sobre el conjunto de tensores de tipo (r,s) bastará con definir su acción sobre funciones y sobre campos de vectores: Así, si X es un campo diferenciable de vectores, se define la derivada de Lie con respecto a X como la única derivación tensorial tal que:1
-lineal sobre el conjunto de tensores de tipo (r,s), que preserva el tipo tensorial y satisface la regla del producto de Leibniz y que conmuta con las contracciones.Para definir la derivada de Lie sobre el conjunto de tensores de tipo (r,s) bastará con definir su acción sobre funciones y sobre campos de vectores: Así, si X es un campo diferenciable de vectores, se define la derivada de Lie con respecto a X como la única derivación tensorial tal que:1 para toda función diferenciable f.
para toda función diferenciable f.![\mathcal L_XY = [X, Y].](https://upload.wikimedia.org/math/2/c/0/2c0f8ba2e7d5bf36342dbe965cc9ad60.png) para todo campo diferenciable Y. Donde [,] es el corchete de Lie.
para todo campo diferenciable Y. Donde [,] es el corchete de Lie.
La derivada así definida satisfará automáticamente las propiedades citadas de una derivación tensorial:- la regla del producto
- conmutará con las contracciones.
El espacio vectorial de todas las derivadas de Lie en M forma a su vez un álgebra de Lie infinito dimensional con respecto al corchete de Lie. - En geometría diferencial, si tenemos un tensor diferenciable T de rango (p, q) (es decir una función lineal de secciones diferenciables, α, β, ... del T*M fibrado cotangente y X, Y,... del TM fibrado tangente,T(α,β...,X,Y ,...)Tales que para cualesquiera funciones diferenciablesf1...,fp...,fp+q, T(f1α,f2β...,fp+1X,fp+2Y,...) = f1f2... fp+1fp+2... fp+q T(α, β..., X, Y ,...)) y un campo vectorial (sección del fibrado tangente) Adiferenciable, entonces la función lineal:(£AT)(α, β,..., X, Y,...) ≡ ∇A T(α, β,..., X, Y,...) - ∇T(-,β...,X,Y,...)A(α)-... + T(α, β...,∇XA,Y,...)+...es independiente de la conexión ∇ que se utiliza, mientras sea libre de torsión, y es, de hecho, un tensor.2Este tensor se llama la derivada de Lie de T con respecto a A.
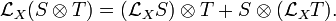
No hay comentarios:
Publicar un comentario