Geometría diferencial

derivada direccional de una función multivariable sobre un vector dado, representa la tasa de cambio de la función en la dirección de dicho vector. Este concepto generaliza a las derivadas parciales, ya que estas son derivadas direccionales en los vectores paralelos a los ejes.- ...........................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=8584d135438b10ebdf702d3661697740ee4a3bfe&writer=rdf2latex&return_to=Derivada+direccional

 






derivada exterior (o diferencial exterior) de la topología diferencial, amplía el concepto del diferencialde una función a formas diferenciales de un grado más alto. Fue inventado, en su forma actual, por Élie Cartan.La derivada exterior de una forma diferencial de grado k es una forma diferencial de grado k+1. La diferenciación exterior satisface tres propiedades importantes:

• dƒ es el diferencial de ƒ para cualquier 0-forma ƒ (funciones de la clase C^∞).

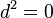• , dicho de otro modo, que siempre: , para cualquier forma .

• La regla del producto cuña:

.

Puede ser demostrado que la derivada exterior está determinada unívocamente por estas propiedades y su coincidencia con el diferencial en 0-formas (funciones).

Los casos especiales de la diferenciación exterior corresponden a los operadores diferenciales familiares del cálculo vectorial a lo largo de las mismas líneas que el diferencial corresponde a gradiente. Por ejemplo, en el espacio euclidiano tridimensional, la derivada exterior de una 1-forma corresponde al rotacional y la derivada exterior de 2-formas corresponde a la divergencia. Esta correspondencia muestra más de una docena de fórmulas del cálculo vectorial como casos especiales de las tres reglas antedichas de la diferenciación exterior. Elnúcleo del operador  consiste en las formas cerradas, y la imagen en las formas exactas (cf. diferenciales exactos).

Notación y Preliminares.

Dejar M ser una ndimensional variedad diferencial . DejarTMdenotar el colector 'stangente paquete ,C∞( M)el álgebra de funciones suaves , yV( M)el álgebra de Liede suaves campos vectoriales . Los derivados direccionales marcasC∞( M) en un V( M) módulo . Usando coordenadas locales , la derivada direccional operación se puede expresar como

v( f) = vyo∂yoF, v ∈ V( M) , f∈ C∞( M) .

2 Definiciones.

Formas diferenciales.

Dejar LA ser una C∞( M)módulo. UnR- aplicación lineal α : V( M) → Ase dice que es tensorial si es una C∞( M)- homomorfismo , en otras palabras , si es que satisface

α( fv ) = fα( v )

para todos para todos los campos vectoriales v ∈ V( M)y funciones F∈ C∞( M).Más generalmente, un multilineal mapa α : V( M) × ... × V( M) → A se llama tensorial si satisface

α( fu , ... , v ) = ⋯ = α( u , ... , fv ) = fα( u , ... , v )

para todos los campos vectoriales u , ... , v y todas las funciones F∈ C∞( M).

Definimos ahora un diferencial de 1-forma de ser una aplicación lineal tensorial deV( M) a C∞( M). Más en general, parak = 0 , 1 , 2 , ... , definimos un diferencial k-forma para ser un multilineal tensorial, antisimétrica , mapeo deV( M) × ⋯ × V( M) (k veces) para C∞( M). Usando un poco más elegantelenguaje , las cantidades anteriores a decir que una1-form es una sección del fibrado cotangente T*M= Hom( TM, R ), Mientras que un diferencial k-Forma como una sección de Hom( ΛkTM, R ).

De ahora en adelante, dejamos Ωk( M) denotar la C∞( M)-module de diferencial k-formas. En particular, un diferencial0-forma es lo mismo que una función. Dado que los espacios tangentes deM son n-dimensionales espacios vectoriales , también tenemosΩk( M) = 0 para k > n. Dejamos

Ω( M) = ⊕k = 0nΩk( M)

denotar el espacio vectorial de todas las formas diferenciales . Hay un natural deoperador , llamado el producto exterior , que dotaΩ( M)con la estructura de unálgebra graduada . Se describe esta operación más adelante.

Exterior e interior del producto.

Dejar v ∈ V( M) ser un campo de vector y alpha ∈ omegak( M)una forma diferencial.Definimosιv( ω ), El producto interior dev y α, Para ser el diferencial k - 1 forma dada por

ιv( α )( u1, ... , uk - 1) = α( v , v1, ... , vk - 1) , v1, ... , vk - 1∈ V( M) .

El producto interior de un campo vectorial con un 0-forma se define como cero .

Dejar alpha ∈ omegak( M) y β∈ omegaℓ( M)ser formas diferenciales. Definimos el exterior , oproducto exterior alpha ∧ beta∈ omegak + ℓ( M) ser la única forma diferencial tal que

ιv( alpha ∧ beta) = ιv( α ) ∧ beta+ ( - 1 )kalpha ∧ Év( β)

para todos los campos vectoriales v ∈ V( M). De manera equivalente, podríamos haber definido

( alpha ∧ beta)( v1, ... , vk + ℓ) = Σπsgn( π)α( vπ1, ... , vπk)β( vπk + 1, ... , vπk + ℓ) ,

donde la suma se toma sobre todas las permutaciones π de { 1 , 2 , ... , k + ℓ } de tal manera que π1< π2< ⋯πk y πk + 1< ⋯ < πk + ℓ, y donde sgnπ= ± 1 en función de si πes una incluso o permutación impar .

Derivado del exterior.

La derivada exterior es una de primer orden operador diferencial d: Ω*( M) → omega*( M), Que se puede definir como la aplicación lineal única que satisface

	d( dα )	= 0 , alpha ∈ omegak( M) ;
	ιV( dF)	= v ( f) , v ∈ V( M) , f∈ C∞( M) ;
	d( alpha ∧ beta)	= d( α ) ∧ beta+ ( - 1 )kalpha ∧ d( β) , alpha ∈ omegak( M) , β∈ omegaℓ( M) .

3 coordenadas locales.

Dejar ( x1, ... , xn) ser un sistema de coordenadas locales en M, y deja ∂1, ... , ∂ndenotar el correspondiente marco de coordenadas vectoriales campos . En otras palabras,

∂yo( xj) = δyo,j

donde el lado derecho es el habitual delta Kronecker símbolo. Por la definición de la derivada exterior,

ι∂yo( dXj) = δyo;j

En otras palabras, el 1-formas dX1, ... , dXnformar la doble coframe .

A nivel local, la ∂yo libremente generar V( M), Lo que significa que cada campo vectorial v ∈ V( M) tiene la forma

v = vyo∂yo,

donde la coordenada componentes vyo se determinan de forma única como

vyo= v( xyo) .

Del mismo modo, el localmente dXyo libremente generar Ω1( M). Esto significa que cada uno en forma dealpha ∈ omega1( M) toma la forma

α = αyodXyo,

dónde

αyo= ι∂yo( α ) .

Más en general, localmente Ωk( M)es un libre generado por el diferencialk-formas

dXyo1∧ ⋯ ∧ dXyok, 1 ≤ i1< i2< ⋯ < ik≤ n .

Por lo tanto, una forma diferencial alpha ∈ omegak( M) es dado por

	α	= Σyo1< ... < ikαyo1...yokdXyo1∧ ... ∧ dXyok,		(1)
		= 1k !αyo1...yokdXyo1∧ ... ∧ dXyok,

dónde

αyo1...yok= α( ∂yo1, ... , ∂yok) .

En consecuencia, para los campos de vectores u , v , ... , w ∈ V( M), tenemos

α( u , v , ... , w ) = αyo1yo2...yokuyo1vyo2⋯wyok.

En términos de coordenadas locales y el hemi-simetrización índice de notación, elinterior y el exterior del producto, y la derivada exterior tome las siguientesexpresiones :

	( ιv( α ) )yo1...yok	= vjαjyo1...yok, v ∈ V( M) , alpha ∈ omegak + 1( M) ;		(2)
	( alpha ∧ beta)yo1...yok + ℓ	= ( k + ℓk) α[ i1... ikβyok + 1... ik + ℓ], alpha ∈ omegak( M) , β∈ omegaℓ( M) ;		(3)
	( dα )yo0yo1...yok	= ( k + 1 ) ∂[ i0αyo1... ik], alpha ∈ omegak( M) .		(4)

Tenga en cuenta que algunos autores prefieren una definición diferente de los componentes de un diferencial. De acuerdo con este convenio alternativo, un factor dedek !colocan antes de la sumatoria signo de ( 1 ), y de los factores principales se eliminan de ( 3 ) y ( 4 ).

Diferenchttps://es.wikipedia.org/w/index.php?title=Diferencial_(matem%C3%A1tica)&printable=yesial (matemática).- .........................................................:https://es.wikipedia.org/w/index.php?title=Diferencial_(matem%C3%A1tica)&printable=yes