Grupos de Lie
función especial es una función matemática particular, que por su importancia en el campo del análisis matemático, análisis funcional, la física y otras aplicaciones, posee nombres y designaciones más o menos establecidos.
No existe una definición general de las mismas, pero la lista de funciones matemáticas contiene funciones que son generalmente aceptadas como especiales. En particular, las funciones elementales son también consideradas funciones especiales.Muchas funciones especiales se originan como soluciones a ecuaciones diferenciales o integrales de funciones elementales. Por lo tanto, las tablas de integrales 1 por lo general incluyen la descripción de algunas funciones especiales, y las tablas de funciones especiales 2 incluyen las integrales más importantes; por lo menos, la representación integral de las funciones especiales.
Lenguajes computacionales de cálculo analítico tales como Mathematica3 por lo general reconocen a la mayoría de las funciones especiales. Sin embargo, no todos los sistemas de cálculo poseen algoritmos eficientes de evaluación, especialmente en el plano complejo.En la mayoría de los casos, se utiliza la siguiente notación estándar para indicar una función especial: el nombre de la función (escrita enletra Roman), subíndices, si es que tiene, se abre paréntesis, y luego sus variables independientes, separados por comas. Esta notación permite traducir las expresiones a lenguajes algorítmicos sin ambigüedades. Algunas funciones con nomenclaturas reconocidas internacionalmente son sin, cos, exp, erf, erfc, ln.
A veces, una función especial puede tener varios nombres. El logaritmo natural puede ser llamado Log, log o ln, según cual sea el contexto. La tangente puede ser llamada Tan, tan o tg (especialmente en la literatura rusa); arctangent puede ser llamado atan, arctg, ang tan, . La función de Bessel puede ser llamada
. La función de Bessel puede ser llamada  ; y por lo general,
; y por lo general,  ,
, 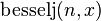 ,
, ![~ {\rm BesselJ}[n,x]~](https://upload.wikimedia.org/math/5/4/d/54dd1f04507b14ca7af143b62fdf3d19.png) hace referencia a la misma función.
hace referencia a la misma función.
 . La función de Bessel puede ser llamada
. La función de Bessel puede ser llamada  ; y por lo general,
; y por lo general,  ,
, 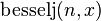 ,
, ![~ {\rm BesselJ}[n,x]~](https://upload.wikimedia.org/math/5/4/d/54dd1f04507b14ca7af143b62fdf3d19.png) hace referencia a la misma función.
hace referencia a la misma función.
A menudo los subíndices se utilizan para indicar argumentos, que se supone es un número entero. En algunos casos, el punto y coma (;) o aún la barra invertida (\) son usados como separadores. Esto hace más compleja la traducción a lenguajes algorítmicos y puede prestarse a confusiones.
Un superíndice puede no solo indicar un exponencial, sino una modificación de la función. Por ejemplo,  ,
,  ,
, 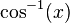 puede hacer referencia a
puede hacer referencia a  ,
,  ,
,  (o
(o  ), respectivamente; pero
), respectivamente; pero 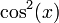 casi nunca significa
casi nunca significa  .
.
 ,
,  ,
, 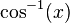 puede hacer referencia a
puede hacer referencia a  ,
,  ,
,  (o
(o  ), respectivamente; pero
), respectivamente; pero 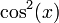 casi nunca significa
casi nunca significa  .
.
El logaritmo natural se lo puede escribir como Log(x), log(x) o ln(x), según el contexto.
función elíptica es, hablando toscamente, una función definida sobre el plano complejo y periódica en ambas direcciones. Las funciones elípticas pueden ser vistas como generalizaciones de las funciones trigonométricas (las cuales únicamente tienen la periodicidad en una dirección, paralela a la recta real). Históricamente, las funciones elípticas fueron descubiertas como las funciones inversas de las integrales elípticas; estas fueron estudiadas en relación con el problema de la longitud de arco en una elipse, de donde el nombre se deriva.Formalmente, una función elíptica es una función meromorfa f definida sobre C para la que existen dos números complejos no nulos a yb tal que
- f(z + a) = f(z + b) = f(z) para todo z perteneciente a C
y tal que a/b no es un real. De esto se deduce que
- f(z + ma + nb) = f(z) para todo z perteneciente a C y para todo entero m y n.
En el desarrollo de la teoría de las funciones elípticas, la mayoría de autores modernos utilizan la notación creada por Karl Weierstrass: la notación de las funciones elípticas en forma de Weierstrass basadas en la función  es cómoda y cualquier función elíptica puede ser expresada a partir de estas. Weierstrass se interesó en estas funciones cuando era estudiante de Christoph Gudermann, un estudiante de Carl Friedrich Gauss. Las funciones elípticas introducidas por Carl Jacobi, y la función auxiliar theta (no doble periódica), son más complicadas pero ambas importantes para la historia y para la teoría general. La diferencia más importante entre estas dos teorías es que las funciones de Weierstrass tienen polos de alto orden situados en las esquinas de un retículo periódico, mientras que las funciones de Jacobi tienen polos simples.
es cómoda y cualquier función elíptica puede ser expresada a partir de estas. Weierstrass se interesó en estas funciones cuando era estudiante de Christoph Gudermann, un estudiante de Carl Friedrich Gauss. Las funciones elípticas introducidas por Carl Jacobi, y la función auxiliar theta (no doble periódica), son más complicadas pero ambas importantes para la historia y para la teoría general. La diferencia más importante entre estas dos teorías es que las funciones de Weierstrass tienen polos de alto orden situados en las esquinas de un retículo periódico, mientras que las funciones de Jacobi tienen polos simples.
 es cómoda y cualquier función elíptica puede ser expresada a partir de estas. Weierstrass se interesó en estas funciones cuando era estudiante de Christoph Gudermann, un estudiante de Carl Friedrich Gauss. Las funciones elípticas introducidas por Carl Jacobi, y la función auxiliar theta (no doble periódica), son más complicadas pero ambas importantes para la historia y para la teoría general. La diferencia más importante entre estas dos teorías es que las funciones de Weierstrass tienen polos de alto orden situados en las esquinas de un retículo periódico, mientras que las funciones de Jacobi tienen polos simples.
es cómoda y cualquier función elíptica puede ser expresada a partir de estas. Weierstrass se interesó en estas funciones cuando era estudiante de Christoph Gudermann, un estudiante de Carl Friedrich Gauss. Las funciones elípticas introducidas por Carl Jacobi, y la función auxiliar theta (no doble periódica), son más complicadas pero ambas importantes para la historia y para la teoría general. La diferencia más importante entre estas dos teorías es que las funciones de Weierstrass tienen polos de alto orden situados en las esquinas de un retículo periódico, mientras que las funciones de Jacobi tienen polos simples.
El estudio de las funciones elípticas está estrechamente relacionado con el estudio de las funciones modulares y las formas modulares, relación demostrada por el teorema de Taniyama-Shimura. Algunos ejemplos de esta relación son el invariante j, las series de Eisensteiny la función eta de Dedekind.Cualquier número ω tal que f(z + ω) = f(z) para toda z de C se le llama period de f. Si dos periodos a y b son tales que cualquier otro periodo ω puede ser escrito como ω = ma + nb con m y n enteros , entonces a y b se les llama periodos fundamentales. Toda función elíptica tiene un par fundamental de períodos, aunque este par no es único, como se describe más adelante.
Si a y b son periodos fundamentales que describen un retículo, entonces exactamente el mismo retículo puede ser obtenido por los periodos fundamentales a' y b' donde a' = p a + q b y b' = r a + s b donde p, q, r y s son enteros que satisfacen p s − q r = 1. Dicho de otra forma, la matriz  tiene determinante unidad, por lo que pertenece al grupo modular. En otras palabras, si a y b son periodos fundamentales de una función elíptica, entonces también lo son a' y b' .
tiene determinante unidad, por lo que pertenece al grupo modular. En otras palabras, si a y b son periodos fundamentales de una función elíptica, entonces también lo son a' y b' .
 tiene determinante unidad, por lo que pertenece al grupo modular. En otras palabras, si a y b son periodos fundamentales de una función elíptica, entonces también lo son a' y b' .
tiene determinante unidad, por lo que pertenece al grupo modular. En otras palabras, si a y b son periodos fundamentales de una función elíptica, entonces también lo son a' y b' .
Si a y b son periodos fundamentales, entonces cualquier paralelogramo con vertices z, z + a, z + b, z + a + b se le llama paralelogramo fundamental. Moviendo dicho paralelogramo múltiples de a y b obtenemos una copia del paralelogramo, y la función f se comporta idénticamente sobre todas esas copias, debido a esta periodicidad.
El número de polos es cualquier paralelogramo es finito (e igualmente para todo paralelogramo fundamental). A no ser que la función elíptica sea constante, todo paralelogramo fundamental tiene al menos un polo como consecuencia del teorema de Liouville.
La suma de los órdenes de los polos en cualquier paralelogramo fundamental se le llama el orden de la función elíptica. La suma de losresiduos de los polos en cualquier paralelogramos fundamental es igual a cero, en particular, ninguna función elíptica puede tener orden uno.
El número de ceros (contados con su multiplicidad) en cualquier paralelogramo fundamental es igual al orden de la función elíptica.
La derivada de una función elíptica es otra función elíptica con los mismos periodos. El conjunto de todas las funciones elípticas con el mismo periodo fundamental forman un cuerpo.
Las funciones elípticas en forma de Weierstrass  son el prototipo de función elíptica, y de hecho, el cuerpo de funciones elípticas para un retículo dado se genera a partir de
son el prototipo de función elíptica, y de hecho, el cuerpo de funciones elípticas para un retículo dado se genera a partir de  y su derivada
y su derivada  .
.
 son el prototipo de función elíptica, y de hecho, el cuerpo de funciones elípticas para un retículo dado se genera a partir de
son el prototipo de función elíptica, y de hecho, el cuerpo de funciones elípticas para un retículo dado se genera a partir de  y su derivada
y su derivada  .
.Funciones elípticas de Jacobi
En esta página se estudia las oscilaciones de una partícula bajo la acción de dos muelles elásticos, como aplicación de las funciones elípticas de Jacobi sn u, cn u, dn u que se definen del siguiente modo:
Representamos la función elíptica de Jacobi sn(x) para dos valores de k2: 0.1 y 0.9
x=linspace(0,10,200);
[sn,cn,dn]=ellipj(x,0.1);
hold on
plot(x,sn,'b')
[sn,cn,dn]=ellipj(x,0.9);
plot(x,sn,'r')
hold off
ylim([-1.05,1.05])
xlabel('x')
ylabel('sn(x)')
legend ('0.1','0.9')
title('Funciones elípticas de Jacobi')
grid on
El péndulo
El principio de conservación de la energía establece que la suma de la energía cinética de rotación del péndulo más la potencial es constante. La energía potencial del centro de masa del sólido rígido vale
mgh=mgb(1-cosθ ).
b es la distancia entre el centro de masa (c.m.) y el eje de rotación O del sólido rígido
Cuando el péndulo alcanza la máxima desviación ω=0, y E=mgb(1-cosθ0)
Despejando el tiempo dt en la ecuación diferencial
Sustituyendo
resulta
Integramos
Despejamos la posición angular θ en función del tiempo t del siguiente modo
Representamos en color azul la posición angular θ en función del tiempo t/P0 y la comparamos con la aproximación de las oscilaciones de pequeña amplitud θ=θ0·sin(2π·t/P0) en color rojo. La amplitud es θ0=π/6 (30°).
ang=pi/6; %30°
k=sin(ang/2);
t=0:0.01:3;
x=2*asin(k*ellipj(2*pi*t,k));
xx=ang*sin(2*pi*t);
plot(t,x,'b',t,xx,'r');
xlabel('t/P_0')
ylabel('\theta')
title('Posición angular en función del tiempo')
grid on
Oscilador
Sea un bloque de masa m unido a dos muelles elásticos iguales de constante k. La longitud de los muelles si deformar es l0, cuando el sistema está en la posición de equilibrio estable x=0.
Cuando se separa el bloque una distancia x de la posición de equilibrio y se suelta, empieza a oscilar con un periodoP.
|
Ecuación del movimiento
La fuerza F que ejerce cada uno de los muelles sobre el bloque es
La resultante es
La ecuación del movimiento es
Esta ecuación, se resuelve aplicando procedimientos numéricos con las condiciones iniciales siguientes: en el instante inicial t=0, x=A, y v=dx/dt=0, siendo A la amplitud de la oscilación.
Solución analítica
La ecuación del movimiento se escribe
Cuando x<<l0 la ecuación diferencial se aproxima a
Las condiciones iniciales son: en el instante t=0, la partícula parte de la posición x=A, con velocidad nula,v=dx/dt=0
Integramos esta ecuación diferencial
es el módulo de la velocidad
Como la partícula parte de x=+A y se dirige hacia el origen la velocidad es negativa en el primer cuarto de periodo
Para obtener la posición x del oscilador en función del tiempo t tenemos que integrar nuevamente
Hacemos el cambio de variable
La integral se transforma
Se hace el cambio de variable z=sinφ
Las funciones sn y cn están relacionadas
sn2 u+cn2 u=1
Deshacemos el cambio de variable de z a x.
Tomando l0=1, k/m=60, representamos el desplazamiento x del oscilador en función del tiempo t, para dos valores de la amplitud A=0.15 y A=0.3
k_m=sqrt(60);
A=0.15;
t=0:0.2:25;
[sn,cn,dn]=ellipj(A*k_m*t,1/2);
hold on
plot(t,cn*A,'b')
A=0.3;
[sn,cn,dn]=ellipj(A*k_m*t, 1/2);
plot(t,cn*A,'r')
hold off
xlabel('t')
ylabel('x')
legend ('0.15','0.3')
title('Desplazamiento en función del tiempo')
grid on
Periodo del movimiento
El tiempo que tarda en describir un cuarto de periodo P es
Haciendo el cambio de variable x=Acosφ
El último término es la integral elíptica completa de primera especie. Su valor aproximado es 1.8541. Véase tabla de integrales elípticas de primera especie (Puig Adam P., Cálculo Integral. Editorial Biblioteca Matemática 1972, pág. 72)
>> k2=1/2; >> ellipke(k2) ans = 1.8541
En la figura, se muestra cómo el periodo P depende de la amplitud A
- La curva en color rojo, la amplitud es A=0.3, el periodo es P=3.19 s
- La curva en color azul, la amplitud es A=0.15, el periodo es P=6.38 s
No hay comentarios:
Publicar un comentario