Grupos de Lie
función elemental es una función construida a partir de una cantidad finita de funciones elementales fundamentales y constantes mediante operaciones racionales (adición, sustracción, multiplicación y división)y la composición de funciones. Usando exponenciales, logarítmicas, potenciales,constantes, y las funciones trigonométricas y sus inversas, todas consideradas dentro del grupo de funciones elementales fundamentales.1
Las funciones elementales son un subconjunto del conjunto de las funciones generadas a partir de las funciones especiales, mediante operaciones elementales y composición.- ....................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=de7159df18baead092558b12d1b66348e9f7f127&writer=rdf2latex&return_to=Funci%C3%B3n+elemental
Una función integrada de una combinación finita de funciones constantes, las operaciones de campo ( además , multiplicación , división , yextracciones de raíces --el operaciones elementales ) - y algebraica, exponenciales y logarítmicas y sus inversas bajo composiciones repetidas (Shanks 1993, . p 145; Chow 1999). Entre las funciones elementales más simples son el logaritmo , función exponencial (incluyendo las funciones hiperbólicas ), potencia la función, y funciones trigonométricas .
Después de Liouville (1837, 1838, 1839), Watson (1966, p. 111) define los elementales funciones trascendentes como
(1)
| |||
(2)
| |||
(3)
|
y permite  , etc.
, etc.
No todas las funciones son elementales. Por ejemplo, la función de distribución normal
(4)
| |||
(5)
|
es un ejemplo notorio de una función no elemental, donde  es erf (a veces conocida como la función de error). La integral elíptica
es erf (a veces conocida como la función de error). La integral elíptica
(6)
|
es otro, donde  es una integral elíptica de primera especie .
es una integral elíptica de primera especie .
Ley de Brillouin
La función de Brillouin es una función especial definida por la siguiente ecuación:
Surge inicialmente de la descripción mecanocuántica de un paramagneto, y recibe su nombre del físico franco-estadounidense Léon Brillouin. En este contexto, J es el número cuántico demomento angular total y el parámetro  se define como:
se define como:
 se define como:
se define como:
Donde:
- m es el momento magnético de una partícula
- B es la intensidad del campo magnético
 es la constante de Boltzmann
es la constante de Boltzmann- T es la temperatura
- g es el factor de Landé
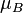 es el magnetón de Bohr
es el magnetón de Bohr
También en este contexto, la magnetización del sistema es:1
donde N es el número de átomos por unidad de volumen.
función cuadrática o función de segundo grado es una función polinómica definida por:
con  .1
.1
 .1
.1
Las gráficas de estas funciones corresponden a parábolas verticales (eje de simetría paralelo al eje de las ordenadas), con la particularidad de que cuando a>0, el vértice de la parábola se encuentra en la parte inferior de la misma, siendo un mínimo (es decir, la parábola se abre "hacia arriba"), y cuando a<0 abajo="" abre="" bola="" decir="" el="" en="" encuentra="" es="" hacia="" la="" m="" p="" par="" parte="" rtice="" se="" siendo="" superior="" un="" v="" ximo="">
El estudio de las funciones cuadráticas tiene numerosas aplicaciones en campos muy diversos, como por ejemplo la caída libre o el tiro parabólico.
La función derivada de una función cuadrática es una función lineal y su integral indefinida es una familia de funciones cúbicas.- ..........................................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=f1b6b0ab22ddc069e42b07d796f5c25cc23a0d83&writer=rdf2latex&return_to=Funci%C3%B3n+cuadr%C3%A1tica



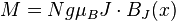

No hay comentarios:
Publicar un comentario