Superficie de Riemann
superficie de Riemann es una variedad compleja de dimensión (compleja) uno. Consecuentemente, la variedad real subyacente será de dimensión 2.- ..............................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=fab04d7ea7d2fdf7d3314ac1e24b73d0326cd156&writer=rdf2latex&return_to=Superficie+de+Riemann
geomeetría de superficies riemann .- ...........................:http://matmor.unam.mx/~muciray/articulos/Geometria_haces.pdf
glosario de la geometría de Riemann .- ..........................................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=5b0fd0053462745948538f025ff851ee5f25dc19&writer=rdf2latex&return_to=Anexo%3AGlosario+de+la+geometr%C3%ADa+de+Riemann
Esfera de Riemann
En matemática, la esfera de Riemann (o plano complejo extendido), llamada así en honor al matemático del siglo XIX Bernhard Riemann, es una esfera obtenida del plano complejo mediante la adición de un punto del infinito. La esfera es la representación geométrica de los números complejos extendidos, denotado como 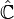 ó
ó  ,1 (véase fig.1y fig.2), la cual consiste en los números complejos ordinarios en conjunción con el símbolo
,1 (véase fig.1y fig.2), la cual consiste en los números complejos ordinarios en conjunción con el símbolo  para representar el infinito.
para representar el infinito.
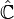 ó
ó  ,1 (véase fig.1y fig.2), la cual consiste en los números complejos ordinarios en conjunción con el símbolo
,1 (véase fig.1y fig.2), la cual consiste en los números complejos ordinarios en conjunción con el símbolo  para representar el infinito.
para representar el infinito.
Los números complejos extendidos son comunes en análisis complejoporque permiten la división por cero en algunas circunstancias, en el sentido de hacer expresiones tales como
bien definidas. Por ejemplo, cualquier función racional sobre el plano complejo puede ser extendida como una función continua sobre la esfera de Riemann, con los polos de la función racional mapeados al infinito. Más generalmente, cualquier función meromorfa puede ser pensada como una función continua cuyo codominio es la esfera de Riemann.
En geometría, la esfera de Riemann es el ejemplo prototípico de una superficie de Riemann, y una de las más simples variedades complejas. En geometría proyectiva, la esfera puede ser pensada como la recta proyectiva compleja  , el espacio proyectivo de todos las rectas complejas en
, el espacio proyectivo de todos las rectas complejas en 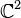 . Como con cualquier superficie de Riemann compacta, la esfera también puede ser vista como unacurva algebraica proyectiva, haciendo de esto un ejemplo fundamental de geometría algebraica. También encuentra utilidad en otras disciplinas que dependen del análisis y de la geometría, como puede ser la mecánica cuántica y otras ramas de la física.
. Como con cualquier superficie de Riemann compacta, la esfera también puede ser vista como unacurva algebraica proyectiva, haciendo de esto un ejemplo fundamental de geometría algebraica. También encuentra utilidad en otras disciplinas que dependen del análisis y de la geometría, como puede ser la mecánica cuántica y otras ramas de la física.
 , el espacio proyectivo de todos las rectas complejas en
, el espacio proyectivo de todos las rectas complejas en 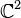 . Como con cualquier superficie de Riemann compacta, la esfera también puede ser vista como unacurva algebraica proyectiva, haciendo de esto un ejemplo fundamental de geometría algebraica. También encuentra utilidad en otras disciplinas que dependen del análisis y de la geometría, como puede ser la mecánica cuántica y otras ramas de la física.
. Como con cualquier superficie de Riemann compacta, la esfera también puede ser vista como unacurva algebraica proyectiva, haciendo de esto un ejemplo fundamental de geometría algebraica. También encuentra utilidad en otras disciplinas que dependen del análisis y de la geometría, como puede ser la mecánica cuántica y otras ramas de la física.
función meromorfa sobre un subconjunto abierto D del plano complejo es una función que es holomorfa en todo D excepto en un conjunto de puntos aislados, llamados polos de la función. (La terminología viene del Griego clásico “meros”, que significa parte, en contrapunto a “holos”, que significa todo.) Dichas funciones son a veces conocidas como funciones regulares oregulares sobre D.- ......................................................................................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=70841b8f491814b7246aab28a136a77b56fb1a99&writer=rdf2latex&return_to=Funci%C3%B3n+meromorfa
geometría hiperbólica (o lobachevskiana) es un modelo de geometría que satisface solo los cuatro primeros postulados de lageometría euclidiana. Aunque es similar en muchos aspectos y muchos de los teoremas de la geometría euclidiana siguen siendo válidos en geometría hiperbólica, no se satisface el quinto postulado de Euclides sobre las paralelas. Al igual que la geometría euclidiana y la geometría elíptica, la geometría hiperbólica es un modelo de curvatura constante:
- La geometría euclidiana satisface los cinco postulados de Euclides y tiene curvatura cero.
- La geometría hiperbólica satisface solo los cuatro primeros postulados de Euclides y tiene curvatura negativa.
- La geometría elíptica satisface solo los cuatro primeros postulados de Euclides y tiene curvatura positiva.- ..........................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=bc6f9921a3d5cd777cd6dab2b749f34aa87221af&writer=rdf2latex&return_to=Geometr%C3%ADa+hiperb%C3%B3lica
La geometría hiperbólica se construye sobre un espacio "curvado" y juega un importante papel en la teoría general de la relatividad de Einstein. La mayoría de los físicos de hoy día aceptan que nuestro Universo, considerado a gran escala, es un espacio hiperbólico de tres dimensiones que está curvado en su cuarta dimensión. La cuarta dimensión es una dirección distinta de las otras, no está ni arriba ni abajo, ni a la derecha ni a la izquierda, ni dentro ni fuera.
Es muy difícil imaginar un mundo de cuatro dimensiones. En 1884, Edwin Abbott publicó un libro, Flatland, que podemos traducir Planilandia, donde narraba las aventuras de un Cuadrado en un mundo plano de dos dimensiones. Podemos imaginar Planilandia como la superficie de un enorme lago tranquilo y a sus habitantes como figuras recortadas de una fina película plástica que se deslizan sobre el agua. Las dificultades que tiene el héroe del relato para entender el significado de una tercera dimensión, que sobrepasa las dos dimensiones del mundo en que está inmerso, pueden darnos una idea de nuestros propios problemas para percibir la 4ª dimensión de nuestro espacio.
Al comienzo de la historia, el Sr. Cuadrado y su esposa, la Sra. Triángulo, están descansando en su casa de dos dimensiones de Planilandia cuando se les aparece una Esfera, que trata de que comprendan la 3ª dimensión con una explicación como ésta:
"No soy una figura plana, sino un Sólido. Vosotros me llamáis Círculo, pero no soy un Círculo, sino un número infinito de Círculos colocados unos sobre otros, de distintos tamaños que varían entre un Punto y un Círculo de 13 pulgadas de diámetro. Cuando atravieso vuestro plano, como ahora, formo una sección que vosotros llamáis acertadamente Círculo. Porque si una Esfera -ese es mi nombre en mi país- se muestra ante un habitante de Planilandia, debe manifestarse como un Círculo""I am not a plane Figure, but a Solid. You call me a Circle; but in reality I am not a Circle, but an indefinite number of Circles, of size varying from a Point to a Circle of thirteen inches in diameter, one placed on the top of the other. When I cut through your plane as I am now doing, I make in your plane a section which you, very rightly, call a Circle. For even a Sphere - which is my proper name in my own country - if he manifest himself at all to an inhabitant of Flatland - must needs manifest himself as a Circle." [Abbott-1884]
En nuestro Universo, la curvatura de la 4ª dimensión se percibe de forma distinta según las diferentes escalas. Mientras que a pequeña escala la curvatura del espacio es muy pequeña y por ello la geometría euclídea tridimensional es apropiada para su estudio, a grandes escalas la curvatura del espacio es mayor y dicha geometría se muestra insuficiente, por lo que conviene utilizar la geometría hiperbólica para describirlo.
Para construir la geometría hiperbólica se mantienen invariables los cuatro primeros axiomas de Euclides, mientras que el 5º se sustituye por su negación, en la forma dada por la alternativa B que vimos en la introducción. Por ello, todos los resultados de Euclides que pueden deducirse a partir de los 4 primeros axiomas, sin utilizar el 5º, son también válidos en esta geometría. En cambio, otros resultados de la geometría hiperbólica pueden parecernos chocantes, como por ejemplo, quela suma de los ángulos de un triángulo hiperbólico es siempre menor que 180º.
Para facilitar el trabajo en ese espacio de cuatro dimensiones y ayudarnos a comprenderlo de alguna manera, suele comenzarse estudiando el espacio hiperbólico de dos dimensiones, que se representa mediante la superficie de una seudo-esfera. Podemos imaginar la superficie de una seudo-esfera como una trompeta ilimitada que forma un espacio de dos dimensiones, mayor que un plano y más "infinita" que él.
Hay un modelo especial de geometría hiperbólica, llamado Círculo de Poincaré, que consiste en "aplanar" la seudo-esfera sobre un círculo. Aunque la seudo-esfera se distorsiona por ese aplastamiento, lo hace de tal forma que conserva sus propiedades geométricas, y cualquier teorema obtenido en el modelo de Poincaré es igualmente válido sobre la seudo-esfera original.
El Círculo de Poincaré
Para desarrollar el modelo de Poincaré de geometría hiperbólica, comenzamos trazando en un plano coordenado una circunferencia C de centro en el origen y radio la unidad.
Definiremos los "P-puntos" de este modelo de Poincaré de geometría hiperbólica como los puntos que son interiores al círculo delimitado por C. Es decir, consideramos todos los puntos que pertenecen a dicho círculo, excepto los situados en la circunferencia C que forma la frontera.
Ahora definiremos las "P-rectas", que están formadas por los P-puntos de las líneas de cualquiera de los dos tipos siguientes:
- Diámetro de C.
- Arco de una circunferencia ortogonal a C. (Recordemos que dos circunferencias son ortogonales si las rectas tangentes en sus puntos de intersección son perpendiculares entre sí).
Es fácil convencerse de que este modelo cumple los dos axiomas 1 y 2 de la geometría de Euclides. Comenzaremos con el axioma 1, que, traducido al idioma de la geometría hiperbólica, dice así:"Dos P-puntos determinan una unica P-recta".
¿Cómo se traza la P-recta que pasa por dos P-puntos dados? Si hay algún diámetro de la circunferencia C que contenga a ambos puntos, como es el caso de A1 y B1 de la figura, dicho diámetro será la solución.
En otro caso, es decir, si los puntos no están alineados con el centro O de la circunferencia C, como ocurre con los puntos A y B de la figura, basta realizar los siguientes pasos:
1- Se traza la recta perpendicular a la recta OA por el punto A. Su intersección con la circunferencia C proporciona los puntos P y Q.
2- Se trazan las tangentes a la circunferencia C por P y Q. Ambas tangentes se cortan en el punto A´.
3- Se traza la circunferencia C´ que pasa por A, B y A´. Los puntos de C´, interiores al círculo limitado por C, forman la P-recta solución.
Así, las circunferencias C y C' son ortogonales. Puedes ver la demostración pinchando en el botón de Información Complementaria "i".
Para ver que se verifica el axioma 2, basta tener en cuenta que un P-segmento debe tener sus extremos en el interior de C, es decir, no pueden pertenecer nunca a la circunferencia frontera C, por tanto, por muy cercanos a ella que se encuentren sus extremos, siempre existe la posibilidad de prolongar más el P-segmento.
En cuanto al axioma de las paralelas, recordemos que rectas paralelas son las rectas de un mismo plano que no se cortan. Observemos la figura siguiente, en que las P-rectas AB y DE son paralelas, porque no tienen P-puntos comunes, como también lo son CB y DE. ¿Cuántas P-rectas paralelas a DE pasan por el P-punto B, exterior a dicha recta? En la figura vemos dos, las P-rectas AB y CB y podemos imaginar muchas otras. Por tanto, en este modelo de Poincaré, se verifica la negación del 5º axioma de Euclides en su alternativa B:
Dada una recta y un punto exterior a ella, existen al menos dos paralelas a la recta dada que contienen al punto.
El concepto de distancia entre dos puntos es básico para cualquier geometría. La distancia es una función que hace corresponder un número a cada par de puntos y debe cumplir las siguientes propiedades:
- Debe estar definida para todo par de puntos.
- La distancia será cero si los puntos coinciden. En otro caso, será positiva.
- La distancia entre A y B debe ser igual a la distancia entre B y A.
- Desigualdad triangular: Para A, B, y C, d(AC) ≤ d(AB) + d(BC).
- Debe ser continua, y para todo nº real x debe haber puntos A, B tales d(A,B)=x.
Daremos la siguiente definición de P-distancia: Sean P y Q dos P-puntos, que determinan una única P-recta que corta a la circunferencia frontera C en los puntos euclídeos A y B. La fórmula siguiente da la P-distancia entre P y Q a partir de las distancias euclídeas entre P y A, P y B, Q y A, Q y B:
A continuación veremos algunos P-segmentos de la misma P-longitud que nos resultarán chocantes porque nuestra intuición está acostumbrada a trabajar con sus longitudes euclídeas.
figura a)
|
figura b)
|
figura c)
|
Copyright©: Joel Castellanos, 1994-2001
Podemos observar que, cuando un punto se aproxima a la circunferencia que limita el círculo, su distancia al centro se aproxima a infinito. En la figura a) se muestran varios segmentos de P-recta, todos de igual P-longitud. Se aprecia que, cuanto más cercano a la circunferencia frontera se encuentra el segmento, más corto parece. Obsérvese que estos segmentos pueden considerarse radios de un P-círculo, puesto que tienen la misma P-longitud y un extremo común, que es su P-centro. Es decir, desde una óptica euclídea, vemos que el P-centro de un P-círculo parece estar "descentrado".
Los P-segmentos de la figura b) tienen todos un extremo en el centro de la circunferencia de Poincaré. Sus P-longitudes son: AB=0´25, AC=0´5, AD=1, ..., AJ=16 unidades. Es decir, según vamos en el sentido de las agujas del reloj, cada P-segmento es de doble P-longitud que el anterior. Así, aunque puedan parecernos casi iguales, las P-longitudes de AG y AJ son una doble de la otra.
En la figura c) aparecen dibujados varios triángulos que tienen idéntica superficie y forman una teselación del círculo de Poincaré.


No hay comentarios:
Publicar un comentario