Grupos de Lie
Función gamma
En matemáticas, la función gamma (denotada como 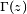 , donde
, donde  , es la "gamma mayúscula" del alfabeto griego) es una función que extiende el concepto de factorial a los números complejos. La notación fue ideada porAdrien-Marie Legendre. Si la parte real del número complejo z es positiva, entonces la integral
, es la "gamma mayúscula" del alfabeto griego) es una función que extiende el concepto de factorial a los números complejos. La notación fue ideada porAdrien-Marie Legendre. Si la parte real del número complejo z es positiva, entonces la integral
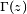 , donde
, donde  , es la "gamma mayúscula" del alfabeto griego) es una función que extiende el concepto de factorial a los números complejos. La notación fue ideada porAdrien-Marie Legendre. Si la parte real del número complejo z es positiva, entonces la integral
, es la "gamma mayúscula" del alfabeto griego) es una función que extiende el concepto de factorial a los números complejos. La notación fue ideada porAdrien-Marie Legendre. Si la parte real del número complejo z es positiva, entonces la integral
converge absolutamente; esta integral puede ser extendida a todo el plano complejo excepto a los enteros negativos y al cero. Si n es un entero positivo, entonces
lo que nos muestra la relación de esta función con el factorial. De hecho, la función Gamma generaliza el factorial para cualquier valor complejo de z. La función gamma aparece en varias funciones de distribución de probabilidad, por lo que es bastante usada tanto en probabilidad y estadística como en combinatoria.- ...................................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=06a05c563811b3bdded18f2adc45f72079c3460b&writer=rdf2latex&return_to=Funci%C3%B3n+gamma
La función gamma
La función gamma es a la vez una función simple e importante para el estudio de otras funciones en cursos avanzados de cálculo.
Factorial de un número
Recordaremos en primer lugar, el concepto de factorial de un número entero positivo n.
n!=n·(n-1)·(n-2)...3·2·1
MATLAB dispone de una función denominada factorial, aunque podemos calcularlo fácilmente con la funciónprod.
>> 1*2*3*4*5 ans = 120 >> factorial(5) ans = 120 >> prod(1:5) ans = 120
La función gamma
Se define del siguiente modo
Donde z puede ser un número real o complejo. En esta página solamente estudiaremos el caso en el que z sea real y positivo
Esta función es más complicada en la parte negativa de z, tiene asíntotas verticales para z=0, -1, -2, -3...
Representamos gráficamente la función gamma para z>0, llamando a la función del mismo nombre disponible en MATLAB.
>> x=0.1:0.01:4;
>> y=gamma(x);
>> plot(x,y,'r')
>> xlabel('x')
>> ylabel('\gamma(x)')
>> title('Función gamma')
Podemos calcular el mínimo de la función aproximadamente.
>> x=1:0.01:2; >> y=gamma(x); >> yp=diff(y); >> idx=find(abs(yp)<0 .0001="">> x(idx) ans = 1.4500 1.4600 >> y(idx) ans = 0.8857 0.8856
El mínimo se encuentra entre 1 y 2 en la posición x=1.46 y vale 0.8856.
Relaciones
Relacionamos Γ(z+1) con Γ(z)
Integrando por partes
Mediante esta relación calculamos el valor de la función gamma, para z=1,2,3,4,...
>> z=1:6; >> gamma(z) ans = 1 1 2 6 24 120
Calculamos la función Γ(z) para valores fraccionarios de z. Por ejemplo, para z=1/2
>> syms t; >> y=exp(-t)/sqrt(t); >> int(y,0,inf) ans =pi^(1/2)
Para calcular el valor de la integral hacemos el cambio t=y2.
Se puede consultar en la tablas el valor de esta integral, o resolverla del siguiente modo
Cambiamos de coordenadas rectangulares a polares. En coordendas polares el elemento diferencial de áreadx·dy=(r·dθ)dr
Finalmente, utilizando la relación anterior Γ(z+1)=z·Γ(z)
>> n=6; >> num=2*(1:n)-1; >> prod(num)*sqrt(pi)/2^n ans = 287.8853 >> gamma(n+1/2) ans = 287.8853
función gamma elíptica es una generalización de la función q-gamma, la cual es en si misma un q-análogo de lafunción gamma ordinaria. Está íntimamente relacionada con la función estudiada por Jackson (1905), y puede ser expresada en términos de la función gamma triple.Su representación es la siguiente:
Ésta obedece varias identidades:
y
donde θ es la función q-theta.
Cuando 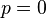 , ésta esencialmente se reduce al símbolo q-Pochhammer infinito:
, ésta esencialmente se reduce al símbolo q-Pochhammer infinito:
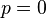 , ésta esencialmente se reduce al símbolo q-Pochhammer infinito:
, ésta esencialmente se reduce al símbolo q-Pochhammer infinito:
- función gamma incompleta se define como una integral definida del mismo integrando.Hay dos tipos de función gamma incompleta, una para el caso en el que varía el límite inferior de integración, y otro cuando varía el límite superior. La primera se denota como
 y se define comoLa segunda se escribe
y se define comoLa segunda se escribe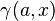 y se define comoEn ambos casos, x es una variable real mayor o igual que cero, y a es una variable compleja, cuya parte real es positiva.- ........................................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=8d1cb6f1e70bfddcb238f207ee27a5ca9f0b3f89&writer=rdf2latex&return_to=Funci%C3%B3n+gamma+incompleta
y se define comoEn ambos casos, x es una variable real mayor o igual que cero, y a es una variable compleja, cuya parte real es positiva.- ........................................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=8d1cb6f1e70bfddcb238f207ee27a5ca9f0b3f89&writer=rdf2latex&return_to=Funci%C3%B3n+gamma+incompleta



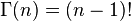


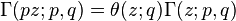
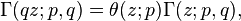


No hay comentarios:
Publicar un comentario