Variedad compleja
variedad compleja M es una variedad topológica que tiene la estructura que nos permite definir la noción de función holomorfa  .1
.1
 .1
.1
Ello se podrá conseguir por dos caminos:
- Exigiendo que exista un atlas (o conjunto de cartas) que recubra la variedad de modo que las funciones de transición (o cambios de cartas) sean holomorfas.
- O, de un modo menos directo, exigiendo la existencia sobre la variedad diferenciable subyacente de una estructura casi complejaJ (endomorfismo que verifica
 ) y una condición de integrabilidad.
) y una condición de integrabilidad.
Toda variedad compleja de dimensión compleja n será, en particular, también una variedad diferenciable de dimensión real 2n, orientable,2 y dotada de una orientación natural.3
Puesto que las funciones holomorfas son mucho más rígidas que las funciones diferenciables, la teoría de variedades complejas presenta importantes diferencias con la de variedades diferenciables.- ....................................................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=6aeaf109536cd010f610b8172dde16cd68a12306&writer=rdf2latex&return_to=Variedad+compleja
El matemático Eugenio Calabi conjeturó en 1957 que tales variedades admiten una métricacon curvatura de Ricci nula (una en cada clase de Kähler), es decir, una variedad "plana". Esta conjetura fue probada por Shing-Tung Yau en 1977 y devino el teorema de Yau. Por lo tanto, una variedad de Calabi-Yau se puede también definir como variedad Ricci-plana compacta de Kähler.
También es posible definir una variedad de Calabi-Yau como variedad con una holonomíaSU(n). Otra condición equivalente es que la variedad admite una (n, 0)-forma holomórfica global nunca nula.- ..........................................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=82663bcee4fc8d6afb598d52e81f1f178036bbb5&writer=rdf2latex&return_to=Variedad+de+Calabi-Yau
variedad de Kähler es una variedad con estructura unitaria a ( -estructura) que satisface una condición de integración. En particular, es una variedad compleja, una variedad de Riemann, y una variedad simpléctica, con estas tres estructuras compatibles entre sí.
-estructura) que satisface una condición de integración. En particular, es una variedad compleja, una variedad de Riemann, y una variedad simpléctica, con estas tres estructuras compatibles entre sí.
 -estructura) que satisface una condición de integración. En particular, es una variedad compleja, una variedad de Riemann, y una variedad simpléctica, con estas tres estructuras compatibles entre sí.
-estructura) que satisface una condición de integración. En particular, es una variedad compleja, una variedad de Riemann, y una variedad simpléctica, con estas tres estructuras compatibles entre sí.
Esta estructura triple corresponde a la presentación del grupo unitario como una intersección:
Sin ninguna condición de integración, la noción análoga es una variedad hermítica parcial. Si la estructura-Sp es integrable (sin que la estructura compleja lo sea), la noción es una variedad de Kähler parcial; si la estructura compleja es integrable (sin que la estructura-Sp lo sea), la noción es una variedad hermítica.- ................................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=91115757425434d7e14280401f4959ae418192c6&writer=rdf2latex&return_to=Variedad+de+K%C3%A4hler
variedades de Stein generalizan la noción de dominio de holomorfía en el espacio complejo n-dimensional incluyendo las subvariedades complejas cerradas de este espacio afín. Fueron introducidas por Karl Stein en 1951 y son relevantes para la geometría compleja por su flexibilidad en términos del principio de Oka y la geometría simpléctica por su equivalencia con lasvariedades Weinstein. En geometría holomorfa, i.e. compleja, las variedades de Stein son el análogo de la variedades afines en geometría algebraica.- ..................................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=152e9be51e83fd9e4831d8d1b7ff3904c39d1645&writer=rdf2latex&return_to=Variedad+de+Stein
variedad subriemanniana es un cierto tipo de generalización de una variedad de Riemann. A grandes rasgos, para medir distancias en una variedad subriemanniana, solo se permite moverse a través de curvas tangentes a los llamados subespacios horizontales.
Las variedades subriemannianas (y, a fortiori, también las variedades Riemannianas) poseen una métrica intrínseca llamada métrica de Carnot–Carathéodory. En estos espacios métricos, la dimensión de Hausdorff es siempre un entero más grande que su dimensión topológica (a menos que sea una variedad riemanniana propiamente).- ..............................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=c559ce78203115e04505d0caf98ba0f23c193d6b&writer=rdf2latex&return_to=Variedad+subriemanniana
variedades Weinstein son una clase de variedades simplécticas flexibles. Su estructura es tal que la rigidez que la estructura simpléctica podría imponer en hacer una operación topológica casi no aparece. Así, construcciones como las construcciones con handle-bodies o el h-principio funcionan para este tipo de variedades.Una variedad simpléctica 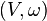 es una variedad Weinstein si admite un campo de Liouville X completo y una función de Morseexhaustiva de la variedad en R tal que el campo X sea pseudo-gradiente para la función. La estructura Weinstein se suele denotar
es una variedad Weinstein si admite un campo de Liouville X completo y una función de Morseexhaustiva de la variedad en R tal que el campo X sea pseudo-gradiente para la función. La estructura Weinstein se suele denotar 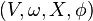
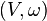 es una variedad Weinstein si admite un campo de Liouville X completo y una función de Morseexhaustiva de la variedad en R tal que el campo X sea pseudo-gradiente para la función. La estructura Weinstein se suele denotar
es una variedad Weinstein si admite un campo de Liouville X completo y una función de Morseexhaustiva de la variedad en R tal que el campo X sea pseudo-gradiente para la función. La estructura Weinstein se suele denotar 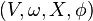
También se define la noción de dominio de Weinstein donde la variedad simpléctica es compacta con frontera de manera que el campo de Liouville apunta hacia el exterior de la frontera y la frontera está contenida en un conjunto de nivel de la función de Morse. En estos términos, una variedad de Weinstein se puede estudiar como la unión de dominios de Weinstein. Siendo más preciso, una variedad de Weinstein 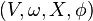 se puede ir estudiando analizando progresivamente los dominios de Weinstein
se puede ir estudiando analizando progresivamente los dominios de Weinstein  , entendiendo que ktoma siempre valores regulares.Un ejemplo clásico de variedad simpléctica es el fibrado cotangente. Sea V el fibrado cotangente de una variedad cerrada con la forma simpléctica canónica inducida por la forma de Liouville. Veamos que además admite una estructura Weinstein. Para eso consideramos una función de Morse f en la variedad base, acoplando el gradiente -con respecto a una métrica Riemanniana en la base- con la forma de Liouville obtenemos una función F. El campo suma del campo radial en los momentos junto con el campo asociado al Hamiltoniano Fes Liouville y es un pseudo-gradiente para la función de Morse suma de energía cinética y f.
, entendiendo que ktoma siempre valores regulares.Un ejemplo clásico de variedad simpléctica es el fibrado cotangente. Sea V el fibrado cotangente de una variedad cerrada con la forma simpléctica canónica inducida por la forma de Liouville. Veamos que además admite una estructura Weinstein. Para eso consideramos una función de Morse f en la variedad base, acoplando el gradiente -con respecto a una métrica Riemanniana en la base- con la forma de Liouville obtenemos una función F. El campo suma del campo radial en los momentos junto con el campo asociado al Hamiltoniano Fes Liouville y es un pseudo-gradiente para la función de Morse suma de energía cinética y f.
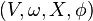 se puede ir estudiando analizando progresivamente los dominios de Weinstein
se puede ir estudiando analizando progresivamente los dominios de Weinstein  , entendiendo que ktoma siempre valores regulares.Un ejemplo clásico de variedad simpléctica es el fibrado cotangente. Sea V el fibrado cotangente de una variedad cerrada con la forma simpléctica canónica inducida por la forma de Liouville. Veamos que además admite una estructura Weinstein. Para eso consideramos una función de Morse f en la variedad base, acoplando el gradiente -con respecto a una métrica Riemanniana en la base- con la forma de Liouville obtenemos una función F. El campo suma del campo radial en los momentos junto con el campo asociado al Hamiltoniano Fes Liouville y es un pseudo-gradiente para la función de Morse suma de energía cinética y f.
, entendiendo que ktoma siempre valores regulares.Un ejemplo clásico de variedad simpléctica es el fibrado cotangente. Sea V el fibrado cotangente de una variedad cerrada con la forma simpléctica canónica inducida por la forma de Liouville. Veamos que además admite una estructura Weinstein. Para eso consideramos una función de Morse f en la variedad base, acoplando el gradiente -con respecto a una métrica Riemanniana en la base- con la forma de Liouville obtenemos una función F. El campo suma del campo radial en los momentos junto con el campo asociado al Hamiltoniano Fes Liouville y es un pseudo-gradiente para la función de Morse suma de energía cinética y f.
Dado un dominio de Weinstein podemos obtener una variedad de Weinstein añadiendo la variedad simplectizada de la frontera, que es una variedad de contacto. De hecho, una variedad de Weinstein tal que la función de Morse tiene un número finito de puntos críticos se puede obtener completando un dominio de Weinstein con la variedad simplectizada. En particular las variedades Weinstein dan lugar a ejemplos de variedades de contacto, cualquier conjunto de nivel de la función de Morse es de contacto.
Dadas dos variedades Weinstein es posible dotar el producto cartersiano de una estructura Weinstein de la forma natural.

No hay comentarios:
Publicar un comentario