lunes, 1 de diciembre de 2014

CARTOGRAFÍA


PROYECCIONES CARTOGRÁFICAS :
La proyección sinusoidal es una proyección cartográfica pseudocilíndrica de áreas equivalentes, también llamada proyección de Sanson-Flamsteed o Mercator de áreas iguales. Jean Cossin, de la escuela de cartografía de Dieppe] fue uno de los primeros cartógrafos en usar esta proyección, apareciendo ya en un mapa del mundo de 1570. Matemáticamente, ciene definida por la ecuación:
x = \left(\lambda - \lambda_0\right) \cos \phi
y = \phi\,
donde:
  • \phi\, es la latitud,
  • \lambda\, la longitud y
  • \lambda_0\, es el meridiano central

.-.............................................:http://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=ba26ec178bc962ffdb4125a3fef00aa547ddc8ad&writer=rdf2latex&return_to=Proyecci%C3%B3n+sinusoidal

 




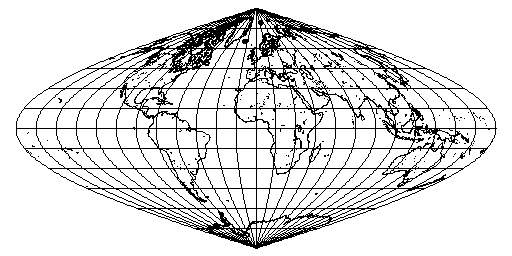
La proyección Werner es una proyección cartográfica pseudocónica de igual área para mapamundis, también llamada proyección Stab-Werner o Stabius-Werner. Al igual que otras proyecciones en forma de corazón, también se categoriza como cordiforme.
Esta proyección fue desarrollada por dos autores: Johannes Werner (1468-1522), párroco alemán de Nuremberg, hombre que promovió y refinó esta proyección que había sido desarrollada antes por un amigo y colaborador suyo, el cartógrafo austríacoJohannes Stabius (Stab) de Viena alrededor de 1500.
La proyección es una forma límite de la proyección de Bonne, que tiene su paralelo estándar en uno de los polos (90°N/S).1 2 Las distancias a lo largo de cada paralelo y a lo largo del meridiano central son correctas, al igual que todas las distancias desde el polo norte.
 
La proyección de Winkel-Tripel (Winkel III) es una proyección cartográfica azimutal modificada, una de tres proyecciones propuestas por Oswald Winkel en 1921. La proyección es la media aritmética entre laproyección cilíndrica equidistante y la proyección de Aitoff:1
x = \frac{\lambda \cos(\phi_1) + \frac{2 \cos(\phi)\sin\left(\frac{\lambda}{2}\right)}{\mathrm{sinc}(\alpha)}}{2}
y = \frac{\phi + \frac{\sin(\phi)}{\mathrm{sinc}(\alpha)}}{2}
donde \lambda es la longitud desde el meridiano central de la proyección, \phi es la latitud, \phi_1 es el paralelo estándar para la proyección equirectangular, y
\alpha = \arccos\left(\cos(\phi) \cos\left(\frac{\lambda}{2}\right)\right)\,
\mathrm{sinc}(\alpha) es la función sinc desnormalizada con la discontinuidad eliminada. En su propuesta, Winkel puso :
\phi_1 = \arccos\left(\frac{2}{\pi}\right)\,
La proyección de Winkel-Tripel con la Indicatriz de Tissotde deformación
No sorprende que no exista una fórmula cartográfica inversa establecida, y procesar la inversa numéricamente sea un tanto complicado.
Goldberg & Gott indican que podría decirse que la Winkel-Tripel es la mejor proyección conocida para representar el mundo entero, produciendo muy pequeños errores de distancia, pequeños errores de combinaciones de elipticidad y área, y menor asimetría estadística que cualquier otro mapa.2
En 1998, proyección de Winkel-Tripel reemplazó a la proyección de Robinson como proyección estándar para los mapamundis hechos por la National Geographic Society. Muchas instituciones educacionales y publicaciones siguieron el ejemplo de la National Geographic de adoptar la proyección.
 
Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)