ÓPTICA

la divergencia del haz es una medida angular del aumento en el diámetro o radio del haz con la distancia desde la apertura óptica o la apertura de la antena de la cual emerge el haz. El término es relevante solo en el " campo lejano ", lejos de cualquier foco del haz. Prácticamente hablando, sin embargo, el campo lejano puede comenzar físicamente cerca de la abertura radiante, dependiendo del diámetro de la abertura y la longitud de onda de operación.

La divergencia del haz se utiliza a menudo para caracterizar los rayos electromagnéticos en el régimen óptico, en los casos en que la abertura de la que emerge el haz es muy grande con respecto a la longitud de onda . Sin embargo, también se utiliza en la frecuencia de radio (RF) de banda para los casos en los que la antena es muy grande en relación con una longitud de onda.

La divergencia del haz generalmente se refiere a un haz de sección transversal circular, pero no necesariamente así. Un haz puede, por ejemplo, tener una sección transversal elíptica, en cuyo caso debe especificarse la orientación de la divergencia del haz, por ejemplo, con respecto al eje mayor o menor de la sección transversal elíptica.

La divergencia de un haz se puede calcular si se conoce el diámetro del haz en dos puntos separados lejos de cualquier foco ( D _i , D _f ) y la distancia ( l ) entre estos puntos. La divergencia del haz,$${\ displaystyle \ Theta}, es dado por

$${\ displaystyle \ Theta = 2 \ arctan \ left ({\ frac {D_ {f} -D_ {i}} {2l}} \ right).}

Si un haz colimado se enfoca con una lente , el diámetro$${\ displaystyle D_ {m}} del haz en el plano focal posterior de la lente está relacionado con la divergencia del haz inicial por

$${\ displaystyle \ Theta = {\ frac {D_ {m}} {f}}, \,}

donde f es la longitud focal de la lente. ^[1] Tenga en cuenta que esta medida es válida solo cuando el tamaño del haz se mide en el plano focal posterior de la lente, es decir, donde se encuentra el foco para un haz verdaderamente colimado, y no en el foco real del haz, lo que ocurriría Detrás del plano focal trasero para un haz divergente.

Como todos los haces electromagnéticos, los láseres están sujetos a divergencias, que se miden en miliradianes(mrad) o grados . Para muchas aplicaciones, es preferible un haz de menor divergencia. Si se descuida la divergencia debido a la mala calidad del haz, la divergencia de un rayo láser es proporcional a su longitud de onda e inversamente proporcional al diámetro del haz en su punto más estrecho. Por ejemplo, un láser ultravioleta que emite a una longitud de onda de 308 nm tendrá una divergencia más baja que un láser infrarrojo a 808 nm, si ambos tienen el mismo diámetro de haz mínimo. La divergencia de los rayos láser de buena calidad se modela utilizando las matemáticas de los rayos gaussianos .

Se dice que los rayos láser gaussianos están limitados por difracción cuando la divergencia de su haz radial$${\ displaystyle \ theta = \ Theta / 2}está cerca del valor mínimo posible, que está dado por ^[2]

$${\ displaystyle \ theta = {\ lambda \ over \ pi w},}

dónde $${\ displaystyle \ lambda} es la longitud de onda del láser y $${\ displaystyle w}es el radio de la viga en su punto más estrecho, que se denomina "cintura de viga". Este tipo de divergencia de haz se observa a partir de cavidades láser optimizadas. La información sobre la divergencia limitada por difracción de un haz coherente viene dada por la ecuación interferométrica N-slit .

Los expansores de haz son dispositivos ópticos que toman un haz de luz colimado y expanden su tamaño (o, usados ​​al revés, reducen su tamaño).

En la física del láser se utilizan como elementos de intracavidad o extracavidad. Pueden ser de naturaleza telescópica o prismática. En general, los expansores de haz prismáticos utilizan varios prismas y se conocen como expansores de haz de prisma múltiple.

Los expansores de haz telescópico incluyen telescopios refractantes y reflectantes . ^[1] Un telescopio refractor que se usa comúnmente es el telescopio galileano, que puede funcionar como un simple expansor de haz de luz colimada . La principal ventaja del diseño galileano es que nunca enfoca un haz colimado a un punto, por lo que los efectos asociados con una alta densidad de potencia, como la ruptura dieléctrica, son más evitables que con diseños de enfoque como el telescopio Keplerian . Cuando se utilizan como expansores de haz intracavitario, en resonadores láser, estos telescopios proporcionan expansión de haz bidimensional en el rango de 20 a 50. ^[1]

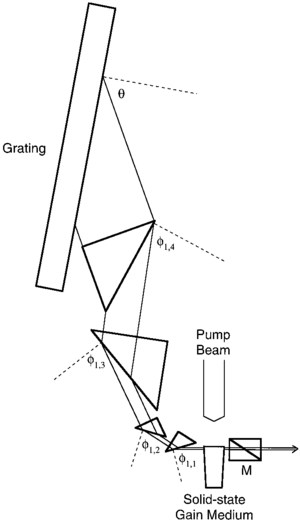
En los resonadores láser ajustables, la expansión del haz intracavitario generalmente ilumina todo el ancho de una rejilla de difracción . ^[2] Por lo tanto, la expansión del haz reduce la divergencia del haz y permite la emisión de anchos de línea muy estrechos ^[3], que es una característica deseada para muchas aplicaciones analíticas, incluida la espectroscopia láser.

Expansores de haz de prisma múltiple [ editar ]

Oscilador láser sintonizable de pulso largo que utiliza un expansor de haz de prisma múltiple ^[6]

Los expansores de haz de prisma múltiple generalmente implementan de dos a cinco prismas para producir grandes factores de expansión de haz unidimensional. Los diseños aplicables a láseres sintonizables con factores de expansión de haz de hasta 200 se han descrito en la literatura. ^[3]Inicialmente, las configuraciones de rejillas de prisma múltiple se introdujeron en láseres de tinte líquido de ancho de línea estrecho ^[1] [7] pero finalmente también se adoptaron en diseños de láser de diodo, de estado sólido y de gas. ^[3] La descripción matemática generalizada de los expansores de haz de prisma múltiple, introducida por Duarte , ^[8] se conoce como la teoría de la dispersión de prisma múltiple . ^[1] [3]

Los expansores de haz de prisma múltiple y las matrices también se pueden describir utilizando matrices de transferencia de rayos . ^[9] La teoría de la dispersión de prisma múltiple también está disponible en forma de matriz 4 X 4. ^[3] [10] Estas ecuaciones matriciales son aplicables tanto a compresores de prisma como a expansores de haz de prisma múltiple. ^[3]

Forma de viga extra cavidad [ editar ]

Transformadores de haz híbridos de cavidad extra: utilizando un expansor de haz telescópico, seguido de una lente convexa, seguido de un expansor de haz de prisma múltiple, un haz de láser (con una sección transversal circular) se puede transformar en un haz extremadamente alargado, en el plano de La propagación, aunque extremadamente delgada en el plano ortogonal. ^[3] [11] La iluminación del plano resultante, con una sección transversal casi unidimensional (o línea), elimina la necesidad de escaneo punto por punto y se ha convertido en importante para aplicaciones como la interferometría con ranura N , microdensitometría y La microscopía . Este tipo de iluminación también puede conocerse en la literatura como iluminación de lámina ligera o iluminación de plano selectiva.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Diagrama que muestra los vectores utilizados para definir el BRDF. Todos los vectores son de longitud unitaria.$${\ displaystyle \ omega _ {\ text {i}}} Apunta hacia la fuente de luz. $${\ displaystyle \ omega _ {\ text {r}}}Apunta hacia el espectador (cámara). $${\ displaystyle n} Es la superficie normal.

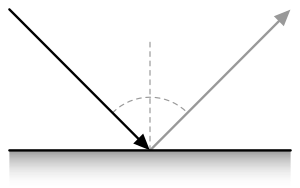
La función de distribución de reflectancia bidireccional ( BRDF ;$${\ displaystyle f _ {\ text {r}} (\ omega _ {\ text {i}}, \, \ omega _ {\ text {r}})} ) es una función de cuatro variables reales que definen cómo se refleja la luz en una superficie opaca . Se emplea en la óptica de la luz del mundo real, en los algoritmos de gráficos de computadora y en losalgoritmos de visión de computadora . La función toma una dirección de luz entrante,$${\ displaystyle \ omega _ {\ text {i}}}, y dirección saliente, $${\ displaystyle \ omega _ {\ text {r}}}(tomado en un sistema de coordenadas donde la superficie normal $${\ displaystyle \ mathbf {n}}se encuentra a lo largo del eje Z ), y devuelve la relación de la luminosidad reflejada que sale a lo largo$${\ displaystyle \ omega _ {\ text {r}}}a la irradiaciónincidente en la superficie desde la dirección$${\ displaystyle \ omega _ {\ text {i}}}. Cada direccion$${\ displaystyle \ omega}A su vez está parametrizado por el ángulo acimutal. $${\ displaystyle \ phi}y el ángulo cenital $${\ displaystyle \ theta}Por lo tanto, el BRDF en su conjunto es una función de 4 variables. El BRDF tiene unidades sr ⁻¹ , con esteradianos (sr) como una unidad de ángulo sólido .

Definición [ editar ]

El BRDF fue definido por primera vez por Fred Nicodemus alrededor de 1965. ^[1] La definición es:

$${\ displaystyle f _ {\ text {r}} (\ omega _ {\ text {i}}, \, \ omega _ {\ text {r}}) \, = \, {\ frac {\ operatorname {d} L _ {\ text {r}} (\ omega _ {\ text {r}})} {\ operatorname {d} E _ {\ text {i}} (\ omega _ {\ text {i}})}} \ , = \, {\ frac {\ operatorname {d} L _ {\ text {r}} (\ omega _ {\ text {r}})} {L _ {\ text {i}} (\ omega _ {\ text {i}}) \ cos \ theta _ {\ text {i}} \, \ operatorname {d} \ omega _ {\ text {i}}}}}

dónde $${\ displaystyle L}es la luminosidad , o la potencia por unidad de ángulo sólido, en la dirección de un rayo, por unidad de área proyectada, perpendicular al rayo,$${\ displaystyle E}es la irradiancia , o potencia por unidad de área de superficie , y$${\ displaystyle \ theta _ {\ text {i}}} es el ángulo entre $${\ displaystyle \ omega _ {\ text {i}}}y la superficie normal ,$${\ displaystyle \ mathbf {n}}. El índice$${\ displaystyle {\ text {i}}} Indica luz incidente, mientras que el índice. $${\ displaystyle {\ text {r}}} Indica la luz reflejada.

La razón por la cual la función se define como un cociente de dos diferenciales y no directamente como un cociente entre las cantidades no diferenciadas, se debe a que hay otra luz irradiadora que$${\ displaystyle \ operatorname {d} E _ {\ text {i}} (\ omega _ {\ text {i}})}, que no son de interes para $${\ displaystyle f _ {\ text {r}} (\ omega _ {\ text {i}}, \, \ omega _ {\ text {r}})}, podría iluminar la superficie que afectaría involuntariamente $${\ displaystyle L _ {\ text {r}} (\ omega _ {\ text {r}})}, mientras que $${\ displaystyle \ operatorname {d} L _ {\ text {r}} (\ omega _ {\ text {r}})} solo se ve afectado por $${\ displaystyle \ operatorname {d} E _ {\ text {i}} (\ omega _ {\ text {i}})}.

Funciones relacionadas [ editar ]

La función de distribución de reflectancia bidireccional que varía espacialmente (SVBRDF) es una función de 6 dimensiones,$${\ displaystyle f _ {\ text {r}} (\ omega _ {\ text {i}}, \, \ omega _ {\ text {r}}, \, \ mathbf {x})}, dónde $${\ displaystyle \ mathbf {x}} describe una ubicación 2D sobre la superficie de un objeto.

La función de textura bidireccional ( BTF ) es adecuada para modelar superficies no planas y tiene la misma parametrización que el SVBRDF; Sin embargo, en contraste, el BTF incluye efectos de dispersión no locales como sombreado, enmascaramiento, interreflexiones o dispersión subsuperficial . Las funciones definidas por el BTF en cada punto de la superficie se llaman BRDF aparentes .

La función de distribución de reflectancia de dispersión de superficie bidireccional ( BSSRDF , por sus siglas en inglés ) es una función de 8 dimensiones más generalizada.$${\ displaystyle S (\ mathbf {x} _ {\ text {i}}, \, \ omega _ {\ text {i}}, \, \ mathbf {x} _ {\ text {r}}, \, \ omega _ {\ text {r}})} en la cual la luz que ingresa a la superficie puede dispersarse internamente y salir a otra ubicación.

En todos estos casos, la dependencia de la longitud de onda de la luz se ha ignorado y agrupado en canales RGB . En realidad, el BRDF es dependiente de la longitud de onda, y para tener en cuenta los efectos como la iridiscencia o la luminiscencia, la dependencia de la longitud de onda debe hacerse explícita:$${\ displaystyle f _ {\ text {r}} (\ lambda _ {\ text {i}}, \, \ omega _ {\ text {i}}, \, \ lambda _ {\ text {r}}, \ , \ omega _ {\ text {r}})}. Tenga en cuenta que en el caso típico donde todos los elementos ópticos son lineales , la función obedecerá$${\ displaystyle f _ {\ text {r}} (\ lambda _ {\ text {i}}, \, \ omega _ {\ text {i}}, \, \ lambda _ {\ text {r}}, \ , \ omega _ {\ text {r}}) = 0} excepto cuando $${\ displaystyle \ lambda _ {\ text {i}} = \ lambda _ {\ text {r}}}: es decir, solo emitirá luz en longitud de onda igual a la luz entrante. En este caso puede parametrizarse como$${\ displaystyle f _ {\ text {r}} (\ lambda, \, \ omega _ {\ text {i}}, \, \ omega _ {\ text {r}})}, con un solo parámetro de longitud de onda.

BRDFs basados ​​físicamente [ editar ]

Los BRDF físicamente realistas tienen propiedades adicionales, ^{[2] que} incluyen,

• positividad $${\ displaystyle f _ {\ text {r}} (\ omega _ {\ text {i}}, \, \ omega _ {\ text {r}}) \ geq 0}
• obedeciendo la reciprocidad de Helmholtz :$${\ displaystyle f _ {\ text {r}} (\ omega _ {\ text {i}}, \, \ omega _ {\ text {r}}) = f _ {\ text {r}} (\ omega _ { \ text {r}}, \, \ omega _ {\ text {i}})}
• conservando energía: $${\ displaystyle \ forall \ omega _ {\ text {i}}, \, \ int _ {\ Omega} f _ \ \ text {r}} (\ omega _ {\ text {i}}, \, \ omega _ {\ text {r}}) \, \ cos {\ theta _ {\ text {r}}} d \ omega _ {\ text {r}} \ leq 1}

Aplicaciones [ editar ]

El BRDF es un concepto radiométrico fundamental y, en consecuencia, se utiliza en gráficos de computadorapara la representación fotorrealista de escenas sintéticas (ver la ecuación de representación ), así como en la visión por computadora para muchos problemas inversos , como el reconocimiento de objetos . BRDF también se ha utilizado para modelar la captura de luz en células solares (p. Ej., Mediante el uso del formalismo OPTOS ) o sistemas solares fotovoltaicos de baja concentración . ^[3] [4]

En el contexto de la detección remota por satélite, la NASA utiliza un modelo BRDF para caracterizar la anisotropía de superficie. Para un área de terreno dada, el BRDF se establece en base a observaciones multiangulares seleccionadas de reflectancia de superficie. Si bien las observaciones individuales dependen de la geometría de la vista y del ángulo solar, el producto MODIS BRDF / Albedo describe las propiedades intrínsecas de la superficie en varias bandas espectrales, a una resolución de 500 metros. ^[5] El producto BRDF / Albedo se puede utilizar para modelar el albedo de superficie en función de la dispersión atmosférica.

Modelos [ editar ]

Los BRDF se pueden medir directamente a partir de objetos reales utilizando cámaras y fuentes de luz calibradas; ^[6] sin embargo, se han propuesto muchos modelos fenomenológicos y analíticos, incluido el modelo de reflectancia de Lambert , frecuentemente asumido en gráficos de computadora. Algunas características útiles de los modelos recientes incluyen:

• acomodando la reflexión anisotrópica
• Editable utilizando un pequeño número de parámetros intuitivos.
• teniendo en cuenta los efectos de Fresnel en los ángulos de pastoreo
• Estar bien adaptado a los métodos de Monte Carlo .

W. Matusik et al. encontró que la interpolación entre muestras medidas produjo resultados realistas y fue fácil de entender. ^[7]

Difuso

Lustroso

Espejo

Tres componentes elementales que pueden usarse para modelar una variedad de interacciones luz-superficie. ^[8] El rayo de luz entrante se muestra en negro, el rayo (s) reflejado (s) modelado por el BRDF en gris.

• Modelo de Lambert , que representa superficies perfectamente difusas (mate) por un BRDF constante.
• Lommel – Seeliger , reflexión lunar y marciana.
• Modelo de reflectancia de Phong , un modelo fenomenológico similar a la especularidad similar al plástico. ^[9]
• Modelo de Blinn-Phong , parecido a Phong, pero que permite interpolar ciertas cantidades, lo que reduce la sobrecarga de cómputo. ^[10]
• El modelo Torrance-Sparrow, un modelo general que representa superficies como distribuciones de microfacetas perfectamente especulares. ^[11]
• Modelo Cook-Torrance , un modelo de microfaceta especular (Torrance-Sparrow) que representa la longitud de onda y, por lo tanto, el cambio de color. ^[12]
• Modelo Ward , un modelo de microfaceta especular con una función de distribución elíptica-gaussiana que depende de la orientación tangente de la superficie (además de la normal de la superficie). ^[13]
• El modelo de Oren-Nayar , un modelo de microfaceta "difusa dirigida", con microfacetas perfectamente difusas (en lugar de especulares). ^[14]
• Modelo Ashikhmin- Shirley , que permite la reflectancia anisotrópica, junto con un sustrato difuso bajo una superficie especular. ^[15]
• HTSG (He, Torrance, Sillion, Greenberg), un modelo integral basado en la física. ^[dieciséis]
• El modelo Lafortune ajustado, una generalización de Phong con múltiples lóbulos especulares, y está diseñado para ajustes paramétricos de datos medidos. ^[17]
• Modelo de Lebedev para aproximación BRDF analítica-rejilla. ^[18]

Adquisición [ editar ]

Tradicionalmente, los dispositivos de medición de BRDF llamados goniorreflectómetros emplean uno o más brazos goniométricos para colocar una fuente de luz y un detector en varias direcciones desde una muestra plana del material a medir. Para medir un BRDF completo, este proceso debe repetirse muchas veces, moviendo la fuente de luz cada vez para medir un ángulo de incidencia diferente. ^[19] Desafortunadamente, usar un dispositivo de este tipo para medir densamente el BRDF requiere mucho tiempo. Una de las primeras mejoras en estas técnicas utilizó un espejo semi plateado y una cámara digital para tomar muchas muestras de BRDF de un objetivo planar a la vez. Desde este trabajo, muchos investigadores han desarrollado otros dispositivos para la adquisición eficiente de BRDF a partir de muestras del mundo real, y sigue siendo un área activa de investigación.

Hay una forma alternativa de medir BRDF basado en imágenes HDR . El algoritmo estándar es medir la nube de puntos BRDF a partir de imágenes y optimizarla mediante uno de los modelos BRDF. ^[20]

Fabricación BRDF [ editar ]

Un ejemplo de fabricación BRDF

La fabricación de un patrón BRDF comienza con un boceto en bruto de una forma que deseamos que se forme la distribución general BRDF de la superficie. Existen muchas formas de realizar dicha tarea, pero en general podemos resumir los pasos a continuación:

• Transformar la forma de destino a una distribución BRDF.
• Pruebe esta distribución para discretizarla y hacer factible la fabricación.
• Diseñar una geometría de microfibra que produzca esta distribución.
• Optimizar esta superficie en cuanto a continuidad y suavidad de la superficie. (Este paso debe realizarse con respecto al procedimiento de fabricación)

Hay muchas formas de fabricar el producto final. Una forma es moler estas microfacetas en la superficie. ^[21] La distribución final de BRDF es la convolución del sustrato y la geometría de la superficie fresada. Otra forma es usar material con diferentes propiedades de reflectancia como los colores y usar medios tonos para producir el patrón. Al combinar estos dos métodos, podemos utilizar impresoras 3D para fabricar la geometría y cubrir la superficie con una sustancia adecuada, esto nos puede dar mayor libertad de diseño y posiblemente patrones de reflectancia más precisos.