ÓPTICA

número de Abbe , también conocido como el V-número o constringenciade un transparente de material, es una medida de del material de dispersión (variación de refracción índice frente a longitud de onda), con valores altos de V que indican una baja dispersión. Lleva el nombre de Ernst Abbe(1840–1905), el físico alemán que lo definió.

Variación del índice de refracción para el vidrio de pedernal SF-11 (gráfico superior), el vidrio de borosilicato BK-7 (curva media) y el cuarzo fundido (curva discontinua).

El número de Abbe, ^[1] [2] V _D , de un material se define como

$${\ displaystyle V_ {D} = {\ frac {n_ {D} -1} {n_ {F} -n_ {C}}},}

donde n _D , n _F y n _C son los índices de refracción del material en las longitudes de onda de las líneas espectrales Fraunhofer D, F y C (589.3 nm , 486.1 nm y 656.3 nm, respectivamente).

Los números de Abbe se utilizan para clasificar el vidrio y otros materiales ópticos en términos de su cromaticidad. Por ejemplo, los vidrios de pedernal de dispersión más alta tienen V  <55 font="" los="" mientras="" nbsp="" que="">vidrios de corona dedispersión más baja tienen números de Abbe más grandes. Los valores de V varían desde menos de 25 para vidrios de pedernal muy densos, alrededor de 34 para plásticos de policarbonato , hasta 65 para vidrios de copa comunes y de 75 a 85 para algunos vidrios de corona de fluorita y fosfato.

La mayor parte de la curva de sensibilidad de la longitud de onda del ojo humano, que se muestra aquí, está rodeada por las longitudes de onda de referencia del número Abbe de 486.1 nm (azul) y 656.3 nm (rojo)

Los números de Abbe se utilizan en el diseño de lentes acromáticas , ya que su recíproco es proporcional a la dispersión (pendiente del índice de refracción frente a la longitud de onda) en la región de longitud de onda donde el ojo humano es más sensible (ver gráfico). Para diferentes regiones de longitud de onda, o para una mayor precisión en la caracterización de la cromaticidad de un sistema (como en el diseño de apocromáticos ), se utiliza la relación de dispersión total (índice de refracción en función de la longitud de onda).

Abbe diagrama [ editar ]

Un diagrama de Abbe, también conocido como 'el velo de vidrio', traza el número de Abbe contra el índice de refracción para un rango de diferentes lentes (puntos rojos). Las gafas se clasifican utilizando el código de número de letra Schott Glass para reflejar su composición y posición en el diagrama.

Influencias de las adiciones de componentes de vidrio seleccionados en el número de Abbe de un vidrio base específico. ^[3]

Un diagrama de Abbe , también llamado 'el velo de cristal', se produce al trazar el número de Abbe V _d de un material contra su índice de refracción n _d . Las gafas se pueden clasificar y seleccionar de acuerdo con sus posiciones en el diagrama. Puede ser un código de número de letra, como se usa en el catálogo de Schott Glass , o un código de vidrio de 6 dígitos .

Los números de Abbe de Glasses, junto con sus índices refractivos medios, se utilizan en el cálculo de los poderes refractivos requeridos de los elementos de las lentes acromáticaspara cancelar la aberración cromática al primer orden. Tenga en cuenta que estos dos parámetros que entran en las ecuaciones para el diseño de dobletes acromáticos son exactamente lo que se representa en un diagrama de Abbe.

Debido a la dificultad y la inconveniencia de producir líneas de sodio e hidrógeno, a menudo se sustituyen definiciones alternativas del número de Abbe ( ISO 7944). ^[4] En lugar de la definición estándar, más arriba, usando la variación del índice de refracción entre las líneas de hidrógeno F y C , una medida alternativa que usa el subíndice "e"

$${\ displaystyle V_ {e} = {\ frac {n_ {e} -1} {n_ {F '} - n_ {C'}}}}

toma la diferencia entre los índices de refracción de las líneas de cadmio azul y rojo a 480.0 nm y 643.8 nm (con n _e refiriéndose a la longitud de onda de la línea e de mercurio, 546.073 nm). Otras definiciones pueden emplearse de manera similar; La siguiente tabla enumera las longitudes de onda estándar en las que n se determina comúnmente, incluidos los subíndices estándar empleados. ^[5]

λ en nm	Símbolo de fraunhofer	Fuente de luz	Color
365.01	yo	Hg	UV-A
404.66	h	Hg	Violeta
435.84	sol	Hg	azul
479.99	F'	Discos compactos	azul
486.13	F	H	azul
546.07	mi	Hg	verde
587.56	re	Él	amarillo
589.3	re	N / A	amarillo
643.85	DO'	Discos compactos	rojo
656.27	do	H	rojo
706.52	r	Él	rojo
768.2	UNA'	K	IR-A
852.11	s	Cs	IR-A
1013.98	t	Hg	IR-A

Este artículo necesita citas adicionales para su verificación . Por favor, ayudar a mejorar este artículo mediante la adición de citas de fuentes confiables . El material sin fuente puede ser desafiado y eliminado.  Encuentre fuentes:  "Condición sine de Abbe"  -  noticias  · periódicos  · libros  · erudito  ·JSTOR ( diciembre de 2009 ) ( Aprenda cómo y cuándo eliminar este mensaje de plantilla)

Los ángulos de entrada y salida de cada rayo que pasa a través de un sistema de imágenes (recuadro gris) están relacionados. Cuando el sistema de imágenes obedece a la condición sinusoidal de Abbe, la proporción de los senos de estos ángulos es igual a la ampliación (lateral absoluta) del sistema.

La condición sinusoidal de Abbe es una condición que debe cumplir una lente u otro sistema óptico para que pueda producir imágenes nítidas de objetos fuera del eje y en el eje. Fue formulado por Ernst Abbe en el contexto de los microscopios . ^[1]

La condición sine de Abbe dice que

el seno del ángulo del objeto-espacio$${\ textstyle \ alpha _ {o}} Debe ser proporcional al seno del ángulo del espacio de la imagen. $${\ textstyle \ alpha _ {i}}

Además, la relación es igual a la ampliación del sistema. En términos matemáticos esto es:

$${\ displaystyle {\ frac {\ sin \ alpha _ {o}} {\ sin \ alpha _ {i}}} = {\ frac {\ sin \ beta _ {o}} {\ sin \ beta _ {i} }} = | M |}

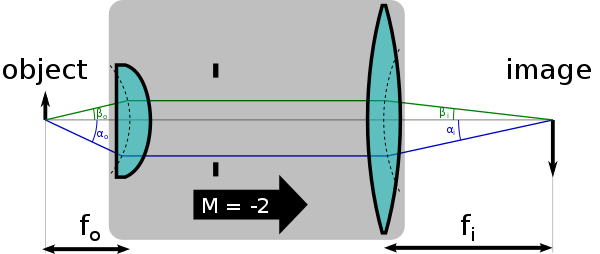
donde las variables $${\ textstyle (\ alpha _ {o}, \ beta _ {o})} son los ángulos (en relación con el eje óptico) de cualquiera de los dos rayos cuando salen del objeto, y $${\ textstyle (\ alpha _ {i}, \ beta _ {i})}son los ángulos de los mismos rayos donde alcanzan el plano de la imagen (por ejemplo, el plano de película de una cámara). Por ejemplo, ($${\ textstyle \ alpha _ {o}, \ alpha _ {i})}podría representar un rayo paraxial (es decir, un rayo casi paralelo al eje óptico), y$${\ textstyle (\ beta _ {o}, \ beta _ {i})}podría representar un rayo marginal (es decir, un rayo con el ángulo más grande admitido por la apertura del sistema). Se dice que un sistema de imágenes ópticas para el cual esto es cierto para todos los rayos obedece la condición de seno de Abbe.

La ampliación y la condición sinusoidal de Abbe [ editar ]

Un sistema óptico de imágenes (caja gris) que obedece a la condición sinusoidal tiene una relación fija entre los senos de los ángulos de los rayos en la entrada y la salida del sistema. $${\ textstyle {\ frac {\ sin \ alpha _ {o}} {\ sin \ alpha _ {i}}} = M}. Esta relación es igual a la ampliación (M).

Usando el marco de la óptica de Fourier , podemos explicar fácilmente el significado de la condición sinusoidal de Abbe. Decir que un objeto en el plano de objeto de un sistema óptico tiene una función de transmisión de la forma, T ( x _o , y _o ). Podemos expresar esta función de transmisión en términos de su transformada de Fourier como

$${\ displaystyle T (x_ {o}, y_ {o}) = \ iint T (k_ {x}, k_ {y}) ~ e ^ {j (k_ {x} x_ {o} + k_ {y} y_ {o})} ~ dk_ {x} \, dk_ {y}.}

Ahora, supongamos por simplicidad que el sistema no tiene distorsión de la imagen , de modo que las coordenadas del plano de la imagen están relacionadas linealmente con las coordenadas del plano del objeto a través de la relación

$${\ displaystyle x_ {i} = Mx_ {o} \,}

$${\ displaystyle y_ {i} = Mi_ {o} \,}

donde M es la ampliación del sistema . La transmitancia del plano del objeto anterior puede ahora reescribirse en una forma ligeramente modificada:

$${\ displaystyle T (x_ {o}, y_ {o}) = \ iint T (k_ {x}, k_ {y}) ~ e ^ {j ((k_ {x} / M) (Mx_ {o}) + (k_ {y} / M) (My_ {o}))} ~ dk_ {x} \, dk_ {y}}

donde los diversos términos se han multiplicado y dividido simplemente en el exponente por M , la ampliación del sistema. Ahora, las ecuaciones se pueden sustituir por las coordenadas del plano de la imagen en términos de coordenadas del plano del objeto, para obtener,

$${\ displaystyle T (x_ {i}, y_ {i}) = \ iint T (k_ {x}, k_ {y}) ~ e ^ {j ((k_ {x} / M) x_ {i} + ( k_ {y} / M) y_ {i})} ~ dk_ {x} \, dk_ {y}}

En este punto se puede proponer otra transformación de coordenadas ( i . E ., La condición sine Abbe) relativa el plano del objeto número de onda del espectro para el plano de imagen de número de onda del espectro como

$${\ displaystyle k_ {x} ^ {i} = {\ frac {k_ {x}} {M}}}

$${\ displaystyle k_ {y} ^ {i} = {\ frac {k_ {y}} {M}}}

para obtener la ecuación final para el campo del plano de la imagen en términos de coordenadas del plano de la imagen y números de referencia del plano de la imagen como:

$${\ displaystyle T (x_ {i}, y_ {i}) = M ^ {2} \ iint T (Mk_ {x} ^ {i}, Mk_ {y} ^ {i}) ~ e ^ {j (k_ {x} ^ {i} x_ {i} + k_ {y} ^ {i} y_ {i})} dk_ {x} ^ {i} \, dk_ {y} ^ {i}}

A partir de la óptica de Fourier , se sabe que los números de onda se pueden expresar en términos del sistema de coordenadas esféricas como

$${\ displaystyle k_ {x} = k \ sin \ theta \ cos \ varphi \,}

$${\ displaystyle k_ {y} = k \ sin \ theta \ sin \ varphi \,}

Si se considera un componente espectral para el cual $${\ displaystyle \ varphi = 0}, entonces la transformación de coordenadas entre el objeto y el plano de imagen wavenumbers toma la forma

$${\ displaystyle k ^ {i} \ sin \ theta ^ {i} = k {\ frac {\ sin \ theta} {M}}.

Esta es otra forma de escribir la condición sinusoidal de Abbe, que simplemente refleja el principio de incertidumbre clásico para los pares de transformadas de Fourier, a saber, que a medida que se amplía la extensión espacial de cualquier función (por el factor de ampliación, M ), la extensión espectral se contrae de la misma manera. Factor, M , de modo que el producto de ancho de banda espacial permanezca constante.