LISTAS RELACIONADAS CON LAS MATEMÁTICAS - ALGORITMOS

Quickselect es un algoritmo de selección para encontrar el k -ésimo elemento más pequeño de una lista desordenada. Está relacionado con el algoritmo de ordenación rápida . Al igual que Quicksort, fue desarrollado por Tony Hoare y, por lo tanto, también se conoce como el algoritmo de selección de Hoare . ^[1] Al igual que Quicksort, es eficiente en la práctica y tiene un buen rendimiento promedio de casos, pero tiene un rendimiento pobre en el peor de los casos. Quickselect y sus variantes son los algoritmos de selección más utilizados en implementaciones eficientes del mundo real.

Quickselect utiliza el mismo enfoque general que quicksort, eligiendo un elemento como pivote y dividiendo los datos en dos en función del pivote, en consecuencia, como menor o mayor que el pivote. Sin embargo, en lugar de recurrir en ambos lados, como en el ordenamiento rápido, la selección rápida solo se repite en un lado: el lado con el elemento que está buscando. Esto reduce la complejidad promedio de O ( n log n ) a O ( n ) , con el peor de los casos de O ( n ² ) .

Al igual que con quicksort, quickselect generalmente se implementa como un algoritmo in situ , y más allá de seleccionar el elemento k , también clasifica parcialmente los datos. Consulte el algoritmo de selección para obtener más información sobre la conexión con la clasificación.

Selección rápida

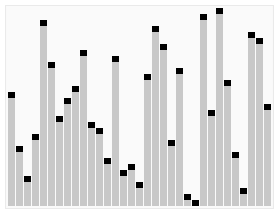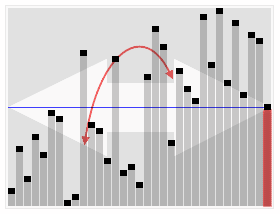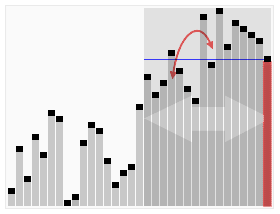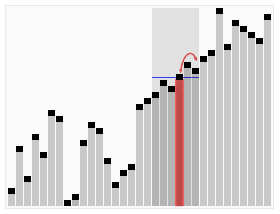
Visualización animada del algoritmo de selección rápida. Selección del valor 22 más pequeño.
Clase	Algoritmo de selección
Estructura de datos	Formación
El peor de los casos	О ( n 2 )
El mejor rendimiento	О ( n )
Rendimiento medio	O ( n )

Algoritmo [ editar ]

En quicksort, hay un subprocedimiento llamado partición que puede, en tiempo lineal, agrupar una lista (desde índices lefthasta right) en dos partes: las que son menores que un determinado elemento y las que son mayores o iguales al elemento. Aquí hay un seudocódigo que realiza una partición sobre el elemento list[pivotIndex]:

 partición de función (lista, izquierda, derecha, pivotIndex)
     pivotValue: = list [pivotIndex]
     swap list [pivotIndex] y list [right]   // Mover el pivote al final
     storeIndex: = left
     para i de izquierda a derecha-1
          si list [i] 
             intercambiar lista [storeIndex] y lista [i]
             Incrementar storeIndex
     intercambie la lista [derecha] y la lista [storeIndex]   // Mueva el pivote a su lugar final 
     return storeIndex

Esto se conoce como el esquema de partición de Lomuto , que es más simple pero menos eficiente que el esquema de partición original de Hoare .

En el ordenamiento rápido, ordenamos recursivamente ambas ramas, lo que lleva al mejor tiempo O ( n log n ). Sin embargo, al hacer la selección, ya sabemos en qué partición se encuentra nuestro elemento deseado, ya que el pivote está en su posición ordenada final, con todos los que lo preceden en un orden no ordenado y todos los que lo siguen en un orden no ordenado. Por lo tanto, una sola llamada recursiva localiza el elemento deseado en la partición correcta, y construimos sobre esto para la selección rápida:

  // Devuelve el k-ésimo elemento más pequeño de la lista dentro de left..right inclusive 
  // (es decir, left <= k <= right). 
  // El espacio de búsqueda dentro de la matriz está cambiando para cada ronda, pero la lista 
  // sigue siendo del mismo tamaño. Por lo tanto, k no necesita actualizarse con cada ronda. 
  función select (list, left, right, k)
      if left = right         // Si la lista contiene solo un elemento, 
         return list [left]   // devuelve ese elemento 
     pivotIndex: = ...      // selecciona un pivotIndex entre left y right , 
                            // por ejemplo, left + floor (rand ()% (right - left + 1))
     pivotIndex: = partición (lista, izquierda, derecha, pivotIndex)
     // El pivote está en su posición final ordenada 
     si k = pivotIndex
          return list [k]
      más si k return select (list, left, pivotIndex - 1, k)
      else 
         return select (list, pivotIndex + 1, right, k )

---

Tenga en cuenta la semejanza con el ordenamiento rápido: así como el algoritmo de selección basado en el mínimo es un ordenamiento de selección parcial, este es un ordenamiento rápido parcial, que genera y divide solo O (log n ) de sus particiones O ( n ). Este procedimiento simple ha esperado un rendimiento lineal y, como quicksort, tiene un rendimiento bastante bueno en la práctica. También es un algoritmo en el lugar , que requiere solo una sobrecarga de memoria constante si la optimización de llamada de cola está disponible, o si se elimina la recursión de cola con un bucle:

 función seleccionar (lista, izquierda, derecha, k)
      bucle 
         si izquierda = derecha
              lista de retorno [izquierda]
         pivotIndex: = ...      // seleccione pivotIndex entre izquierda y derecha
         pivotIndex: = partición (lista, izquierda, derecha, pivotIndex)
         if k = pivotIndex
              return list [k]
          sino if k 
             derecha: = pivotIndex - 1
         más
             izquierda: = pivotIndex + 1

Complejidad del tiempo [ editar ]

Al igual que quicksort, la selección rápida tiene un buen rendimiento promedio, pero es sensible al pivote que se elige. Si se eligen buenos pivotes, es decir, aquellos que disminuyen constantemente el conjunto de búsqueda en una fracción dada, entonces el conjunto de búsqueda disminuye exponencialmente en tamaño y por inducción (o sumando la serie geométrica ) se ve que el rendimiento es lineal, ya que cada paso es lineal y el tiempo total es un tiempo constante (dependiendo de qué tan rápido se reduzca el conjunto de búsqueda). Sin embargo, si los pivotes incorrectos se eligen constantemente, como la disminución de un solo elemento cada vez, el peor de los casos es cuadrático: O ( n ² ). Esto ocurre, por ejemplo, en la búsqueda del elemento máximo de un conjunto, utilizando el primer elemento como pivote y teniendo datos ordenados.

Variantes [ editar ]

La solución más fácil es elegir un pivote aleatorio, que produce un tiempo lineal casi seguro . Determinísticamente, uno puede usar la estrategia de pivote de mediana de 3 (como en la clasificación rápida), que produce un rendimiento lineal en datos parcialmente ordenados, como es común en el mundo real. Sin embargo, las secuencias inventadas pueden causar la peor complejidad posible; David Musser describe una secuencia de "asesino medio de 3" que permite un ataque contra esa estrategia, que fue una de las motivaciones de su algoritmo de introselección .

Se puede asegurar un rendimiento lineal incluso en el peor de los casos mediante el uso de una estrategia de pivote más sofisticada; Esto se hace en el algoritmo de la mediana de las medianas . Sin embargo, la sobrecarga de calcular el pivote es alta y, por lo tanto, esto generalmente no se usa en la práctica. Se puede combinar la selección rápida básica con la mediana de las medianas como alternativa para obtener un rendimiento promedio rápido del caso y un rendimiento lineal en el peor de los casos; Esto se hace en introselect .

Los cálculos más precisos de la complejidad del tiempo promedio producen el peor caso de $${\ displaystyle n (2 + 2 \ log 2 + o (1)) \ leq 3.4n + o (n)}para pivotes aleatorios (en el caso de la mediana; otros k son más rápidos). ^[2] La constante se puede mejorar a 3/2 mediante una estrategia de pivote más complicada, que genera el algoritmo Floyd-Rivest , que tiene una complejidad promedio de$${\ displaystyle 1.5n + O (n ^ {1/2})}para mediana, con otros k siendo más rápidos.

introselect (abreviatura de "selección introspectiva") es un algoritmo de selección que es un híbrido de selección rápida y mediana de medianas que tiene un rendimiento promedio rápido y un rendimiento óptimo en el peor de los casos. Introselect está relacionado con el algoritmo de clasificación de introsort : estos son refinamientos análogos de la selección rápida básica y la clasificación rápidaalgoritmos, en el sentido de que ambos comienzan con el algoritmo rápido, que tiene un buen rendimiento promedio y una baja sobrecarga, pero recurre a un algoritmo óptimo en el peor de los casos (con una sobrecarga más alta) si el algoritmo rápido no progresa lo suficientemente rápido. David Musser introdujo ambos algoritmos ( Musser 1997 ), con el propósito de proporcionar algoritmos genéricos para la Biblioteca estándar de C ++ que tienen un rendimiento promedio rápido y un rendimiento óptimo en el peor de los casos, lo que permite que los requisitos de rendimiento sean más estrictos. ^[1]Sin embargo, en la mayoría de las implementaciones de la Biblioteca estándar de C ++ que usan introselect, se utiliza otro algoritmo "introselect", que combina selección rápida y heapselect, y tiene el peor tiempo de ejecución de O ( n log n ) ^[2] .

Algoritmos [ editar ]

Introsort logra un rendimiento práctico comparable al de clasificación rápida al tiempo que preserva el comportamiento de O ( n log n ) en el peor de los casos al crear un híbrido de clasificación rápida y ordenamiento dinámico . Introsort comienza con quicksort, por lo que alcanza un rendimiento similar al de quicksort si quicksort funciona, y vuelve a apilar (que tiene un rendimiento óptimo en el peor de los casos) si quicksort no progresa lo suficientemente rápido. Del mismo modo, introselect combina la selección rápida con la mediana de las medianas para lograr la selección lineal en el peor de los casos con un rendimiento similar a la selección rápida.

Introselect funciona al comenzar de manera optimista con la selección rápida y solo cambiar al algoritmo de selección de tiempo lineal en el peor de los casos (el algoritmo de mediana de Blum-Floyd-Pratt-Rivest-Tarjan ) si se repite demasiadas veces sin progresar lo suficiente. La estrategia de conmutación es el contenido técnico principal del algoritmo. Simplemente limitar la recursividad a una profundidad constante no es lo suficientemente bueno, ya que esto haría que el algoritmo cambie a todas las listas suficientemente grandes. Musser analiza un par de enfoques simples:

• Mantenga un registro de la lista de tamaños de las subparticiones procesadas hasta ahora. Si en algún momento se han realizado k llamadas recursivas sin reducir a la mitad el tamaño de la lista, para algunos pequeños k positivos , cambie al algoritmo lineal en el peor de los casos.
• Suma el tamaño de todas las particiones generadas hasta ahora. Si esto excede el tamaño de la lista multiplicado por alguna pequeña constante positiva k , cambie al algoritmo lineal en el peor de los casos. Esta suma es fácil de rastrear en una sola variable escalar.

Ambos enfoques limitan la profundidad de recursión a k ⌈log n ⌉ = O (log n ) y el tiempo total de ejecución a O ( n) .

El documento sugería que se realizarían más investigaciones sobre introselect, pero el autor se retiró en 2007 sin haber publicado ninguna investigación adicional.

búsqueda lineal o secuencial es un método para encontrar un elemento dentro de una lista . Comprueba secuencialmente cada elemento de la lista hasta que se encuentra una coincidencia o se ha buscado en toda la lista. ^[1]

Una búsqueda lineal se ejecuta en el peor tiempo lineal y realiza como máximo n comparaciones, donde n es la longitud de la lista. Si cada elemento tiene la misma probabilidad de ser buscado, entonces la búsqueda lineal tiene un caso promedio de n/2 comparaciones, pero el caso promedio puede verse afectado si las probabilidades de búsqueda para cada elemento varían. La búsqueda lineal rara vez es práctica porque otros algoritmos y esquemas de búsqueda, como el algoritmo de búsqueda binaria y las tablas hash , permiten una búsqueda significativamente más rápida para todas las listas, excepto las cortas.

Algoritmo [ editar ]

Una búsqueda lineal verifica secuencialmente cada elemento de la lista hasta que encuentra un elemento que coincida con el valor objetivo. Si el algoritmo llega al final de la lista, la búsqueda finaliza sin éxito. ^[1]

Algoritmo básico [ editar ]

Dada una lista L de n elementos con valores o registros L ₀ .... L _n -1 , y el valor objetivo T , la siguiente subrutina utiliza búsqueda lineal para encontrar el índice del objetivo T en L . ^[3]

1. Establezca i en 0.
2. Si L _i = T , la búsqueda termina con éxito; volver i .
3. Aumentar i en 1.
4. Si i < n , vaya al paso 2. De lo contrario, la búsqueda finaliza sin éxito.

Con un centinela [ editar ]

El algoritmo básico anterior hace dos comparaciones por iteración: uno para comprobar si L _i es igual a T , y el otro para comprobar si yo aún apunta a un índice válido de la lista. Al agregar un registro adicional L _n a la lista (un valor centinela ) que iguala el objetivo, la segunda comparación se puede eliminar hasta el final de la búsqueda, haciendo que el algoritmo sea más rápido. La búsqueda llegará al centinela si el objetivo no está incluido en la lista. ^[4]

1. Establezca i en 0.
2. Si L _i = T , vaya al paso 4.
3. Aumente i en 1 y vaya al paso 2.
4. Si i < n , la búsqueda finaliza con éxito; volver i . De lo contrario, la búsqueda termina sin éxito.

En una tabla ordenada [ editar ]

Si la lista se ordena de manera que L ₀ ≤ L ₁ ... ≤ L _n −1 , la búsqueda puede establecer la ausencia del objetivo más rápidamente al concluir la búsqueda una vez que L _i excede el objetivo. Esta variación requiere un centinela que es mayor que el objetivo. ^[5]

1. Establezca i en 0.
2. Si L _i ≥ T , vaya al paso 4.
3. Aumente i en 1 y vaya al paso 2.
4. Si L _i = T , la búsqueda termina con éxito; volver i . De lo contrario, la búsqueda termina sin éxito.

Análisis [ editar ]

Para una lista con n elementos, el mejor caso es cuando el valor es igual al primer elemento de la lista, en cuyo caso solo se necesita una comparación. El peor de los casos es cuando el valor no está en la lista (o ocurre solo una vez al final de la lista), en cuyo caso se necesitan n comparaciones.

Si el valor que se busca aparece k veces en la lista, y todos los ordenamientos de la lista son igualmente probables, el número esperado de comparaciones es

{\ displaystyle {\ begin {cases} n & {\ mbox {if}} k = 0 \\ [5pt] \ displaystyle {\ frac {n + 1} {k + 1}} & {\ mbox {if}} 1 \ leq k \ leq n. \ end {cases}}}

Por ejemplo, si el valor que se busca aparece una vez en la lista, y todos los ordenamientos de la lista son igualmente probables, el número esperado de comparaciones es $${\ displaystyle {\ frac {n + 1} {2}}}. Sin embargo, si se sabe que ocurre una vez, entonces, como máximo , se necesitan n - 1 comparaciones, y el número esperado de comparaciones es

$${\ displaystyle \ displaystyle {\ frac {(n + 2) (n-1)} {2n}}}

(por ejemplo, para n = 2 esto es 1, correspondiente a una sola construcción if-then-else).

De cualquier manera, asintóticamente , el costo del peor de los casos y el costo esperado de la búsqueda lineal son O ( n ).

Probabilidades no uniformes [ editar ]

El rendimiento de la búsqueda lineal mejora si el valor deseado tiene más probabilidades de estar cerca del comienzo de la lista que de su final. Por lo tanto, si es más probable que se busquen algunos valores que otros, es conveniente colocarlos al principio de la lista.

En particular, cuando los elementos de la lista están organizados en orden de probabilidad decreciente, y estas probabilidades están distribuidas geométricamente , el costo de la búsqueda lineal es solo O (1). ^[6]

Solicitud [ editar ]

La búsqueda lineal suele ser muy sencilla de implementar, y es práctica cuando la lista tiene solo unos pocos elementos, o cuando se realiza una búsqueda única en una lista no ordenada.

Cuando se deben buscar muchos valores en la misma lista, a menudo vale la pena preprocesar la lista para utilizar un método más rápido. Por ejemplo, uno puede ordenar la lista y usar la búsqueda binaria , o construir una estructura de datos de búsqueda eficiente a partir de ella. Si el contenido de la lista cambia con frecuencia, la reorganización repetida puede ser más problemática de lo que vale.

Como resultado, aunque en teoría otros algoritmos de búsqueda pueden ser más rápidos que la búsqueda lineal (por ejemplo, la búsqueda binaria ), en la práctica incluso en matrices de tamaño mediano (alrededor de 100 elementos o menos) podría no ser factible usar cualquier otra cosa. En matrices más grandes, solo tiene sentido usar otros métodos de búsqueda más rápidos si los datos son lo suficientemente grandes, porque el tiempo inicial para preparar (ordenar) los datos es comparable a muchas búsquedas lineales.