AMIGOS PARA SIEMPRE: LISTAS RELACIONADAS CON LAS MATEMÁTICAS

el algoritmo de Hirschberg , que lleva el nombre de su inventor, Dan Hirschberg , es un algoritmo de programación dinámico que encuentra la alineación de secuencia óptima entre dos cadenas . La óptima se mide con la distancia de Levenshtein , definida como la suma de los costos de inserciones, reemplazos, eliminaciones y acciones nulas necesarias para cambiar una cadena en la otra. El algoritmo de Hirschberg se describe simplemente como una versión más eficiente del espacio del algoritmo Needleman-Wunsch que usa divide y vencerás . ^[1] El algoritmo de Hirschberg se usa comúnmente enbiología computacional para encontrar alineamientos globales máximos de secuencias de ADN y proteínas .

Información de algoritmo [ editar ]

El algoritmo de Hirschberg es un algoritmo generalmente aplicable para la alineación de secuencia óptima. BLAST y FASTA son heurísticas subóptimas . Si x e y son cadenas, donde longitud ( x ) = ny longitud ( y ) = m , el algoritmo Needleman-Wunsch encuentra una alineación óptima en el tiempo O ( nm ), utilizando el espacio O ( nm ). El algoritmo de Hirschberg es una modificación inteligente del algoritmo Needleman-Wunsch que todavía toma tiempo O ( nm ), pero solo necesita O (min { n , m}) espacio y es mucho más rápido en la práctica. ^[2] Una aplicación del algoritmo es encontrar alineamientos de secuencias de ADN o secuencias de proteínas. También es una forma de espacio eficiente para calcular la subsecuencia común más larga entre dos conjuntos de datos, como con la herramienta diff común .

El algoritmo de Hirschberg puede derivarse del algoritmo Needleman-Wunsch observando que: ^[3]

se puede calcular el puntaje de alineación óptimo almacenando solo la fila actual y anterior de la matriz de puntaje de Needleman-Wunsch;
Si $(Z,W)=\operatorname {NW} (X,Y)$ es la alineación óptima de $(X,Y)$ y $X=X^{l}+X^{r}$ es una partición arbitraria de , existe una partición $Y^{l}+Y^{r}$ de tal que $\operatorname {NW} (X,Y)=\operatorname {NW} (X^{l},Y^{l})+\operatorname {NW} (X^{r},Y^{r})$ .

Descripción del algoritmo [ editar ]

X_{i}

denota el carácter i-ésimo de

, dónde

1<i\leqslant \operatorname {length} (X)

X_{i:j}

denota una subcadena de tamaño

j-i+1

, que van desde el i-ésimo al j-ésimo carácter de

\operatorname {rev} (X)

es la versión inversa de

son secuencias a alinear Dejar

ser un personaje de

. Asumimos que

\operatorname {Del} (x)

\operatorname {Ins} (y)

\operatorname {Sub} (x,y)

son funciones bien definidas con valores enteros. Estas funciones representan el costo de eliminar

, insertando

y reemplazando

con

, respectivamente.

Definimos

\operatorname {NWScore} (X,Y)

, que devuelve la última línea de la matriz de puntuación de Needleman-Wunsch

\mathrm {Score} (i,j)

 función NWScore (X, Y)
   Matriz de puntuación (0,0) = 0 // 2 * longitud (Y)
   para j = 1 a la longitud (Y)
     Score (0, j) = Score (0, j-1) + Ins (Y _j )
    para i = 1 a length (X) // init array
     Puntuación (1,0) = Puntuación (0,0) + Supr (X _i )
      para j = 1 a la longitud (Y)
       scoreSub = Puntuación (0, j-1) + Sub (X _i , Y _j )
       scoreDel = Score (0, j) + Del (X _i )
       scoreIns = Score (1, j-1) + Ins (Y _j )
       Score (1, j) = max (scoreSub, scoreDel, scoreIns)
     final
     // copia Puntuación [1] a Puntuación [0]
     Puntuación (0, :) = Puntuación (1, :)
   final 
   para j = 0 a la longitud (Y)
     LastLine (j) = Puntuación (1, j)
   volver LastLine

Tenga en cuenta que en cualquier momento,

\operatorname {NWScore}

solo requiere las dos filas más recientes de la matriz de puntaje. Así,

\operatorname {NWScore}

se implementa en

O(\operatorname {min} \{\operatorname {length} (X),\operatorname {length} (Y)\})

espacio

El algoritmo de Hirschberg sigue:

 función Hirschberg (X, Y)
   Z = ""
   W = ""
   si longitud (X) == 0
      para i = 1 a longitud (Y)
       Z = Z + '-'
       W = W + Y _i
     termino 
   else if longitud (Y) == 0
      para i = 1 a la longitud (X)
       Z = Z + X _i
       W = W + '-'
     terminar 
   si la longitud (X) == 1 o longitud (Y) == 1
     (Z, W) = NeedlemanWunsch (X, Y)
   más
     xlen = longitud (X)
     xmid = longitud (X) / 2
     ylen = longitud (Y)
 
     ScoreL = NWScore (X _{1: xmid} , Y)
     ScoreR = NWScore (rev (X _{xmid + 1: xlen} ), rev (Y))
     ymid = arg max ScoreL + rev (ScoreR)
 
     (Z, W) = Hirschberg (X _{1: xmid} , y _{1: ymid} ) + Hirschberg (X _{xmid + 1: xlen} , Y _{ymid + 1: ylen} )
    retorno final
    (Z, W)

En el contexto de la Observación (2), suponga que

X^{l}+X^{r}

es una partición de

. Índice

\mathrm {ymid}

se calcula de manera que

Y^{l}=Y_{1:\mathrm {ymid} }

Y^{r}=Y_{\mathrm {ymid} +1:\operatorname {length} (Y)}

Ejemplo [ editar ]

Dejar

{\begin{aligned}X&=\mathrm {AGTACGCA} ,\\Y&=\mathrm {TATGC} ,\\\operatorname {Del} (x)&=-2,\\\operatorname {Ins} (y)&=-2,\\\operatorname {Sub} (x,y)&={\begin{cases}+2,&{\mbox{if }}x=y\\-1,&{\mbox{if }}x\neq y.\end{cases}}\end{aligned}}

La alineación óptima viene dada por

 W = AGTACGCA
 Z = --TATGC-

De hecho, esto se puede verificar haciendo un seguimiento de su matriz de Needleman-Wunsch correspondiente:

         TATGC 
     0   -2 -4 -6 -8 -10
  A   -2   -1 0 -2 -4 -6
  G   -4   -3 -2 -1 0 -2
  T   -6   -2   -4 0 -2 -1
  A   - 8 -4    0   -2 -1 -3
  C -10 -6 -2   -1   -3 1
  G -12 -8 -4 -3    1   -1
  C -14 -10 -6 -5 -1    3 
 A -16 - 12 -8 -7 -3    1

Uno comienza con la llamada de nivel superior a

\operatorname {Hirschberg} (\mathrm {AGTACGCA} ,\mathrm {TATGC} )

, que divide el primer argumento a la mitad:

X=\mathrm {AGTA} +\mathrm {CGCA}

. La llamada a

\operatorname {NWScore} (\mathrm {AGTA} ,Y)

produce la siguiente matriz:

        TATGC
    0 -2 -4 -6 -8 -10
 A -2 -1 0 -2 -4 -6
  G -4 -3 -2 -1 0 -2
  T -6 -2 -4 0 -2 -1
  A -8 -4 0 -2 -1 -3

Igualmente,

\operatorname {NWScore} (\operatorname {rev} (\mathrm {CGCA} ),\operatorname {rev} (Y))

genera la siguiente matriz:

       CGTAT
    0 -2 -4 -6 -8 -10
 A -2 -1 -3 -5 -4 -6
  C -4 0 -2 -4 -6 -5
  G -6 -2 2 0 -2 -4
  C -8 -4 0 1 -1 -3

Sus últimas líneas (después de invertir la última) y la suma de ellas son respectivamente

 Puntuación L = [-8 -4 0 1 -1 -3]
 rev (ScoreR) = [-3 -1 1 0 -4 -8]
 Suma = [-11 -5   1   1 -5 -11]

El máximo (mostrado en negrita) aparece en ymid = 2 , produciendo la partición

Y=\mathrm {TA} +\mathrm {TGC}

Toda la recursión de Hirschberg (que omitimos por brevedad) produce el siguiente árbol:

               (AGTACGCA, TATGC)
               / \
        (AGTA, TA) (CGCA, TGC)
         / \ / \
     (AG,) (TA, TA) (CG, TG) (CA, C)
              / \ / \       
           (T, T) (A, A) (C, T) (G, G)

Las hojas del árbol contienen la alineación óptima.

algoritmo Needleman-Wunsch es un algoritmo utilizado en bioinformática para alinear secuencias de proteínas o nucleótidos . Fue una de las primeras aplicaciones de programación dinámica para comparar secuencias biológicas. El algoritmo fue desarrollado por Saul B. Needleman y Christian D. Wunsch y publicado en 1970. ^[1] El algoritmo esencialmente divide un gran problema (por ejemplo, la secuencia completa) en una serie de problemas más pequeños, y utiliza las soluciones a los más pequeños. problemas para encontrar una solución óptima al problema mayor. ^[2] También a veces se lo denomina algoritmo de correspondencia óptimo y eltécnica de alineación global . El algoritmo Needleman-Wunsch todavía se usa ampliamente para una alineación global óptima, particularmente cuando la calidad de la alineación global es de suma importancia. El algoritmo asigna una puntuación a cada alineación posible, y el propósito del algoritmo es encontrar todas las alineaciones posibles que tengan la puntuación más alta.

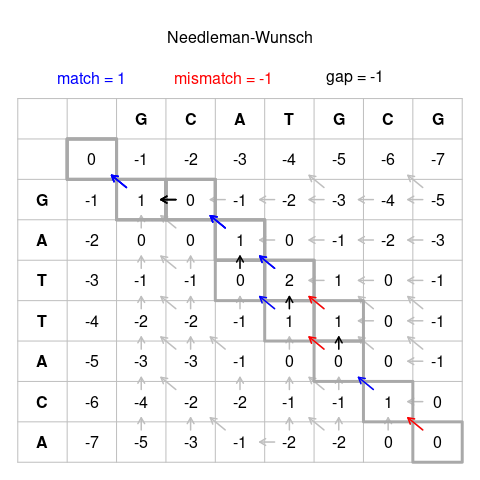
Figura 1: Alineación de secuencia por pares de Needleman-Wunsch

Resultados:

Secuencias Mejores alineaciones
--------- ----------------------
GCATGCU GCATG-CU GCA-TGCU GCATG-GCU
GATTACA G-ATTACA G-ATTACA G-ATTACA

Interpretación del paso de inicialización:

Uno puede interpretar la columna más a la izquierda en la figura anterior de esta manera (poniendo un "identificador" antes de cada secuencia, anotado como + aquí):

Alineamiento: + GCATGCU
            + GATTACA
Puntuación: 0 // El mango coincide con el mango, no gana ningún puntaje

Alineamiento: + GCATGCU
           + GATTACA
Puntuación: 0 // 1 hueco, puntuación -1

Alineamiento: + GCATGCU
          + GATTACA
Puntuación: 0 // 2 lagunas, puntuación -2

Alineamiento: + GCATGCU
         + GATTACA
Puntuación: 0 // 3 lagunas, puntuación -3

Alineamiento: + GCATGCU
        + GATTACA
Puntuación: 0 // 4 lagunas, puntuación -4

...

Lo mismo se puede hacer para la fila superior.


Introducción [ editar ]

Este algoritmo se puede usar para dos cadenas cualquiera . Esta guía utilizará dos pequeñas secuencias de ADN como ejemplos como se muestra en el diagrama:
GCATGCU
GATTACA


Construyendo la cuadrícula [ editar ]

Primero construya una cuadrícula como la que se muestra en la Figura 1 anterior. Comience la primera cadena en la parte superior de la tercera columna y comience la otra cadena al comienzo de la tercera fila. Complete el resto de los encabezados de columna y fila como en la Figura 1. Todavía no debe haber números en la cuadrícula.

sol do UNA T sol do U
  
sol 
UNA 
T 
T 
UNA 
do 
UNA 


Elegir un sistema de puntuación [ editar ]

Luego, decida cómo puntuar cada par de letras. Usando el ejemplo anterior, un posible candidato de alineación podría ser:
12345678
GCATG-CU
G-ATTACA


Las letras pueden coincidir, no coincidir o coincidir con un espacio (una eliminación o inserción ( indel )):

Coincidencia: las dos letras en el índice actual son las mismas.
No coinciden: las dos letras en el índice actual son diferentes.
Indel (INsertion o DELetion): la mejor alineación implica que una letra se alinee con un espacio en la otra cadena.


A cada uno de estos escenarios se le asigna un puntaje y la suma de los puntajes de todos los emparejamientos es el puntaje de todo el candidato de alineación. Existen diferentes sistemas para asignar puntajes; algunos se detallan en la sección de Sistemas de puntuación a continuación. Por ahora, se utilizará el sistema utilizado por Needleman y Wunsch ^[1] :

Partido: +1
No coinciden o Indel: −1


Para el ejemplo anterior, la puntuación de la alineación sería 0:
GCATG-CU
G-ATTACA
+ - ++ - + - -> 1 * 4 + (-1) * 4 = 0


Rellenando la tabla [ editar ]

Comience con un cero en la segunda fila, segunda columna. Desplácese por las celdas fila por fila, calculando el puntaje de cada celda. El puntaje se calcula comparando los puntajes de las celdas vecinas a la izquierda, arriba o arriba a la izquierda (diagonal) de la celda y agregando el puntaje apropiado para coincidencia, falta de coincidencia o indel. Calcule los puntajes candidatos para cada una de las tres posibilidades:

La ruta desde la celda superior o izquierda representa un emparejamiento indel, así que tome los puntajes de la celda izquierda y superior, y agregue el puntaje para indel a cada uno de ellos.
La ruta diagonal representa una coincidencia / falta de coincidencia, por lo tanto, tome la puntuación de la celda diagonal superior izquierda y agregue la puntuación para la coincidencia si las bases (letras) correspondientes en la fila y la columna coinciden o la puntuación para la falta de coincidencia si no lo hacen.


El puntaje resultante para la celda es el más alto de los tres puntajes candidatos.

Dado que no hay celdas 'superior' o 'superior izquierda' para la segunda fila, solo se puede usar la celda existente a la izquierda para calcular la puntuación de cada celda. Por lo tanto, se agrega -1 para cada cambio a la derecha, ya que esto representa un indeleble de la puntuación anterior. Esto da como resultado que la primera fila sea 0, -1, -2, -3, -4, -5, -6, -7. Lo mismo se aplica a la segunda columna, ya que solo se puede usar la puntuación existente sobre cada celda. Así, la tabla resultante es:

sol do UNA T sol do U
0 0 -1 -2 -3 -4 -5 -6 -7
sol -1 
UNA -2 
T -3 
T -4 
UNA -5 
do -6 
UNA -7 


El primer caso con puntajes existentes en las 3 direcciones es la intersección de nuestras primeras letras (en este caso G y G). Las celdas circundantes están a continuación:

sol
0 0 -1
sol -1 X


Esta celda tiene tres posibles sumas candidatas:

El vecino diagonal superior izquierdo tiene puntaje 0. El emparejamiento de G y G es una coincidencia, por lo tanto, agregue el puntaje para la coincidencia: 0 + 1 = 1
El vecino superior tiene un puntaje -1 y moverse desde allí representa un indel, así que agregue el puntaje para indel: (-1) + (-1) = (-2)
El vecino izquierdo también tiene un puntaje -1, representa un indel y también produce (-2).


El candidato más alto es 1 y se ingresa en la celda:

sol
0 0 -1
sol -1 1


La celda que dio el puntaje más alto del candidato también debe registrarse. En el diagrama completado en la figura 1 anterior, esto se representa como una flecha desde la celda en la fila y columna 3 a la celda en la fila y columna 2.

En el siguiente ejemplo, el paso diagonal para X e Y representa una falta de coincidencia:

sol do
0 0 -1 -2
sol -1 1 X
UNA -2 Y 


X:

Arriba: (-2) + (- 1) = (-3)
Izquierda: (+1) + (- 1) = (0)
Arriba a la izquierda: (-1) + (- 1) = (-2)


Y:

Arriba: (1) + (- 1) = (0)
Izquierda: (-2) + (- 1) = (-3)
Arriba a la izquierda: (-1) + (- 1) = (-2)


Tanto para X como para Y, la puntuación más alta es cero:

sol do
0 0 -1 -2
sol -1 1 0 0
UNA -2 0 0 


El puntaje más alto del candidato puede ser alcanzado por dos o todas las celdas vecinas:

T sol
T 1 1
UNA 0 0 X


Arriba: (1) + (- 1) = (0)
Arriba a la izquierda: (1) + (- 1) = (0)
Izquierda: (0) + (- 1) = (-1)


En este caso, todas las direcciones que alcanzan el puntaje de candidato más alto deben anotarse como posibles celdas de origen en el diagrama terminado en la figura 1, por ejemplo, en la celda en la fila y columna 7.

Completar la tabla de esta manera proporciona los puntajes o todos los posibles candidatos de alineación, el puntaje en la celda en la parte inferior derecha representa el puntaje de alineación para la mejor alineación.

Trazando flechas de regreso al origen [ editar ]

Marque una ruta desde la celda en la parte inferior derecha hacia la celda en la parte superior izquierda siguiendo la dirección de las flechas. A partir de este camino, la secuencia se construye mediante estas reglas:

Una flecha diagonal representa una coincidencia o falta de coincidencia, por lo que la letra de la columna y la letra de la fila de la celda de origen se alinearán.
Una flecha horizontal o vertical representa un indel. Las flechas horizontales alinearán un espacio ("-") con la letra de la fila (la secuencia "lateral"), las flechas verticales alinearán un espacio con la letra de la columna (la secuencia "superior").
Si hay varias flechas para elegir, representan una ramificación de las alineaciones. Si dos o más ramas pertenecen a rutas desde la celda inferior izquierda a la superior derecha, son alineaciones igualmente viables. En este caso, observe las rutas como candidatos de alineación separados.


Siguiendo estas reglas, los pasos para un posible candidato de alineación en la figura 1 son:
U → CU → GCU → -GCU → T-GCU → AT-GCU → CAT-GCU → GCAT-GCU 
A → CA → ACA → TACA → TTACA → ATTACA → -ATTACA → G-ATTACA
             ↓
    (rama) → TGCU → ...
             → TACA → ...


Sistemas de puntuación [ editar ]

Esquemas básicos de puntuación [ editar ]

Los esquemas de puntuación más simples simplemente dan un valor para cada coincidencia, desajuste e indel. La guía paso a paso anterior usa match = 1, mismatch = −1, indel = −1. Por lo tanto, cuanto menor sea el puntaje de alineación, mayor será la distancia de edición , para este sistema de puntaje uno quiere un puntaje alto. Otro sistema de puntuación podría ser:

Partido = 0
Indel = 1
No coincidencia = 1


Para este sistema, la puntuación de alineación representará la distancia de edición entre las dos cadenas. Se pueden diseñar diferentes sistemas de puntuación para diferentes situaciones, por ejemplo, si las brechas se consideran muy malas para su alineación, puede usar un sistema de puntuación que penalice las brechas en gran medida, como:

Partido = 0
No coincidencia = 1
Indel = 10


Probarlo .

Matriz de similitud [ editar ]

Los sistemas de puntuación más complicados atribuyen valores no solo para el tipo de alteración, sino también para las letras involucradas. Por ejemplo, se puede dar una coincidencia entre A y A 1, pero se puede dar una coincidencia entre T y T 4. Aquí (suponiendo el primer sistema de puntuación) se le da más importancia a la coincidencia Ts que a la As, es decir, la coincidencia Ts se supone que es más significativo para la alineación. Esta ponderación basada en letras también se aplica a los desajustes.

Para representar todas las combinaciones posibles de letras y sus puntuaciones resultantes, se utiliza una matriz de similitud. La matriz de similitud para el sistema más básico se representa como:

UNA sol do T
UNA 1 -1 -1 -1
sol -1 1 -1 -1
do -1 -1 1 -1
T -1 -1 -1 1


Cada puntaje representa un cambio de una de las letras que la celda coincide con la otra. Por lo tanto, esto representa todas las coincidencias y eliminaciones posibles (para un alfabeto de ACGT). Tenga en cuenta que todas las coincidencias van a lo largo de la diagonal, tampoco toda la tabla debe llenarse, solo este triángulo porque las puntuaciones son recíprocas. = (Puntuación para A → C = Puntuación para C → A). Si se implementa la regla TT = 4 desde arriba, se produce la siguiente matriz de similitud:

UNA sol do T
UNA 1 -1 -1 -1
sol -1 1 -1 -1
do -1 -1 1 -1
T -1 -1 -1 4 4


Se han construido estadísticamente diferentes matrices de puntuación que dan peso a diferentes acciones apropiadas para un escenario particular. Tener matrices de puntuación ponderadas es particularmente importante en la alineación de la secuencia de proteínas debido a la frecuencia variable de los diferentes aminoácidos. Hay dos familias amplias de matrices de puntuación, cada una con modificaciones adicionales para escenarios específicos:

PAM
BLOSUM


Penalización de hueco [ editar ]

Al alinear secuencias, a menudo hay huecos (es decir, indeles), a veces grandes. Biológicamente, es más probable que ocurra una gran brecha como una deleción grande en lugar de múltiples deleciones individuales. Por lo tanto, dos pequeños indeles deberían tener un puntaje peor que uno grande. La forma más simple y común de hacerlo es a través de una puntuación de inicio de brecha grande para un nuevo indel y una puntuación de extensión de brecha más pequeña para cada letra que extiende la indel. Por ejemplo, new-indel puede costar -5 y extend-indel puede costar -1. De esta forma una alineación como:
GAAAAAAT
G - AAT


que tiene múltiples alineaciones iguales, algunas con múltiples alineaciones pequeñas ahora se alinearán como:
GAAAAAAT
GAA ---- T


o cualquier alineación con un espacio de 4 largos de preferencia sobre múltiples espacios pequeños.

Presentación avanzada del algoritmo [ editar ]

Las puntuaciones para los caracteres alineados se especifican mediante una matriz de similitud . Aquí,  $S (un, b)$  es la similitud de caracteres una y b . Utiliza una penalización de hueco lineal , aquí llamada  $d$  .

Por ejemplo, si la matriz de similitud era

UNA sol do T
UNA 10 -1 -3 -4
sol -1 7 7 -5 -3
do -3 -5 9 9 0 0
T -4 -3 0 0 8


entonces la alineación:
AGACTAGTTAC
CGA --- GACGT


con una penalización de hueco de -5, tendría el siguiente puntaje:
 $S (A, C) + S (G, G) + S (A, A) + (3 \times d) + S (G, G) + S (T, A) + S (T, C) + S ( A, G) + S (C, T)$ 
= -3 + 7 + 10 - (3 × 5) + 7 + (-4) + 0 + (-1) + 0 = 1

Para encontrar la alineación con la puntuación más alta, se asigna una matriz bidimensional (o matriz ) F. La entrada en la fila i y la columna j se denota aquí por  $F_{ij}$ . Hay una fila para cada carácter en la secuencia A , y una columna para cada carácter en la secuencia B . Por lo tanto, si se alinean secuencias de tamaños n y m , la cantidad de memoria utilizada está en $O(nm)$ . El algoritmo de Hirschberg solo contiene un subconjunto de la matriz en la memoria y utiliza $\Theta (\min\{n,m\})$  espacio, pero por lo demás es similar a Needleman-Wunsch (y aún requiere  $O(nm)$  hora).

A medida que el algoritmo progresa, el  $F_{ij}$  será asignado para ser el puntaje óptimo para la alineación del primer  $i=0,\dotsc ,n$ personajes en A y el primero $j=0,\dotsc ,m$ personajes de B . El principio de optimización se aplica de la siguiente manera:

Base:

 $F_{0j}=d*j$ 
 $F_{i0}=d*i$ 

Recursión, basada en el principio de optimización:

 $F_{ij}=\max(F_{i-1,j-1}+S(A_{i},B_{j}),\;F_{i,j-1}+d,\;F_{i-1,j}+d)$ 

El pseudocódigo del algoritmo para calcular la matriz F se ve así:
d ← MismatchScore
 para i = 0 a la  longitud (A)
  F (i, 0) ← d * i
para j = 0 a la  longitud (B)
  F (0, j) ← d * j
para i = 1 a la  longitud (A)
   para j = 1 a la  longitud (B)
  {
    Match ← F (i-1, j-1) + S (A _i , B _j )
    Eliminar ← F (i-1, j) + d
    Insertar ← F (i, j-1) + d
    F (i, j) ← max (Emparejar, Insertar, Eliminar)
  }


Una vez que se calcula la matriz F , la entrada $F_{nm}$ da la puntuación máxima entre todas las alineaciones posibles. Para calcular una alineación que realmente proporciona esta puntuación, comience desde la celda inferior derecha y compare el valor con las tres fuentes posibles (Coincidencia, Insertar y Eliminar arriba) para ver de dónde proviene. Si coincide, entonces $A_{i}$  y  $B_{j}$  están alineados, si Eliminar, entonces  $A_{i}$  está alineado con un espacio, y si Insertar, entonces  $B_{j}$ está alineado con una brecha. (En general, más de una opción puede tener el mismo valor, lo que lleva a alineamientos óptimos alternativos).
AlineaciónA ← ""
AlineamientoB ← ""
i ← longitud (A)
j ← longitud (B)
 mientras que (i> 0 o j> 0)
{
  if (i> 0 y j> 0 y F (i, j) == F (i-1, j-1) + S (A _i , B _j ))
  {
    Alineación A ← A _i + Alineación A
    Alineamiento B ← B _j + Alineamiento B
    i ← i - 1
    j ← j - 1
  }
  más  si (i> 0 y F (i, j) == F (i-1, j) + d)
  {
    Alineación A ← A _i + Alineación A
    Alineamiento B ← "-" + Alineamiento B
    i ← i - 1
  }
  más
  {
    AlineaciónA ← "-" + AlineaciónA
    Alineamiento B ← B_j + Alineamiento 
    j ← j - 1
  }
}


Complejidad [ editar ]

Calcular el puntaje  $F_{ij}$  para cada celda en la tabla es un  $O(1)$ operación. Así, la complejidad temporal del algoritmo para dos secuencias de longitud y  es  $O(mn)$ . ^[3] Se ha demostrado que es posible mejorar el tiempo de ejecución para $O(mn/\log n)$ utilizando el método de los cuatro rusos . ^[3]^[4] Dado que el algoritmo llena un $n\times m$  tabla de la complejidad del espacio es  $O(mn)$ . ^[3]

Notas históricas y desarrollo de algoritmos [ editar ]

El propósito original del algoritmo descrito por Needleman y Wunsch era encontrar similitudes en las secuencias de aminoácidos de dos proteínas.^[1]

Needleman y Wunsch describen su algoritmo explícitamente para el caso en que la alineación se penaliza únicamente por las coincidencias y los desajustes, y los huecos no tienen penalización ( d = 0). La publicación original de 1970 sugiere la recurrencia.  $F_{ij}=\max _{h<i,k<j}\{F_{h,j-1}+S(A_{i},B_{j}),F_{i-1,k}+S(A_{i},B_{j})\}$ .

El algoritmo de programación dinámica correspondiente lleva tiempo cúbico. El documento también señala que la recursión puede acomodar fórmulas arbitrarias de penalización de brechas:


Un factor de penalización, un número restado por cada brecha realizada, puede evaluarse como una barrera para permitir la brecha. El factor de penalización podría ser una función del tamaño y / o dirección de la brecha. [página 444]


David Sankoff introdujo por primera vez un mejor algoritmo de programación dinámica con tiempo de ejecución cuadrático para el mismo problema (sin penalización por hueco) ^[5] . En 1972, TK Vintsyuk descubrió algoritmos de tiempo cuadrático similares ^[6] para el procesamiento del habla ( "deformación del tiempo" ), y por Robert A. Wagner y Michael J. Fischer^[7] en 1974 para la coincidencia de cadenas.

Needleman y Wunsch formularon su problema en términos de maximizar la similitud. Otra posibilidad es minimizar la distancia de edición entre secuencias, presentada por Vladimir Levenshtein . Peter H. Sellers mostró ^[8] en 1974 que los dos problemas son equivalentes.

El algoritmo Needleman-Wunsch todavía se usa ampliamente para un óptimo alineación global , particularmente cuando la calidad de la alineación global es de suma importancia. Sin embargo, el algoritmo es costoso con respecto al tiempo y al espacio, proporcional al producto de la longitud de dos secuencias y, por lo tanto, no es adecuado para secuencias largas.

El desarrollo reciente se ha centrado en mejorar el costo de tiempo y espacio del algoritmo mientras se mantiene la calidad. Por ejemplo, en 2013, un algoritmo de alineación de secuencia global óptima y rápida (FOGSAA), ^[9] sugirió la alineación de secuencias de nucleótidos / proteínas más rápido que otros métodos de alineación global óptimos, incluido el algoritmo Needleman-Wunsch. El documento afirma que, en comparación con el algoritmo Needleman-Wunsch, FOGSAA logra una ganancia de tiempo del 70-90% para secuencias de nucleótidos muy similares (con> 80% de similitud), y 54-70% para secuencias que tienen 30-80% de similitud.