Bioestadística Clínica

Estimación de parámetros

En general, de las variables experimentales u observacionales no conocemos la fpd. Podemos conocer la familia (normal, binomial,...) pero no los parámetros. Para calcularlos necesitaríamos tener todos los posibles valores de la variable, lo que no suele ser posible.
La inferencia estadística trata de cómo obtener información (inferir) sobre los parámetros a partir de subconjuntos de valores (muestras) de la variable.

Estadístico: variable aleatoria que sólo depende de la muestra aleatoria elegida para calcularla.
Estimación: Proceso por el que se trata de averiguar un parámetro de la población representado, en general, por q a partir del valor de un estadístico llamado estimador y representado por 
El problema se resuelve en base al conocimiento de la "distribución muestral" del estadístico que se use.
¿Qué es esto? Concretemos, p.e. en la media (m). Si para cada muestra posible calculamos la media muestral () obtenemos un valor distinto ( es un estadístico: es una variable aleatoria y sólo depende de la muestra), habrá por tanto una fpd para , llamada distribución muestral de medias. La desviación típica de esta distribución se denomina error típico de la media. Evidentemente, habrá una distribución muestral para cada estadístico, no sólo para la media, y en consecuencia un error típico para cada estadístico.
Si la distribución muestral de un estadístico estuviera relacionada con algún parámetro de interés, ese estadístico podría ser un estimador del parámetro.

Los parámetros son medidas descriptivas de toda una población. Sin embargo, sus valores por lo general se desconocen, porque es poco factible medir una población entera. Por eso, usted puede tomar una muestra aleatoria de la población para obtener estimaciones de los parámetros. Un objetivo del análisis estadístico es obtener estimaciones de los parámetros de la población, junto con la cantidad de error asociada con estas estimaciones. Estas estimaciones se conocen también como estadísticos de muestra. Una línea de distribución ajustada es una curva que se basa en las estimaciones de los parámetros en lugar de los valores reales de los parámetros.

Existen diferentes tipos de estimaciones de parámetros:

• Las estimaciones de punto son el valor individual más probable de un parámetro. Por ejemplo, la estimación de punto de la media de la población (el parámetro) es la media de la muestra (la estimación del parámetro).
• Los intervalos de confianza son un rango de valores que probablemente contienen el parámetro de población.

Como un ejemplo de estimaciones de parámetros, supongamos que usted trabaja para un fabricante de bujías que está estudiando un problema en la separación de electrodos de sus bujías. Sería demasiado costoso medir cada bujía que se produce. En lugar de ello, usted toma una muestra aleatoria de 100 bujías y mide la separación de electrodos en milímetros. La media de la muestra es de 9.2. Esta es la estimación de punto para la media de la población (μ), y le informa que el valor más probable de la separación promedio para todas las bujías es 9.2. Usted también crea un intervalo de confianza de 95% para μ que es (8.8, 9.6). Esto significa que puede estar 95% seguro de que es el valor real de la separación promedio para todas las bujías están entre 8.8 y 9.6.

Podemos tomar una muestra, calcular en ella un estadístico (promedio o porcentaje, por ejemplo) y luego hacer afirmaciones respecto del correspondiente parámetro. Esto se conoce con el nombre de estimación de parámetros, y se puede hacer de dos formas:

• Estimación puntual: consiste en asumir que el parámetro tiene el mismo valor que el estadístico en la muestra.
• Estimación por intervalos: se asigna al parámetro un conjunto de posibles valores que están comprendidos en un intervalo asociado a una cierta probabilidad de ocurrencia. También se llaman “intervalos de confianza” debido a que la probabilidad asociada a ellos es la confianza de los mismos. Así, diremos que un intervalo de 99% de confianza es más confiable que uno de 95%. También se define la confianza de la estimación como la probabilidad de acertar con el intervalo.

La estimación que tiene valor estadístico para promedio o media y para el porcentaje de la población es esta última, que explicaremos a continuación.

Estimación de la media de la población

Explicaremos este punto con el siguiente ejemplo: queremos estimar el número de hijos promedio que tienen las mujeres de una población determinada. Con este objeto se seleccionó, por muestreo aleatorio simple, una muestra de 20 mujeres a quienes se entrevistó, obteniendo como resultado un promedio de 3,2 hijos y una desviación estándar de 0,8. Con estos resultados podríamos hacer una estimación puntual y decir que la población de interés tiene en promedio 3,2 hijos. Pero esta estimación tiene el inconveniente de que se desconoce el error que se está cometiendo.

Si a esta estimación le asignamos un error, que llamaremos E, podríamos decir que el promedio de hijos de la población está ubicado dentro de un intervalo de estimación que tiene como límite inferior 3,2 - E y como límite superior 3,2 + E. De este modo, le asignamos al resultado un intervalo de estimación. Si además le damos a este intervalo una probabilidad de ocurrencia de los valores comprendidos en él, habremos construido un intervalo de confianza para el promedio de hijos de nuestra población de mujeres.

Entonces, generalizando lo que se explicó para la variable “promedio de hijos”, podemos decir que:

Un intervalo de confianza para estimar el promedio de la población está constituido por los siguientes elementos: el promedio de la muestra y el error de estimación.

El elemento esencial en la construcción del intervalo de estimación es el error.

¿Cómo se obtiene el error en la construcción de un intervalo para el promedio?
Desarrollando la fórmula siguiente:

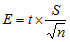Está compuesta por la desviación estándar de la muestra (S), el tamaño de la muestra (n) y, aquí aparece un elemento nuevo, t –Student-, que corresponde a una distribución de probabilidad muy similar a la distribución normal.

En la tabla de t los valores se buscan en función de dos cosas:

• la probabilidad que hemos elegido para nuestro intervalo, y
• los “grados de libertad” que se calculan restando 1 al tamaño de la muestra (n).

En nuestro ejemplo elegimos una confianza de 95% que, asociada a los 19 grados de libertad (n-1), nos conduce a un valor de tabla t de Student igual a 2,093. Ya veremos en forma detallada el uso práctico de la tabla t, recordemos por ahora el valor de “t” encontrado porque lo utilizaremos para la construcción del intervalo.

Volviendo a la fórmula para calcular el error, vemos entonces que el error está compuesto por tres elementos:

• El valor t que se obtiene de la tabla t de Student.
• La desviación estándar de la muestra.
• El tamaño de la muestra.

Volviendo a nuestro ejemplo, calculemos el error. Recordemos que deseamos conocer el número promedio de hijos que tienen las mujeres en esa población y que, estudiando una muestra de 20 mujeres, el resultado fue un promedio de 3,2 hijos y una desviación estándar de 0,8.

¿Cuáles son, entonces, los elementos que nos permitirán calcular el error de nuestra estimación?

El valor t que obtuvimos de la tabla t de Student	t = 2,093
La desviación estándar de la muestra	S = 0,8
El tamaño de la muestra	n = 20

Reemplazando esos valores en la fórmula obtendremos el error, que es:

Intervalo de estimación

Construiremos ahora el intervalo de estimación, sumando y restando al promedio, el error. De esta manera el límite inferior será: promedio - E; y el límite superior: promedio + E.

Límite inferior (a) = 3,2 - 0,37 = 2,83
Límite superior (b) = 3,2 + 0,37 = 3,57 

De este modo se consigue un intervalo (2,83; 3,57) que nos permite estimar, con 95% de confianza, que el promedio de hijos en la población de mujeres está entre 2,83 y 3,57.

En resumen, los pasos en la construcción de un intervalo de confianza para la estimación del promedio son:

• Obtener una muestra aleatoria.
• Calcular promedio y desviación estándar muestral.
• Elegir la confianza del intervalo (95% ó 99%).
• Obtener el valor de t en tabla.
• Calcular el error de estimación.
• Calcular los límites del intervalo (a y b).

De estos 6 puntos, ya hemos tratado los puntos 1, 2, 5 y 6.

Sólo haremos un comentario sobre el punto 3: la elección de la confianza. Lo decide el investigador y se podría elegir cualquier valor, pero por lo general se usa 95% ó 99%. La elección de uno u otro dependerá de la confianza y la precisión que necesitemos para nuestra estimación, ya que si el intervalo es más grande, la precisión será menor; por lo tanto, un intervalo de 99% tiene mayor confianza y menor precisión que uno de 95%.

Distribución muestral de medias Si tenemos una muestra aleatoria de una población N(m,s ), se sabe (Teorema del límite central) que la fdp de la media muestral es también normal con media m y varianza s2/n. Esto es exacto para poblaciones normales y aproximado (buena aproximación con n>30) para poblaciones cualesquiera. Es decir es el error típico, o error estándar de la media. ¿Cómo usamos esto en nuestro problema de estimación? 1º problema: No hay tablas para cualquier normal, sólo para la normal m=0 y s=1 (la llamada z); pero haciendo la transformación (llamada tipificación) una normal de media m y desviación s se transforma en una z. Llamando za al valor de una variable normal tipificada que deja a su derecha un área bajo la curva de a, es decir, que la probabilidad que la variable sea mayor que ese valor es a (estos son los valores que ofrece la tabla de la normal) podremos construir intervalos de la forma para los que la probabilidad es 1 - a. Teniendo en cuenta la simetría de la normal y manipulando algebraícamente que también se puede escribir o, haciendo énfasis en que es el error estándar de la media, Recuérdese que la probabilidad de que m esté en este intervalo es 1 - a. A un intervalo de este tipo se le denomina intervalo de confianza con un nivel de confianza del 100(1 - a)%, o nivel de significación de 100a%. El nivel de confianza habitual es el 95%, en cuyo caso a=0,05 y za /2=1,96. Al valor se le denomina estimación puntual y se dice que es un estimador de m. Ejemplo: Si de una población normal con varianza 4 se extrae una muestra aleatoria de tamaño 20 en la que se calcula se puede decir que m tiene una probabilidad de 0,95 de estar comprendida en el intervalo que sería el intervalo de confianza al 95% para m En general esto es poco útil, en los casos en que no se conoce m tampoco suele conocerse s2; en el caso más realista de s2 desconocida los intervalos de confianza se construyen con la t de Student (otra fdp continua para la que hay tablas) en lugar de la z. o, haciendo énfasis en que es el error estándar estimado de la media, Este manera de construir los intervalos de confianza sólo es válido si la variable es normal. Cuando n es grande (>30) se puede sustituir t por z sin mucho error. http://www.hrc.es/bioest/esti_medias.html