Bioestadística Clínica

Estimación de proporciones Sea X una variable binomial de parámetros n y p (una variable binomial es el número de éxitos en n ensayos; en cada ensayo la probabilidad de éxito (p) es la misma, por ejemplo: número de diabéticos en 2000 personas). Si n es grande y p no está próximo a 0 ó 1 (np ³ 5) X es aproximadamente normal con media np y varianza npq (siendo q = 1 - p) y se puede usar el estadístico (proporción muestral), que es también aproximadamente normal, con error típico dado por  en consecuencia, un IC para p al 100(1 - a)% será es decir, la misma estructura que antes:  Obsérvese que para construirlo, ¡se necesita conocer p!. Si n es grande (>30) se pueden substituir p y q por sus estimadores sin mucho error, en cualquier caso como pq £ 0,25 si se substituye pq por 0,25 se obtiene un intervalo más conservador (más grande). Ejemplo: En una muestra de 100 pacientes sometidos a un cierto tratamiento se obtienen 80 curaciones. Calcular el intervalo de confianza al 95% de la eficacia del tratamiento. ¿Qué significa este intervalo? La verdadera proporción de curaciones está comprendida entre, aproximadamente, 72% y 88% con un 95% de probabilidad.  ESTIMACIÓN DE UNA PROPORCIÓN INTRODUCCIÓN Como recordarás, la distribución binomial B(n,p), nos permite conocer como se distribuye el número de éxitos, correspondiente a un experimento realizado n veces, y en el que la probabilidad de éxito en cada experimento es p. Dicha distribución tiene media y desviación típica: Supongamos que sea X la variable que mide el número de éxitos. Ya sabes que los posibles valores de X son  0,1,2,...,n. Si utilizaramos la nueva variable, ésta tomaría los valores correspondientes a las proporciones (en tanto por uno) de éxito. Si por ejemplo n=200, se tendría: X=0 , (0 éxitos ) equivale a Y=0 ( es decir un 0% de éxitos) X=1 , (1 éxito ) equivale a Y=0,005 ( es decir 0,5% de éxitos) X=2 , Y=0,01 ( es decir 2 éxitos equivalen a un 1% de éxitos) .... X=n  , Y=1 ( n éxitos = 100% de éxitos) Dividiendo por n, obtendremos la media y desviación típica de la variable Y que representa la proporción de éxitos:        Si ademásnp>5, nq>5, utilizando la aproximación normal a la binomial,podremos afirmar que las proporciones de éxito para un experimento binomial de n pruebas con probabilidad de éxito p en cada prueba, se distribuyen según: DISTRIBUCIÓN MUESTRAL DE PROPORCIONES Imaginemos que sabemos que la proporción del alumnado de nuestro centro que es favorable a realizar una huelga es del 60%. Cuando elegimos a un alumno, y nos preguntamos si es favorable a la huelga, es como si realizaramos una prueba binomial con probabilidad de éxito p=0,6. Cuando elijamos muestras aleatorias de digamos 70 alumnos, el número de ellos favorable a la huelga, deberá seguir una distribución B(70, 0´6), o bien, la proporción de ellos que es favorablese debe distribuir según ( Debe notarse que en este caso,  n=70, p=0,6, q=0,4 y por tanto np>5, nq>5), o lo que es lo mismo, las proporciones que vayamos encontrando para muestras de tamaño 70, se iran distribuyendo de forma "normal" alrededor del 60%, con una desviaición típica del 5,8%. Por tanto, si en una población, una determinada característica de tipo binomial (es decir la población se divide entre los que la tienen y los que no), se presenta en una proporción p, al tomar muestras de tamaño n, las proporciones p' obtenidas, se distribuirán según (a partir de este momento supondremos siempre que np>5,nq>5). A esta distribución se la denomina distribución muestral de proporciones. Resultará muy interesante que hagas las actividades de la hoja de cálculo Distribución Muestral de Proporciones EJEMPLO: En una empresa está establecido que si una máquina opera correctamente, como máximo un 5% de su producción es defectuosa. Si se elige aleatoriamente una muestra de 40 artículos producidos por una máquina y 15 de ellos son defectuosos, ¿existe razón para pensar que la máquina está averiada?. Las proporciones muestrales para muestras de tamaño 40 en una máquina normal se distribuyen según , es decir se distribuyen de forma "normal" alrededor del 5% con una d.t. del 3'4%. En consecuencia, la probabilidad de valores como el registrado resulta ser: y podemos asegurar "estadísticamente" que la máquina está averiada. Ahora que sabemos como se distribuyen las proporciones muestrales, por un proceso similar al utilizado para estimar la media poblacional, podremos realizar estimaciones sobre la proporción poblacional de un carácter, conociendo la proporción en una muestra. ESTIMACIÓN DE UNA PROPORCIÓN Imaginemos que hemos tomado una muestra aleatoria de 500 personas, y que les preguntamos si creen que el Presidente del Gobierno debe dimitir, obteniendo el SÍ un 70%. Supongamos que nos planteamos un intervalo de confianza del 90% para poder estimar el porcentaje  p de toda la población que diría SÍ Según todo lo dicho, las proporciones del SÍ en las muestras, se distribuirán según: Como quiera que no conocemos la verdadera proporción p, no podemos conocer la desviación típica de la distribución muestral por lo que utilizaremos como sustituto para p, la proporción muestral p'=0,7, que causará poco cambio en los resultados finales. 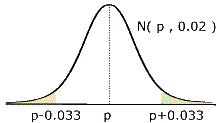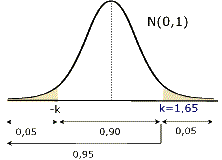En consecuencia, las proporciones muestrales, siguen la distribución N(p,0,02)  (Nota: puesto que utilizamos tantos por uno, deberemos utilizar en los cálculos una precisión de al menos centésimas, mejorando el resultado si precisamos más) Llevando a cabo los mismos pasos que en el caso de la estimación de medias, vemos que un 90% de las proporciones muestrales que se obtengan estarán a como máximo 1,65 desviaciones típicas de p (es decir a ) ,  y en consecuencia, si suponemos que p' es una de tales proporciones ( y será acertado suponerlo en un 90% de los casos ), la verdadera proporción quedará siempre en el intervalo (p'-0'033 , p'+0'033)=(0'667,0'733). Esto lo podemos expresar como: "Con un nivel de confianza del 90%, la proporción de españoles que creen que el Presidente del Gobierno debe dimitir es de un 70%, con un  error máximo de ± 3,3 % " Para entender mejor el proceso, observa el gráfico interactivo en el que se supone que la verdadera proporción es p=0.72 Comenzamos con el valor k=1.65, que corresponde a una confianza del 90%. Luego hallamos el área roja, que corresponde a las proporciones muestrales que tienen una probabilidad de aparición del 90%. Si la proporción muestral (p´) obtenida es, como en el caso que nos ocupa, p´=0.7 , puedes comprobar como el intervalo de confianza contiene a la verdadera proporción. Varía el nivel  de confianza, y anota que le ocurre al intervalo de confianza. Así mismo, puedes variar el valor de la proporción muestral, e investigar, qué valores dan lugar a intervalos que no contienen a la media de la población y cuál es la probabilidad de ocurrencia de dichos valores.  TAMAÑO DE LA MUESTRA Como ya sabemos, el error máximo depende del tamaño de la muestra: a muestras mayores corresponden errores menores. Normalmente, cuando queremos hacer una estimación, con un determinado margen de confianza, nos plantearemos que el error máximo tenga un determinado valor. Imaginemos por ejemplo que queremos conocer el porcentaje de alumnos de nuestro centro , que es favorable a hacer la Fuga de San Diego el día 12 de Noviembre (este carácter se considerará como éxito) en contraposición con los que la quieren  hacer en otra fecha. Nos marcamos un nivel de confianza del 90%, y queremos que el error máximo no sobrepase el 10%. Puesto que el error máximo es ,  el tamaño de la muestra habrá de ser Existe un problema: no conocemos p, ni tan siquiera el valor p' de la muestra puesto que aún no ha sido realizada la encuesta (a no ser que por anteriores sondeos, pueda tenerse un valor fiable para p). Si se tiene información previa sobre el valor de p, puede utilizarse, pero si no, se utilizará inicialmente p=0,5, pues se puede demostrar que para este valor se obtiene el máximo valor del tamaño de la muestra ( mirar grafico siguiente) y en consecuencia, quedará asegurado que el error es como máximo del 10% En este caso concreto, tomando E=0,1  , p=0,5 , k=1,65, obtendremos que n=68,08»69 es el tamaño de la muestra que debemos tomar. Aunque el error máximo fijado es del 10%, en la práctica resultará en general más pequeño, a medida que la verdadera proporción p se aleje del valor 0,5. En particular, si en lugar de tomar inicialmente p=0,5 , hubieramos supuesto que p=0,95   , el error  máximo que cometeríamos utilizando 68 personas en la muestra sería: E= 0,043, es decir un 4,3%. Una vez estimado p, podremos reajustar el margen de error cometido. En la práctica normalmente no dispondremos de información previa sobre el valor de p, y deberemos partir  de p=0,5  , tal y como verás que se explicita en la ficha técnica de los estudios que se publican. El grafico de la izquierda nos permitirá analizar numéricamente el valor de E. Observa como varía el error para p=0,5 y para el resto de valores de p y comprueba lo argumentado en los párrafos anteriores EJEMPLO 1: Utiliza el gráfico anterior para comentar numéricamente las frases: "Se obtiene más información (en términos de error) de una muestra de 1000 personas de un colectivo de 100.000.000 , que de 50 de un colectivo de 250". "Si queremos aumentar  la confianza en una estimación por intervalo, deberemos manejar un mayor margen de error" EJEMPLO 2: Imagina que queremos estimar con un error máximo del 3%, el porcentaje de audiencia de un programa de TV, y queremos un 95% de confianza para nuestros resultados. No disponemos de información previa sobre el posible valor de p. ¿Cuántos telespectadoeres deberán ser encuestados? Para un nivel de confianza del 95%  deberemos tomar  k=1,96. Puesto que desconocemos p , tomaremos p=0,5, con lo que   n=1068 (redondeado). Tenemos pues un 95% de confianza en que el porcentaje que encontremos se halle a menos de tres puntos porcentuales de la proporción exacta.Teniendo en cuenta que este número de telespectadores es muy pequeño respecto del total de telespectadores, nos daremos cuenta de la potencia del método de estimación. Utiliza el gráfico anterior para tomando los valores de k y n, comprobar los resultados del ejercicio. https://www.matematicasonline.es/BachilleratoCCSS/segundo/archivos/Inferencia_estadistica/estimacion_de_una_proporcion.htm