FORMAS GEOMÉTRICAS - SUPERFICIES

 superficie catalana , llamada así por el matemático belga Eugène Charles Catalan , es una superficie reglada cuyas reglas son paralelas a un plano fijo .

Una superficie catalana.

Ecuaciones [ editar ]

La ecuación vectorial de una superficie catalana está dada por

r = s ( u ) + v L ( u ),

donde r = s ( u ) es la curva de espacio y L ( u ) es el vector unitario de la regla en u = u . Todos los vectores L ( u) son paralelos al mismo plano, denominado plano directriz de la superficie. Esto se puede caracterizar por la condición: el producto mixto [ L ( u ), L ' ( u ), L " ( u )] = 0. [1]

Las ecuaciones paramétricas de la superficie catalana son [2].

$${\ displaystyle x = f (u) + vi (u), \ quad y = g (u) + vj (u), \ quad z = h (u) + vk (u) \,}

Casos especiales [ editar ]

Si todas las reglas de una superficie catalana se intersecan con una línea fija , entonces la superficie se llama conoide .

El catalán demostró que el helicoide y el avión eran las únicas superficies mínimas gobernadas .

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Superficie del canal: Directrix es una hélice , con sus esferas generadoras.

Superficie de la tubería: Directrix es una hélice, con esferas generadoras.

Superficie de la tubería: Directrix es una hélice.

Una superficie de canal o canal es una superficie formada como la envoltura de una familia de esferas cuyos centros se encuentran en una curva espacial, su directriz . Si los radios de las esferas generadoras son constantes, la superficie del canal se llama superficie de la tubería . Ejemplos simples son:

• cilindro circular derecho (superficie de la tubería, directriz es una línea, el eje del cilindro)
• toro (superficie de la tubería, directriz es un círculo),
• cono circular derecho (superficie del canal, directriz es una línea (el eje), radios de las esferas no constantes),
• superficie de revolución (superficie del canal, directriz es una línea),

Las superficies de los canales desempeñan un papel esencial en la geometría descriptiva, porque en el caso de una proyección ortográfica, su curva de contorno se puede dibujar como la envolvente de los círculos.

• En el área técnica, las superficies de los canales se pueden utilizar para mezclar superficies sin problemas.

Sobre de un lápiz de superficies implícitas [ editar ]

Dado el lápiz de superficies implícitas.

$${\ displaystyle \ Phi _ {c}: f ({\ mathbf {x}}, c) = 0, c \ en [c_ {1}, c_ {2}]}.

Dos superficies vecinas $${\ displaystyle \ Phi _ {c}} y $${\ displaystyle \ Phi _ {c + \ Delta c}} Se intersecan en una curva que cumple las ecuaciones.

$${\ displaystyle f ({\ mathbf {x}}, c) = 0} y $${\ displaystyle f ({\ mathbf {x}}, c + \ Delta c) = 0}.

Para el limite $${\ displaystyle \ Delta c \ to 0} uno obtiene $${\ displaystyle f_ {c} ({\ mathbf {x}}, c) = \ lim _ {\ Delta \ to \ 0} {\ frac {f ({\ mathbf {x}}, c) -f ({ \ mathbf {x}}, c + \ Delta c)} {\ Delta c}} = 0}. La última ecuación es la razón de la siguiente definición.

• Permitir $${\ displaystyle \ Phi _ {c}: f ({\ mathbf {x}}, c) = 0, c \ en [c_ {1}, c_ {2}]} Un lápiz de 1 parámetro de regular implícito. $${\ displaystyle C ^ {2}} - superficies ($${\ displaystyle f}es al menos dos veces continuamente diferenciable). La superficie definida por las dos ecuaciones.

  $${\ displaystyle f ({\ mathbf {x}}, c) = 0, \ quad f_ {c} ({\ mathbf {x}}, c) = 0}

Es el sobre del lápiz de superficies dado. ^[1]

Superficie Canal [ editar ]

Permitir $${\ displaystyle \ Gamma: {\ mathbf {x}} = {\ mathbf {c}} (u) = (a (u), b (u), c (u)) ^ {\ top}} una curva de espacio regular y $${\ displaystyle r (t)} una $${\ displaystyle C ^ {1}} -función con {\ displaystyle r> 0} y {\ displaystyle | {\ dot {r}} | <\ | {\ dot {\ mathbf {c}}} \ |}. La última condición significa que la curvatura de la curva es menor que la de la esfera correspondiente.

El sobre del lápiz de 1 parámetro de esferas.

$${\ displaystyle f ({\ mathbf {x}}; u): = {\ big (} {\ mathbf {x}} - {\ mathbf {c}} (u) {\ big)} ^ {2} - r (u) ^ {2} = 0}

se llama superficie del canal y$${\ displaystyle \ Gamma}Su directriz . Si los radios son constantes, se llama superficie de tubería .

Representación paramétrica de una superficie del canal [ editar ]

La condición del sobre

$${\ displaystyle f_ {u} ({\ mathbf {x}}, u): = 2 {\ Big (} {\ big (} {\ mathbf {x}} - {\ mathbf {c}} (u) { \ big)} {\ dot {\ mathbf {c}}} (u) -r (u) {\ dot {r}} (u) {\ Big)} = 0},

de la superficie del canal de arriba es para cualquier valor de $${\ displaystyle u} La ecuación de un plano, que es ortogonal a la tangente. $${\ displaystyle {\ dot {\ mathbf {c}}} (u)}de la directriz. De ahí que el sobre sea una colección de círculos. Esta propiedad es la clave para una representación paramétrica de la superficie del canal. El centro del círculo (para parámetro$${\ displaystyle u}) tiene la distancia {\ displaystyle d: = {\ frac {r {\ dot {r}}} {\ | {\ dot {\ mathbf {c}}} \ |}}  (s. condición arriba) desde el centro de la esfera correspondiente y su radio es $${\ displaystyle {\ sqrt {r ^ {2} -d ^ {2}}}}. Por lo tanto

• $${\ displaystyle {\ mathbf {x}} = {\ mathbf {x}} (u, v): = {\ mathbf {c}} (u) - {\ frac {r (u) {\ dot {r} } (u)} {\ | {\ dot {\ mathbf {c}}} (u) \ | ^ {2}}} {\ dot {\ mathbf {c}}} (u) + {\ frac {r (u) {\ sqrt {\ | {\ dot {\ mathbf {c}}} (u) \ | ^ {2} - {\ dot {r}} ^ {2}}}} {\ | {\ dot {\ mathbf {c}}} (u) \ |}} {\ big (} {\ mathbf {e}} _ {1} (u) \ cos (v) + {\ mathbf {e}} _ {2 } (u) \ sin (v) {\ big)},}

donde los vectores $${\ displaystyle {\ mathbf {e}} _ {1}, {\ mathbf {e}} _ {2}} y el vector tangente $${\ displaystyle {\ dot {\ mathbf {c}}}}forman una base ortonormal, es una representación paramétrica de la superficie del canal. ^[2]

por $${\ displaystyle {\ dot {r}} = 0}uno obtiene la representación paramétrica de una superficie de tubería :

• $${\ displaystyle {\ mathbf {x}} = {\ mathbf {x}} (u, v): = {\ mathbf {c}} (u) + r {\ big (} {\ mathbf {e}} _ {1} (u) \ cos (v) + {\ mathbf {e}} _ {2} (u) \ sin (v) {\ big)}.}

nudo de tubo

superficie del canal: ciclismo Dupin

Ejemplos [ editar ]

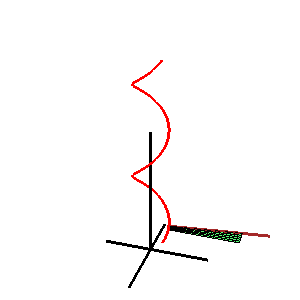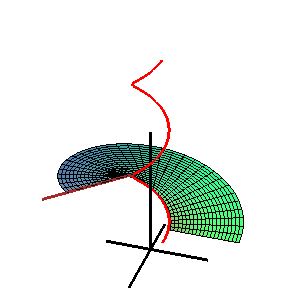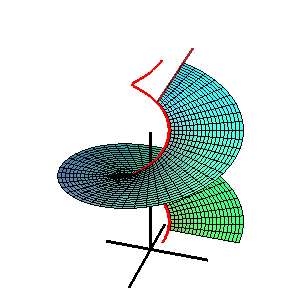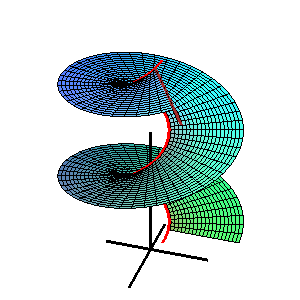
a) La primera imagen muestra una superficie del canal con

1. la hélice $${\ displaystyle (\ cos (u), \ sin (u), 0.25u), u \ en [0,4]}como directriz y
2. la función de radio $${\ displaystyle r (u): = 0.2 + 0.8u / 2 \ pi}.
3. La elección para $${\ displaystyle {\ mathbf {e}} _ {1}, {\ mathbf {e}} _ {2}} es el siguiente:

$${\ displaystyle {\ mathbf {e}} _ {1}: = ({\ dot {b}}, - {\ dot {a}}, 0) / \ | \ cdots \ |, \ {\ mathbf {e }} _ {2}: = ({\ mathbf {e}} _ {1} \ times {\ dot {\ mathbf {c}}}) / \ | \ cdots \ |}.

b) Para la segunda imagen el radio es constante:$${\ displaystyle r (u): = 0.2}, es decir, la superficie del canal es una superficie de tubería.

c) Para la imagen 3. la superficie de la tubería b) tiene parámetro $${\ displaystyle u \ en [0,7.5]}.

d) La imagen 4. muestra un nudo de tubo. Su directriz es una curva sobre un toro.

e) La imagen 5. muestra un ciclón Dupin (superficie del canal).

superficie circular es la imagen de un mapa ƒ  :  I ×  S ¹  →  R ³ , donde I  ⊂  R es un intervalo abierto y S ¹ es el círculo unidad , definido por

$${\ displaystyle f (t, \ theta): = \ gamma (t) + r (t) {\ mathbf {u}} (t) \ cos \ theta + r (t) {\ mathbf {v}} (t ) \ sin \ theta, \,}

donde γ, u , v  : I → R ³ y r  :  I  rightarrow  R _{> 0} , cuando R _{> 0}  : = { x ∈ R  : x > 0}. Además, generalmente se asume que u · u =  v · v = 1 y u · v = 0, donde punto denota el producto escalar canónico en R ³ , es decir, u y vson longitudes de unidad y mutuamente perpendiculares. El mapa γ:  I  →  R ³ se denomina curva base para la superficie circular y los dos mapas u ,  v  :  I  →  R ³ se denominan el cuadro de dirección de la superficie circular. Para un t ₀  ∈  fijo , la imagen de ƒ ( t ₀ ,  θ ) se denomina círculo generador de la superficie circular. ^[1]

Las superficies circulares son un análogo de las superficies regladas . En el caso de superficies circulares los generadores son círculos; Llama a los círculos generadores. En el caso de la superficie reglada, los generadores son líneas rectas; llamados dictámenes.