LISTA DE TEMAS MATEMÁTICOS - ÁLGEBRA ABSTRACTA

En álgebra abstracta , un grupo abeliano ( G , +) se llama finitamente generado si existen finamente muchos elementos x ₁ , ..., x _s en G , de manera que cada x en G se puede escribir en la forma

x = n ₁ x ₁ + n ₂ x ₂ + ... + n _s x _s

con enteros n ₁ , ..., n _s . En este caso, se dice que el conjunto { x ₁ , ..., x _s } es un grupo electrógeno de G o que x ₁ , ..., x _s generar G .

Cada grupo abeliano finito es generado finamente. Los grupos abelianos finamente generados pueden ser clasificados completamente.

Ejemplos [ editar ]

• Los enteros ,$${\ displaystyle \ left (\ mathbb {Z}, + \ right)}, son un grupo abeliano finamente generado.
• Los enteros modulo$${\ displaystyle n}, $${\ displaystyle \ left (\ mathbb {Z} / n \ mathbb {Z}, + \ right)}, son un grupo abeliano finito (por lo tanto, generado finamente).
• Cualquier suma directa de muchos grupos abelianos finamente generados es de nuevo un grupo abeliano finamente generado.
• Cada celosía forma un grupo abeliano libre finamente generado .

No hay otros ejemplos (hasta isomorfismo). En particular, el grupo.$${\ displaystyle \ left (\ mathbb {Q}, + \ right)}de números racionales no se genera de forma finita: ^[1] si$${\ displaystyle x_ {1}, \ ldots, x_ {n}}Son números racionales, escoge un número natural. $${\ displaystyle k} coprime a todos los denominadores; entonces$${\ displaystyle 1 / k} no puede ser generado por $${\ displaystyle x_ {1}, \ ldots, x_ {n}}. El grupo$${\ displaystyle \ left (\ mathbb {Q} ^ {*}, \ cdot \ right)}de números racionales distintos de cero tampoco se genera de forma definitiva. Los grupos de números reales bajo suma.$${\ displaystyle \ left (\ mathbb {R}, + \ right)} y números reales distintos de cero bajo multiplicación $${\ displaystyle \ left (\ mathbb {R} ^ {*}, \ cdot \ right)}Tampoco se generan finamente. ^[1] [2]

Clasificación [ editar ]

El teorema fundamental de los grupos abelianos finamente generados se puede exponer de dos maneras, generalizando las dos formas del teorema fundamental de los grupos abelianos finitos . El teorema, en ambas formas, a su vez generaliza el teorema de la estructura para módulos generados de manera finita sobre un dominio ideal principal , que a su vez admite otras generalizaciones.

Descomposición primaria [ editar ]

La formulación de descomposición primaria establece que cada grupo abeliano G finamente generado es isomorfo a una suma directa de grupos cíclicos primarios y grupos cíclicos infinitos . Un grupo cíclico primario es aquel cuyo orden es una potencia de un primo . Es decir, cada grupo abeliano finamente generado es isomorfo a un grupo de la forma

$${\ displaystyle \ mathbb {Z} ^ {n} \ oplus \ mathbb {Z} _ {q_ {1}} \ oplus \ cdots \ oplus \ mathbb {Z} _ {q_ {t}},}

donde n ≥ 0 es el rango , y los números q ₁ , ..., q _t son potencias de números primos (no necesariamente distintos). En particular, G es finito si y sólo si n = 0. Los valores de n , q ₁ , ..., q _t son ( hasta la reordenación de los índices) determinadas únicamente por G .

Factor de descomposición invariante [ editar ]

También podemos escribir cualquier grupo abeliano G finamente generado como una suma directa de la forma

$${\ displaystyle \ mathbb {Z} ^ {n} \ oplus \ mathbb {Z} _ {k_ {1}} \ oplus \ cdots \ oplus \ mathbb {Z} _ {k_ {u}},}

donde k ₁ divide k ₂ , que divide k ₃ y así sucesivamente hasta k _u . Nuevamente, el rango n y los factores invariantes k ₁ , ..., k _u están determinados únicamente por G (aquí con un orden único). El rango y la secuencia de factores invariantes determinan el grupo hasta el isomorfismo.

Equivalencia [ editar ]

Estas declaraciones son equivalentes como resultado del teorema del resto chino , lo que implica que$${\ displaystyle \ mathbb {Z} _ {jk} \ simeq \ mathbb {Z} _ {j} \ oplus \ mathbb {Z} _ {k}}si y solo si j y k son coprime .

Historia [ editar ]

La historia y el crédito para el teorema fundamental se complican por el hecho de que se demostró cuando la teoría de grupos no estaba bien establecida y, por lo tanto, las formas tempranas, aunque esencialmente el resultado y la prueba modernos, a menudo se presentan para un caso específico. Brevemente, una forma temprana del caso finito se probó en ( Gauss 1801 ), el caso finito se probó en ( Kronecker 1870 ) y se expresó en términos teóricos de grupo en ( Frobenius y Stickelberger 1878 ). El caso presentado finitamente se resuelve con la forma normal de Smith y, por lo tanto, se acredita con frecuencia a ( Smith 1861 ), ^[3] aunque a veces el caso generado de manera finita se acredita a (Poincaré 1900 ); Los detalles siguen.

El teórico del grupo László Fuchs afirma: ^[3]

En lo que respecta al teorema fundamental sobre los grupos abelianos finitos, no está claro qué tan atrás en el tiempo hay que ir para rastrear su origen. ... tomó mucho tiempo formular y probar el teorema fundamental en su forma actual ...

El teorema fundamental para los grupos abelianos finitos fue comprobado por Leopold Kronecker en ( Kronecker 1870 ), utilizando una prueba de la teoría de grupos ^[4], aunque sin enunciarlo en términos de la teoría de grupos; ^{[5] se} presenta una presentación moderna de la prueba de Kronecker en ( Stillwell 2012 ), 5.2.2 Teorema de Kronecker, 176–177 . Esto generalizó un resultado anterior de Carl Friedrich Gauss de Disquisitiones Arithmeticae (1801), que clasificó formas cuadráticas; Kronecker citó este resultado de Gauss. El teorema fue declarado y probado en el lenguaje de los grupos por Ferdinand Georg Frobenius yLudwig Stickelberger en 1878. ^[6] [7] Otra formulación teórica grupal fue dada por Eugen Netto , estudiante de Kronecker, en 1882. ^[8] [9]

Henry John Stephen Smith demostró el teorema fundamental para los grupos abelianos finamente presentadosen ( Smith 1861 ), ^[3] como matrices enteras que corresponden a presentaciones finitas de grupos abelianos (esto se generaliza a los módulos presentados finitamente sobre un dominio ideal principal), y Smith La forma normalcorresponde a la clasificación de grupos abelianos finamente presentados. Existe la tecnicidad adicional de demostrar que un grupo abeliano finamente presentado es de hecho finamente generado , por lo que la clasificación de Smith no es una prueba completa para grupos abelianos generados finamente.

Henri Poincaré ( Poincaré 1900 ) probó el teorema fundamental para los grupos abelianos generados de maneradefinitiva , utilizando una prueba de matriz (que se generaliza a los dominios ideales principales). Esto se hizo en el contexto de calcular la homología de un complejo, específicamente el número de Betti y los coeficientes de torsión de una dimensión del complejo, donde el número de Betti corresponde al rango de la parte libre, y los coeficientes de torsión corresponden a la parte de torsión . ^[4]

La prueba de Kronecker fue generalizada a grupos abelianos generados finamente por Emmy Noether en ( Noether 1926 ). ^[4]

Corolarios [ editar ]

Dicho de manera diferente, el teorema fundamental dice que un grupo abeliano finamente generado es la suma directa de un grupo abeliano libre de rango finito y un grupo abeliano finito, cada uno de los cuales es único hasta el isomorfismo. El grupo abeliano finito es sólo el subgrupo de torsión de G . El rango de G se define como el rango de la parte libre de torsión de G ; este es sólo el número n en las fórmulas anteriores.

Un corolario del teorema fundamental es que todo grupo abeliano sin torsión finamente generado es abeliano libre. La condición finamente generada es esencial aquí:$${\ displaystyle \ mathbb {Q}} Es libre de torsión pero no es abeliano libre.

Cada subgrupo y grupo de factores de un grupo abeliano finamente generado se genera de nuevo finamente abeliano. Los grupos abelianos finamente generados, junto con los homomorfismos de grupo , forman una categoría abeliana que es una subcategoría de Serre de la categoría de grupos abelianos .

Grupos abelianos no generados de forma definitiva [ editar ]

Tenga en cuenta que no todos los grupos abelianos de rango finito se generan de manera finita; el grupo de rango 1$${\ displaystyle \ mathbb {Q}}es un contraejemplo, y el grupo de rango 0 dado por una suma directa de infinitamente innumerablescopias de$${\ displaystyle \ mathbb {Z} _ {2}} es otro.

rango , rango Prüfer , o rango libre de torsión de un grupo abeliano A es la cardinalidadde un maximal linealmente independientes subconjunto. ^[1] El rango de A determina el tamaño de la más grande grupo abeliano libre contenida en A . Si A es libre de torsión entonces se incrusta en un espacio vectorial sobre los números racionales de rango dimensión A . Para grupos abelianos finamente generados.El rango es un invariante fuerte y cada grupo está determinado por isomorfismo por su subgrupo de rango y torsión . Grupos abelianos libres de torsión de rango 1 se han clasificado completamente. Sin embargo, la teoría de los grupos abelianos de rango más alto es más complicada.

El término rango tiene un significado diferente en el contexto de los grupos abelianos elementales .

Definición [ editar ]

Un subconjunto { a _α } de un grupo abeliano es linealmente independiente (sobre Z ) si la única combinación lineal de estos elementos que es igual a cero es trivial: si

$${\ displaystyle \ sum _ {\ alpha} n _ {\ alpha} a _ {\ alpha} = 0, \ quad n _ {\ alpha} \ in \ mathbb {Z},}

donde todos pero un número finito de coeficientes n _α son cero (de modo que la suma es, en efecto, finito), entonces todos los sumandos son 0. Cualquier dos máximos conjuntos linealmente independientes en A tienen la misma cardinalidad , que se llama el rango de A .

El rango de un grupo abeliano es análogo a la dimensión de un espacio vectorial . La principal diferencia con el caso del espacio vectorial es la presencia de torsión . Un elemento de un grupo abeliano A se clasifica como torsión si su orden es finito. El conjunto de todos los elementos de torsión es un subgrupo, llamado el subgrupo de torsión y se denota T ( A ). Un grupo se llama libre de torsión si no tiene elementos de torsión no triviales. El grupo de factores A / T ( A ) es el único máximo cociente sin torsión de A y su rango coincide con el rango de A.

La noción de rango con propiedades análogas se puede definir para módulos sobre cualquier dominio integral , el caso de grupos abelianos correspondientes a los módulos sobre Z . Para esto, vea el módulo genéricamente generado # rango genérico .

Propiedades [ editar ]

• El rango de un grupo abeliano A coincide con la dimensión de la Q espacio-vector A ⊗ Q . Si A no tiene torsión, el mapa canónico A → A ⊗ Q es inyectivo y el rango de A es la dimensión mínima del espacio Q-vector que contiene A como un subgrupo abeliano. En particular, cualquier grupo intermedio Z ⁿ < A < Q ⁿtiene rango n .
• Los grupos abelianos de rango 0 son exactamente los grupos abelianos periódicos .
• El grupo Q de los números racionales tiene el rango 1. Los grupos abelianos de rango 1 libres de torsión se realizan como subgrupos de Q y existe una clasificación satisfactoria de ellos hasta el isomorfismo. Por el contrario, no existe una clasificación satisfactoria de los grupos abelianos libres de torsión de rango 2. ^[2]
• El rango es aditivo en secuencias exactas cortas : si

$${\ displaystyle 0 \ to A \ to B \ to C \ to 0 \;}

es un corto secuencia exacta de los grupos abelianos entonces rk B = rk A + rk C . Esto se deduce de la planitud de Q y el hecho correspondiente para los espacios vectoriales.

• El rango es aditivo sobre sumas directas arbitrarias :

$${\ displaystyle \ operatorname {rank} \ left (\ bigoplus _ {j \ in J} A_ {j} \ right) = \ sum _ {j \ in J} \ operatorname {rank} (A_ {j}),}

Donde la suma en el lado derecho usa aritmética cardinal .

Grupos de mayor rango [ editar ]

Los grupos abelianos de rango superior a 1 son fuentes de ejemplos interesantes. Por ejemplo, para cada dcardinal existen grupos abelianos de rango d libres de torsión que no se pueden descomponer , es decir, no se pueden expresar como una suma directa de un par de sus subgrupos apropiados. Estos ejemplos demuestran que los grupos abelianos libres de torsión de rango superior a 1 no pueden construirse simplemente mediante sumas directas de grupos abelianos libres de torsión de rango 1, cuya teoría es bien entendida. Además, para cada entero n ≥ 3, hay un grupo abeliano sin torsión de rango 2 n - 2 que es simultáneamente una suma de dos grupos indecomponibles, y una suma de n grupos indecomponibles. ^{[ cita requerida]} Por lo tanto, incluso el número de sumas indecomposibles de un grupo de rango superior o igual a 4 no está bien definido.

Otro resultado sobre la no unicidad de las descomposiciones de suma directa se debe a la esquina ALS: dados los enteros n  ≥  k  ≥ 1, existe un grupo abeliano A libre de torsión de rango n tal que para cualquier partición n = r ₁ + ... + r _k en k sumas naturales, el grupo A es la suma directa de k subgrupos indecomponibles de rangos r ₁ , r ₂ , ..., r _k . ^{[ cita requerida ]}Por lo tanto la secuencia de filas de los sumandos indescomponibles en una cierta suma directa descomposición de un grupo abeliano libre de torsión de rango finito es muy lejos de ser un invariante de A .

Otros ejemplos sorprendentes incluyen los grupos de rango 2 libres de torsión A _n , m y B _{n , m , de} modo que A ⁿes isomorfo a B ⁿ si y solo si n es divisible por m .

Para los grupos abelianos de rango infinito, hay un ejemplo de un grupo K y un subgrupo G tal que

• K es indecomposible;
• K es generado por G y un solo otro elemento; y
• Todo sumando directo distinto de cero de G es descomponible.

Generalización [ editar ]

La noción de rango se puede generalizar para cualquier módulo M sobre un dominio integral R , como la dimensión sobre R ₀ , el campo de cociente , del producto tensorial del módulo con el campo:

$${\ displaystyle {\ text {rank}} (M) = \ dim _ {R_ {0}} M \ otimes _ {R} R_ {0}}

Tiene sentido, ya que R ₀ es un campo y, por lo tanto, cualquier módulo (o, para ser más específico, espacio vectorial ) sobre él es libre.

Es una generalización, ya que cualquier grupo abeliano es un módulo sobre los enteros. Se deduce fácilmente que la dimensión del producto sobre Q es la cardinalidad de un subconjunto linealmente independiente máximo, ya que para cualquier elemento de torsión x y cualquier q racional

$${\ displaystyle x \ otimes _ {\ mathbf {Z}} q = 0}

 grupo cíclico o grupo monogenous es un grupo que está generado por un único elemento. ^[1] Es decir, consiste en un conjunto de elementos con una sola operación asociativa invertible , y contiene un elemento  g tal que cualquier otro elemento del grupo se puede obtener aplicando repetidamente la operación de grupo o su inverso a  g . Cada elemento puede escribirse como una potencia de gen notación multiplicativa, o como un múltiplo de g en notación aditiva. Este elemento g se llama generador del grupo.^[1]

Cada grupo cíclico infinito es isomorfo al grupo aditivo de Z , los enteros. Cada grupo cíclico finito de orden n es isomorfo al grupo aditivo de Z / n Z , los enteros módulo n . Cada grupo cíclico es un grupo abeliano (lo que significa que su operación grupal es conmutativa ), y cada grupo abeliano finamente generado es un producto directo de grupos cíclicos.

Definición [ editar ]

Las seis sextas raíces complejas de la unidad forman un grupo cíclico bajo multiplicación. z es un elemento primitivo, pero z ²no lo es, porque las potencias impares de z no son una potencia de z ² .

Grupos cíclicos infinitos

p1, ( * ∞∞ )	p11g, (22∞)
Dos grupos friso son isomorfo a Z . Con un generador, p1 tiene traducciones y p11g tiene reflejos de planeo.

Un grupo G se llama cíclico si existe un elemento g en G tal que G = ⟨ g ⟩ = { g ⁿ | n es un número entero}. Dado que cualquier grupo generado por un elemento en un grupo es un subgrupo de ese grupo, mostrar que el único subgrupo de un grupo G que contiene g es G es suficiente para demostrar que G es cíclico.

Por ejemplo, si G = { g ⁰ , g ¹ , g ² , g ³ , g ⁴ , g ⁵ } es un grupo de orden 6, entonces g ⁶ = g ⁰ , y G es cíclico. De hecho, G es esencialmente el mismo que (es decir, isomorfo para) el conjunto {0, 1, 2, 3, 4, 5} con módulo deadición 6. Por ejemplo, 1 + 2 ≡ 3 (mod 6) corresponde a g ¹ · g ² =g ³ , y 2 + 5 ≡ 1 (mod 6) corresponde ag ² · g ⁵ = g ⁷ = g ¹ , y así sucesivamente. Se puede usar el isomorfismo χ definido por χ ( g ⁱ ) = i .

El nombre "cíclico" puede ser engañoso: ^[2] es posible generar infinitos elementos y no formar ningún ciclo literal; es decir, cada g ⁿ es distinto. (Se puede pensar que tiene un ciclo infinitamente largo). Un grupo generado de esta manera (por ejemplo, el primer grupo de frisos , p1) se llama un grupo cíclico infinito , y es isomorfo al grupo aditivo de los enteros , ( Z , +) .

La colección de matemáticos franceses que se publicaron con el nombre de Nicolas Bourbaki introdujo el término grupo monógeno para un grupo que admite un sistema de generadores que consiste en un solo elemento y restringió el término "grupo cíclico" para que signifique solo grupos monógenos finitos, evitando el término "cíclico infinito". grupo". ^{[nota 1]}

Ejemplos [ editar ]

Ejemplo de grupos cíclicos en simetría n-dimensional.

C 1	C 2	C 3
C 4	C 5	C 6

Agregado entero y modular [ editar ]

El conjunto de enteros , con la operación de suma, forma un grupo. ^[1] Es un grupo cíclico infinito , porque todos los enteros se pueden escribir como una suma o diferencia finita de copias del número 1. En este grupo, 1 y −1 son los únicos generadores. Cada grupo cíclico infinito es isomorfo a este grupo.

Para cada entero positivo n , el conjunto de enteros módulo  n , de nuevo con la operación de adición, forma un grupo cíclico finito, el grupo Z / ( n ). ^[1] Un elemento g es un generador de este grupo si g es relativamente primo a n (porque estos elementos pueden generar todos los demás elementos del grupo mediante la multiplicación de enteros). Por lo tanto, el número de generadores diferentes es φ ( n ), donde φ es la función totient de Euler , la función que cuenta el número de números módulo  nque son relativamente primos a n . Cada grupo cíclico finito es isomorfo a un grupo Z / ( n ), donde n es el orden del grupo.

Las operaciones de adición de enteros y modulares, utilizadas para definir los grupos cíclicos, son operaciones de suma de anillos conmutativos , también denominadas Z y Z / ( n ). Si p es un número primo, entonces Z / ( p ) es un campo finito , y generalmente se escribe como F _p o GF ( p ). Cada campo con p elementos es isomorfo a este.

Multiplicación modular [ editar ]

Artículo principal: Grupo multiplicador de enteros módulo n

Para cada entero positivo n , el subconjunto de los enteros módulo  n que son relativamente primos en  n , con la operación de multiplicación, forma un grupo finito que para muchos valores de n es nuevamente cíclico. Es el grupo bajo el módulo de multiplicación n , y es cíclico cuando n es 1, 2, 4, una potencia de un primo impar , o dos veces una potencia de un primo impar. ^[4] (secuencia A033948 en el OEIS ) ^[5] Sus elementos son las unidadesdel anillo Z / n Z ; hay φ( n ) de ellos, donde nuevamente φ es la función principal. Este grupo se escribe como ( Z/ n Z ) ^× . Por ejemplo, ( Z / 6 Z ) ^× tiene como elementos {1,5}; 6 es dos veces un número primo, por lo que este es un grupo cíclico. En contraste, ( Z / 8 Z ) ^× (con elementos {1,3,5,7}) es el grupo de Klein y no es cíclico. Cuando ( Z / n Z ) ^× es cíclico, cada generador (a través de la exponenciación ) de ( Z / n Z) ^× se llama un módulo raíz primitivo n .

El grupo cíclico ( Z / p Z ) ^× para un número primo p , también se escribe ( Z / p Z ) ^* porque consiste en los elementos no cero del campo finito de orden p . Más generalmente, cada subgrupo finito del grupo multiplicativo de cualquier campo es cíclico. ^[6]

Simetrías rotacionales [ editar ]

Artículo principal: Simetría rotacional.

El conjunto de simetrías rotacionales de un polígono forma un grupo cíclico finito. ^[7] Si hay n formas diferentes de mapear el polígono a sí mismo mediante una rotación (incluida la rotación nula), este grupo es isomorfo a Z _n . En tres o más dimensiones pueden existir otros grupos de simetría finitos que son cíclicos , pero que no forman el conjunto de rotaciones alrededor de un solo eje.

El grupo S ¹ de todas las rotaciones de un círculo (el grupo del círculo ) no es cíclico. A diferencia del grupo cíclico infinito, ni siquiera es contable . También existen otros grupos de rotación infinita (como el conjunto de rotaciones por ángulos racionales) que son contables pero no cíclicos.

La teoría de Galois [ editar ]

Un n º raíz de la unidad puede ser pensado como un número complejo cuya n ésima potencia es 1. Es decir, es una raíz del polinomio x ⁿ  - 1. El n º raíces de forma unidad un grupo cíclico de orden n en virtud multiplicación. ^[1] Por ejemplo, el polinomio 0 = z ³ - 1 factores como ( z - s ⁰ ) ( z - s ¹ ) ( z - s ² ) , donde s= e ^{2 πi / 3} ; el conjunto { s ⁰ , s ¹ , s ² } forma un grupo cíclico bajo multiplicación. El grupo de Galois de la extensión campo de los números racionales generados por el n º raíces de la unidad forma un grupo diferente. Es isomorfo al módulo multiplicativo  n , que tiene un orden φ ( n ) y es cíclico para algunos pero no todos  n .

Una extensión de campo se denomina extensión cíclica si su grupo Galois es un grupo cíclico. El grupo de Galois de cada extensión finita de un campo finito es finito y cíclico, con una iteración del endomorfismo de Frobeniuscomo su generador. ^[8] A la inversa, dado un campo finito F y un grupo cíclico finito G , hay una extensión campo finito de F cuya Galois grupo es G . ^[9]

Subgrupos y notación [ editar ]

Artículo principal: Teorema fundamental de los grupos cíclicos.

Todos los subgrupos y grupos cocientes de grupos cíclicos son cíclicos. Específicamente, todos los subgrupos de Z son de la forma m Z , con m un número entero ≥0. Todos estos subgrupos son distintas unas de otras, y aparte del grupo trivial (para m = 0 ) todos son isomorfo a Z . La red de subgrupos de Z es isomorfa al dual de la red de números naturales ordenados por divisibilidad . ^[10]En particular, dado que los números primos son los números sin divisores no triviales, un grupo cíclico es simple si y solo si su orden (el número de sus elementos) es primo. ^[11]

Dado que los grupos cíclicos son abelianos , a menudo se escriben de forma aditiva y se designan como Z _n con la identidad escrita 0. Sin embargo, esta notación puede ser problemática para los teóricos de los númerosporque está en conflicto con la notación habitual para los anillos de números p -adic o la localización en un momento primordial ideales . Las notaciones de cociente Z / n Z , Z / ( n ) y Z / n son alternativas de uso frecuente.

En su lugar, se puede escribir el grupo de manera multiplicativa, y denotarlo por C _n , donde n es el orden de los grupos finitos y por C para el grupo cíclico infinito. ^{[nota 2]} Por ejemplo, g ² g ⁴ = g ¹ en C ₅ , mientras que 2 + 4 = 1en Z / 5 Z .

Todos los grupos cocientes de Z son finitos, con la excepción Z / 0 Z = Z / {0}. Para cada divisor positivo d de n , el grupo cociente Z / n Z tiene precisamente un subgrupo de orden d , el generado por la clase de residuo de n / d . No hay otros subgrupos. Usando el formalismo de grupo cociente, Z / n Z es una notación estándar para el grupo cíclico aditivo con n elementos. En terminología de anillo , el subgrupo nZ también es el ideal ( n ), por lo que el cociente también se puede escribir Z / ( n ) sin abuso de notación. Estas alternativas no entran en conflicto con la notación de los enteros p -adic. La notación Z / n es común en cálculos informales.

Propiedades adicionales [ editar ]

Cada grupo cíclico es abeliano . ^[1] Es decir, su operación de grupo es conmutativa : gh = hg (para todos g y h en G ). Esto está claro para los grupos de suma de enteros y modulares desde r + s ≡ s + r (mod n ) , y se aplica a todos los grupos cíclicos, ya que todos son isomorfos a un grupo generado por una operación de suma. Para un grupo cíclico finito de orden n , y cada elemento e del grupo, e ⁿEs el elemento de identidad del grupo. Esto sigue de nuevo utilizando el isomorfismo para la adición modular, ya que kn ≡ 0 (mod n ) para cada entero k .

Si d es un divisor de n , entonces el número de elementos en Z / n que tienen el orden d es φ ( d ), y el número de elementos cuyo orden se divide d es exactamente d . Si G es un grupo finito en el que, para cada n > 0 , Gcontiene como máximo n elementos de orden que dividen n , entonces G debe ser cíclico. ^{[nota 3]} El orden de un elemento m del grupo es n /gcd ( n , m ).

El producto directo de dos grupos cíclicos Z / n y Z / m es cíclico si y solo si n y m son coprime . Así, por ejemplo, Z / 12 es el producto directo de Z / 3 y Z / 4, pero no el producto directo de Z / 6 y Z / 2. Si p es un número primo , entonces el único grupo ( hasta isomorfismo ) con p elementos es Z / p . se llama un grupo cíclico primario. El teorema fundamental de los grupos abelianos establece que cada grupo abeliano finamente generado es el producto directo de muchos grupos finitos primarios cíclicos e infinitos cíclicos. Un número n se denomina número cíclico si tiene la propiedad de que Z / n es el único grupo de orden n , que es verdadero exactamente cuando gcd ( n , φ ( n )) = 1 . ^[13] Los números cíclicos incluyen todos los números primos, pero también incluyen algunos números compuestos como 15. Sin embargo, excepto 2, todos los números cíclicos son impares. Los números cíclicos son:

1, 2, 3, 5, 7, 11, 13, 15, 17, 19, 23, 29, 31, 33, 35, 37, 41, 43, 47, 51, 53, 59, 61, 65, 67, 69, 71, 73, 77, 79, 83, 85, 87, 89, 91, 95, 97, 101, 103, 107, 109, 113, 115, 119, 123, 127, 131, 133, 137, 139, 141, 143, ... (secuencia A003277 en el OEIS )

De hecho, un número n es un número cíclico si y solo si gcd ( n , φ ( n )) = 1 , donde φ es la función totient de Euler .

La definición implica inmediatamente que los grupos cíclicos tienen grupo presentación C _∞ = ⟨ x |⟩ y C _n = ⟨ x | x ⁿ ⟩ para finito n . ^[14]

Objetos asociados [ editar ]

Representaciones [ editar ]

La teoría de la representación del grupo cíclico es un caso de base crítico para la teoría de la representación de grupos finitos más generales. En el caso complejo , una representación de un grupo cíclico se descompone en una suma directa de caracteres lineales, haciendo transparente la conexión entre la teoría de los caracteres y la teoría de la representación. En el caso característico positivo , las representaciones indescriptibles del grupo cíclico forman un modelo y una base inductiva para la teoría de la representación de grupos con subgrupos Sylow cíclicos y, más generalmente, la teoría de la representación de bloques de defecto cíclico.

Gráfico de ciclo [ editar ]

Más información: Gráfico del ciclo (álgebra).

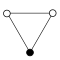
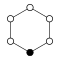
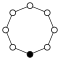
Un gráfico de ciclos ilustra los diversos ciclos de un grupo y es particularmente útil para visualizar la estructura de pequeños grupos finitos . Un gráfico de ciclo para un grupo cíclico es simplemente un gráfico circular , donde el orden del grupo es igual al número de nodos. Un solo generador define el grupo como una ruta direccional en el gráfico, y el generador inverso define una ruta hacia atrás. Las rutas triviales (identidad) se pueden dibujar como un bucle, pero generalmente se suprimen. Z ₂ se dibuja a veces con dos bordes curvos como un multigraph . ^[15]

Los grupos cíclicos Z _n , orden n , son un solo ciclo graficado simplemente como un polígono de n lados con los elementos en los vértices. Cuando n = ab con un y b ser relativamente primos (es decir, gcd ( a , b ) = 1 ), un grupo cíclico Z _n se puede descomponer en un producto directo Z _un × Z _b .

Gráficos de ciclo hasta orden 24.

Z 1	Z 2	Z 3	Z 4	Z 5	Z 6 = Z 3 × Z2	Z 7	Z 8
Z 9	Z 10 = Z 5 × Z 2	Z 11	Z 12 = Z 4 × Z 3	Z 13	Z 14 = Z 7 × Z2	Z 15 = Z 5 × Z 3	Z 16
Z 17	Z 18 = Z 9 × Z 2	Z 19	Z 20 = Z 5 × Z 4	Z 21 = Z 7 × Z 3	Z 22 = Z 11 × Z 2	Z 23	Z 24 = Z 8 × Z 3

Grafica de Cayley [ editar ]

Artículo principal: Gráfica circulatoria.

El gráfico de Paley de orden 13, un gráfico de circuito formado como el gráfico de Cayley de Z / 13 con grupo electrógeno {1,3,4}

Un gráfico de Cayley es un gráfico definido a partir de un par ( G , S ) donde G es un grupo y S es un conjunto de generadores para el grupo; tiene un vértice para cada elemento de grupo y un borde para cada producto de un elemento con un generador. En el caso de un grupo cíclico finito, con su único generador, el gráfico de Cayley es un gráfico de ciclo , y para un grupo cíclico infinito con su generador, el gráfico de Cayley es un gráfico de trayectoria doblemente infinita . Sin embargo, los gráficos de Cayley también pueden definirse a partir de otros conjuntos de generadores. Las gráficas de Cayley de grupos cíclicos con grupos generadores arbitrarios se denominan gráficas en circulación . ^[dieciséis]Estos gráficos se pueden representar geométricamente como un conjunto de puntos igualmente espaciados en un círculo o en una línea, con cada punto conectado a los vecinos con el mismo conjunto de distancias que cada otro punto. Son exactamente los gráficos transitivos de vértices cuyo grupo de simetría incluye un grupo cíclico transitivo. ^[17]

Endomorfismos [ editar ]

El anillo de endomorfismo del grupo abeliano Z / n Z es isomorfo a Z / n Z como un anillo . ^[18] Bajo este isomorfismo, el número r corresponde al endomorfismo de Z / n Z que mapea cada elemento a la suma de rcopias de él. Esta es una bijección si y solo si r es coprime con n , por lo que el grupo de automorfismo de Z / n Zes isomorfo al grupo de unidades (Z / n Z ) ^× . ^[18]

Del mismo modo, el anillo endomorphism del grupo aditivo de Z es isomorfo al anillo Z . Su grupo de automorfismo es isomorfo al grupo de unidades del anillo Z , es decir, a ({−1, +1}, ×) C ₂ .

Producto de tensor y Hom de grupos cíclicos [ editar ]

El producto tensorial. $${\ displaystyle \ mathbf {Z} / m {\ mathbf {Z}} \ otimes \ mathbf {Z} / n {\ mathbf {Z}}} y el grupo de homomorfismos. $${\ displaystyle \ hom (\ mathbf {Z} / m {\ mathbf {Z}}, \ mathbf {Z} / n {\ mathbf {Z}})} Se puede mostrar que ambos son isomorfos para $${\ displaystyle \ mathbf {Z} / \ gcd (m, n) {\ mathbf {Z}}}.

Para el producto tensorial, esto es consecuencia del hecho general. $${\ displaystyle R / I \ otimes _ {R} R / J \ cong R / (I + J)}. Para el grupo Hom, recuerde que es isomorfo para el subgrupo de$${\ displaystyle \ mathbf {Z} / n {\ mathbf {Z}}}Consta de los elementos de orden divisorio m . Ese subgrupo es cíclico de orden gcd ( m , n ) , que completa la prueba.

Clases relacionadas de grupos [ editar ]

Varias otras clases de grupos se han definido por su relación con los grupos cíclicos:

Grupos virtualmente cíclicos [ editar ]

Un grupo se llama virtualmente cíclico si contiene un subgrupo cíclico de índice finito (el número de cosets que tiene el subgrupo). En otras palabras, se puede llegar a cualquier elemento en un grupo virtualmente cíclico aplicando un miembro del subgrupo cíclico a un miembro en un determinado conjunto finito. Cada grupo cíclico es virtualmente cíclico, como lo es todo grupo finito. Un grupo infinito es virtualmente cíclico si y solo si se genera de manera finita y tiene exactamente dos extremos ; ^{[nota 4]} un ejemplo de tal grupo es el producto de Z / ( n ) y Z, en el que el factor Z tiene un índice finito n . Cada subgrupo abeliano de un grupo hiperbólico de Gromov es virtualmente cíclico. ^[20]

Grupos locales cíclicos [ editar ]

Artículo principal: Grupo localmente cíclico.

Un grupo cíclico local es un grupo en el que cada subgrupo generado de forma definitiva es cíclico. Un ejemplo es el grupo aditivo de los números racionales : cada conjunto finito de números racionales es un conjunto de múltiplos enteros de una sola fracción unitaria , el inverso de su mínimo común denominador , y genera como un subgrupo un grupo cíclico de múltiplos enteros de este fracción unitaria. Un grupo es localmente cíclico si y solo si su red de subgrupos es una red distributiva . ^[21]

Grupos en función del ciclo ordenados [ editar ]

Artículo principal: Grupo ordenado cíclicamente.

Un grupo ordenado cíclicamente es un grupo junto con un orden cíclico preservado por la estructura del grupo. A cada grupo cíclico se le puede dar una estructura como un grupo ordenado cíclicamente, consistente con el orden de los enteros (o los enteros modulo el orden del grupo). Cada subgrupo finito de un grupo ordenado cíclicamente es cíclico. ^[22]

Grupos metacíclicos y policíclicos [ editar ]

Un grupo metacíclico es un grupo que contiene un subgrupo normal cíclico cuyo cociente también es cíclico. ^[23]Estos grupos incluyen los grupos cíclicos, los grupos dicíclicos y los productos directos de dos grupos cíclicos. Los grupos policíclicos generalizan los grupos metacíclicos permitiendo más de un nivel de extensión de grupo. Un grupo es policíclico si tiene una secuencia descendente finita de subgrupos, cada uno de los cuales es normal en el subgrupo anterior con un cociente cíclico, que termina en el grupo trivial. Cada grupo abeliano o grupo nilpotente finamente generado es policíclico.