Introducción a los estados propios
Debido al principio de incertidumbre , las declaraciones sobre la posición y el momento de las partículas solo pueden asignar una probabilidad de que la posición o el momento tengan algún valor numérico. El principio de incertidumbre también dice que eliminar la incertidumbre sobre la posición maximiza la incertidumbre sobre el momento, y eliminar la incertidumbre sobre el momento maximiza la incertidumbre sobre la posición. Una distribución de probabilidad asigna probabilidades a todos los valores posibles de posición y momento. La ecuación de onda de Schrödinger da soluciones de función de onda, cuyos cuadrados son probabilidades de donde podría estar el electrón, tal como HeisenbergLa distribución de probabilidad lo hace. [1] [2] [3]
En el mundo cotidiano, es natural e intuitivo pensar que cada objeto está en su propio estado propio. Esta es otra forma de decir que cada objeto parece tener una posición definida , un momento definido , un valor medido definido y un tiempo definido de ocurrencia. Sin embargo, el principio de incertidumbre dice que es imposible medir el valor exacto para el impulso de una partícula como un electrón , dado que su posición se ha determinado en un instante dado. Del mismo modo, es imposible determinar la ubicación exacta de esa partícula una vez que se haya medido su impulso en un instante particular. [1]
Por lo tanto, se hizo necesario formular claramente la diferencia entre el estado de algo que es incierto en la forma que acabamos de describir, como un electrón en una nube de probabilidad , y el estado de algo que tiene un valor definido. Cuando un objeto definitivamente puede ser "fijado" en algún aspecto, se dice que posee un estado propio . Como se indicó anteriormente, cuando la función de onda colapsa debido a que se ha determinado la posición de un electrón, el estado del electrón se convierte en un "estado propio de la posición", lo que significa que su posición tiene un valor conocido, un valor propio del estado propio de la posición. [4]
La palabra "eigenstate" se deriva de la palabra alemana / holandesa "eigen", que significa "inherente" o "característica". Un estado propio es el estado medido de un objeto que posee características cuantificables como posición, momento, etc. El estado que se mide y describe debe ser observable (es decir, algo como posición o momento que puede medirse experimentalmente directa o indirectamente), y debe tienen un valor definido, llamado valor propio. ("Valor propio" también se refiere a una propiedad matemática de matrices cuadradas , un uso iniciado por el matemático David Hilbert en 1904. Algunas de estas matrices se llaman operadores autoadjuntos.
La mecánica cuántica es la ciencia de lo muy pequeño. Explica el comportamiento de la materia y sus interacciones con la energía en la escala de los átomos y las partículas subatómicas . En contraste, la física clásica solo explica la materia y la energía en una escala familiar a la experiencia humana, incluido el comportamiento de cuerpos astronómicos como la Luna. La física clásica todavía se utiliza en gran parte de la ciencia y la tecnología modernas. Sin embargo, hacia fines del siglo XIX, los científicos descubrieron fenómenos tanto en el mundo grande ( macro ) como en el pequeño (micro) que la física clásica no podía explicar. [1]El deseo de resolver las inconsistencias entre los fenómenos observados y la teoría clásica condujo a dos revoluciones importantes en la física que crearon un cambio en el paradigma científico original: la teoría de la relatividad y el desarrollo de la mecánica cuántica . [2] Este artículo describe cómo los físicos descubrieron las limitaciones de la física clásica y desarrollaron los conceptos principales de la teoría cuántica que la reemplazaron en las primeras décadas del siglo XX. Describe estos conceptos en aproximadamente el orden en que se descubrieron por primera vez. Para una historia más completa de la materia, vea Historia de la mecánica cuántica .
La luz se comporta en algunos aspectos como partículas y en otros aspectos como ondas. Matter-la "materia" del universo que consiste en partículas tales como electrones y átomos de -exhibits comportamiento ondulatoriotambién. Algunas fuentes de luz, como las luces de neón , emiten solo ciertas frecuencias de luz. La mecánica cuántica muestra que la luz, junto con todas las demás formas de radiación electromagnética , viene en unidades discretas, llamadas fotones , y predice sus energías, colores e intensidades espectrales . Un solo fotón es un cuanto, o la menor cantidad observable, del campo electromagnético porque nunca se ha observado un fotón parcial. En términos más generales, la mecánica cuántica muestra que muchas cantidades, como el momento angular , que aparecían continuas en la vista ampliada de la mecánica clásica, resultan cuantificadas (en la escala pequeña y ampliada de la mecánica cuántica) . Se requiere un momento angular para asumir uno de un conjunto de valores discretos permisibles, y dado que la brecha entre estos valores es tan pequeña, la discontinuidad solo es evidente a nivel atómico.
Muchos aspectos de la mecánica cuántica son contraintuitivos [3] y pueden parecer paradójicos , ya que describen un comportamiento bastante diferente del observado en escalas de mayor longitud. En palabras del físico cuántico Richard Feynman , la mecánica cuántica se ocupa de "la naturaleza tal como es: absurda". [4] Por ejemplo, el principio de incertidumbre de la mecánica cuántica significa que cuanto más estrechamente se coloque una medición (como la posición de una partícula), menos precisa será otra medición perteneciente a la misma partícula (como su momento ). .
La primera teoría cuántica: Max Planck y la radiación del cuerpo negro [ editar ]
La radiación térmica es una radiación electromagnética emitida desde la superficie de un objeto debido a la energía interna del objeto. Si un objeto se calienta lo suficiente, comienza a emitir luz en el extremo rojo del espectro , a medida que se pone al rojo vivo .
Calentarlo aún más hace que el color cambie de rojo a amarillo, blanco y azul, ya que emite luz a longitudes de onda cada vez más cortas (frecuencias más altas). Un emisor perfecto es también un absorbente perfecto: cuando hace frío, este objeto se ve perfectamente negro, porque absorbe toda la luz que cae sobre él y no emite nada. En consecuencia, un emisor térmico ideal se conoce como cuerpo negro , y la radiación que emite se llama radiación de cuerpo negro .
A finales del siglo XIX, la radiación térmica se había caracterizado bastante bien experimentalmente. [nota 1] Sin embargo, la física clásica llevó a la ley de Rayleigh-Jeans, que, como se muestra en la figura, concuerda con los resultados experimentales bien en bajas frecuencias, pero discrepa fuertemente en altas frecuencias. Los físicos buscaron una única teoría que explicara todos los resultados experimentales.
El primer modelo que pudo explicar el espectro completo de la radiación térmica fue presentado por Max Planck en 1900. [5] Propuso un modelo matemático en el que la radiación térmica estaba en equilibrio con un conjunto de osciladores armónicos . Para reproducir los resultados experimentales, tenía que asumir que cada oscilador emitía un número entero de unidades de energía en su única frecuencia característica, en lugar de poder emitir cualquier cantidad arbitraria de energía. En otras palabras, la energía emitida por un oscilador fue cuantificada . [nota 2] El cuantoLa energía para cada oscilador, según Planck, era proporcional a la frecuencia del oscilador; la constante de proporcionalidad ahora se conoce como la constante de Planck . La constante de Planck, usualmente escrita como h , tiene el valor de 6.63 × 10 −34 J s . Entonces, la energía E de un oscilador de frecuencia f está dada por
Para cambiar el color de dicho cuerpo radiante, es necesario cambiar su temperatura. La ley de Planck explica por qué: el aumento de la temperatura de un cuerpo le permite emitir más energía en general, y significa que una mayor proporción de la energía es hacia el extremo violeta del espectro.
La ley de Planck fue la primera teoría cuántica en física, y Planck ganó el Premio Nobel en 1918 "en reconocimiento a los servicios que prestó al avance de la física por su descubrimiento de los cuantos de energía". [7] En ese momento, sin embargo, la opinión de Planck era que la cuantización era puramente una construcción matemática heurística, en lugar de (como se cree ahora) un cambio fundamental en nuestra comprensión del mundo. [8]
Fotones: la cuantización de la luz [ editar ]
En 1905, Albert Einstein dio un paso más. Sugirió que la cuantización no era solo una construcción matemática, sino que la energía en un haz de luz en realidad se produce en paquetes individuales, que ahora se llaman fotones . [9] La energía de un solo fotón viene dada por su frecuencia multiplicada por la constante de Planck:
Durante siglos, los científicos habían debatido entre dos posibles teorías de la luz: ¿era una onda o en su lugar comprendía una corriente de partículas diminutas ? En el siglo XIX, se consideraba que el debate se había resuelto a favor de la teoría de la onda, ya que era capaz de explicar los efectos observados, como la refracción , la difracción , la interferencia y la polarización . [10] James Clerk Maxwell había demostrado que la electricidad, el magnetismo y la luz son manifestaciones del mismo fenómeno: el campo electromagnético . Las ecuaciones de Maxwell , que son el conjunto completo de leyes deEl electromagnetismo clásico , describe la luz como ondas: una combinación de campos eléctricos y magnéticos oscilantes. Debido a la preponderancia de la evidencia a favor de la teoría de la ola, las ideas de Einstein se encontraron inicialmente con gran escepticismo. Eventualmente, sin embargo, el modelo de fotones se volvió favorecido. Una de las pruebas más importantes a su favor fue su capacidad para explicar varias propiedades desconcertantes del efecto fotoeléctrico, que se describen en la siguiente sección. No obstante, la analogía de la onda seguía siendo indispensable para ayudar a comprender otras características de la luz: difracción , refracción e interferencia .
El efecto fotoeléctrico [ editar ]
En 1887, Heinrich Hertz observó que cuando la luz con una frecuencia suficiente golpea una superficie metálica, emite electrones. [11] En 1902, Philipp Lenard descubrió que la energía máxima posible de un electrón expulsado está relacionada con la frecuencia de la luz, no con su intensidad.: si la frecuencia es demasiado baja, no se expulsan electrones, independientemente de la intensidad. Los rayos fuertes de luz hacia el extremo rojo del espectro pueden no producir ningún potencial eléctrico, mientras que los rayos débiles hacia el extremo violeta del espectro producirán voltajes más altos y más altos. La frecuencia más baja de luz que puede hacer que se emitan electrones, llamada frecuencia de umbral, es diferente para diferentes metales. Esta observación está en desacuerdo con el electromagnetismo clásico, que predice que la energía del electrón debe ser proporcional a la intensidad de la radiación. [12] : 24 Entonces, cuando los físicos descubrieron por primera vez los dispositivos que exhibían el efecto fotoeléctrico, inicialmente esperaban que una mayor intensidad de la luz produjera un mayor voltaje del dispositivo fotoeléctrico.
Einstein explicó el efecto al postular que un haz de luz es una corriente de partículas (" fotones ") y que, si el haz es de frecuencia f , cada fotón tiene una energía igual a hf . [11] Es probable que un electrón sea golpeado por un solo fotón, que imparte a lo sumo una energía hf al electrón. [11] Por lo tanto, la intensidad del haz no tiene efecto [nota 3] y solo su frecuencia determina la energía máxima que se puede impartir al electrón. [11]
Para explicar el efecto del umbral, Einstein argumentó que se necesita una cierta cantidad de energía, llamada función de trabajo y denotada por φ , para eliminar un electrón del metal. [11] Esta cantidad de energía es diferente para cada metal. Si la energía del fotón es menor que la función de trabajo, entonces no lleva suficiente energía para eliminar el electrón del metal. La frecuencia de umbral, f 0 , es la frecuencia de un fotón cuya energía es igual a la función de trabajo:
Si f es mayor que f 0 , la energía hf es suficiente para eliminar un electrón. El electrón expulsado tiene una energía cinética , E K , que es, como máximo, igual a la energía del fotón menos la energía necesaria para desalojar el electrón del metal:
La descripción de Einstein de que la luz estaba compuesta de partículas extendió la noción de energía cuantizada de Planck, que es que un solo fotón de una frecuencia dada, f , entrega una cantidad invariante de energía, hf. En otras palabras, los fotones individuales pueden entregar más o menos energía, pero solo dependiendo de sus frecuencias. En la naturaleza, los fotones individuales rara vez se encuentran. El Sol y las fuentes de emisión disponibles en el siglo XIX emiten una gran cantidad de fotones cada segundo, por lo que la importancia de la energía transportada por cada fotón individual no era obvia. La idea de Einstein de que la energía contenida en unidades de luz individuales depende de su frecuencia hizo posible explicar los resultados experimentales que hasta ahora parecían bastante contradictorios. Sin embargo, aunque el fotón es una partícula, aún se estaba describiendo como teniendo la propiedad de frecuencia de onda. Efectivamente, el relato de la luz como una partícula es insuficiente, y su naturaleza ondulatoria aún es necesaria. [13] [nota 4]
Consecuencias de la luz siendo cuantizada [ editar ]
La relación entre la frecuencia de la radiación electromagnética y la energía de cada fotón individual es la razón por la cual la luz ultravioleta puede causar quemaduras solares , pero la luz visible o infrarroja no puede. Un fotón de luz ultravioleta proporciona una gran cantidad de energía, lo suficiente como para contribuir al daño celular, como ocurre en una quemadura solar. Un fotón de luz infrarroja entrega menos energía, solo lo suficiente para calentar la piel. Por lo tanto, una lámpara de infrarrojos puede calentar una superficie grande, tal vez lo suficientemente grande como para mantener a las personas cómodas en una habitación fría, pero no puede causar quemaduras solares a nadie. [15]
Todos los fotones de la misma frecuencia tienen una energía idéntica, y todos los fotones de diferentes frecuencias tienen proporcionalmente (orden 1, E photon = hf ) diferentes energías. [dieciséis]Sin embargo, aunque la energía impartida por los fotones es invariante en cualquier frecuencia dada, el estado de energía inicial de los electrones en un dispositivo fotoeléctrico antes de la absorción de luz no es necesariamente uniforme. Se pueden producir resultados anómalos en el caso de electrones individuales. Por ejemplo, un electrón que ya estaba excitado por encima del nivel de equilibrio del dispositivo fotoeléctrico puede ser expulsado cuando absorbe una iluminación de baja frecuencia inusualmente característica. Sin embargo, estadísticamente, el comportamiento característico de un dispositivo fotoeléctrico refleja el comportamiento de la gran mayoría de sus electrones, que se encuentran en su nivel de equilibrio. Este punto es útil para comprender la distinción entre el estudio de partículas individuales en dinámica cuántica y el estudio de partículas en masa en la física clásica. Elcita requerida ]
La cuantización de la materia: el modelo de Bohr del átomo [ editar ]
A principios del siglo XX, la evidencia requería un modelo del átomo con una nube difusa de electrones cargados negativamente que rodeaban un núcleo pequeño, denso y cargado positivamente . Estas propiedades sugieren un modelo en el que los electrones giran alrededor del núcleo como planetas que orbitan alrededor de un sol. [nota 5] Sin embargo, también se sabía que el átomo en este modelo sería inestable: según la teoría clásica, los electrones en órbita están experimentando una aceleración centrípeta y, por lo tanto, deberían emitir radiación electromagnética, la pérdida de energía también hace que giren en espiral hacia El núcleo, chocando con él en una fracción de segundo.
Un segundo rompecabezas relacionado fue el espectro de emisión de los átomos. Cuando un gas se calienta, emite luz solo en frecuencias discretas. Por ejemplo, la luz visible emitida por el hidrógeno consiste en cuatro colores diferentes, como se muestra en la siguiente imagen. La intensidad de la luz en diferentes frecuencias también es diferente. Por el contrario, la luz blanca consiste en una emisión continua en todo el rango de frecuencias visibles. A finales del siglo XIX, una regla simple conocida como la fórmula de Balmer mostraba cómo las frecuencias de las diferentes líneas se relacionaban entre sí, aunque sin explicar por quéEsto fue, o hacer cualquier predicción sobre las intensidades. La fórmula también predijo algunas líneas espectrales adicionales en luz ultravioleta e infrarroja que no se habían observado en ese momento. Estas líneas se observaron más tarde experimentalmente, aumentando la confianza en el valor de la fórmula.
espectáculo
La fórmula matemática que describe el espectro de emisión del hidrógeno.
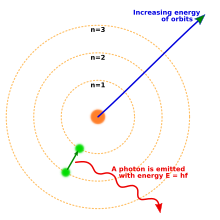
En 1913, Niels Bohr propuso un nuevo modelo del átomo que incluía órbitas electrónicas cuantificadas: los electrones todavía orbitan alrededor del núcleo como los planetas orbitan alrededor del Sol, pero solo se les permite habitar ciertas órbitas, no orbitar a ninguna distancia. [18] Cuando un átomo emitía (o absorbía) energía, el electrón no se movía en una trayectoria continua de una órbita alrededor del núcleo a otra, como podría esperarse clásicamente. En su lugar, el electrón saltaría instantáneamente de una órbita a otra, emitiendo la luz emitida en forma de fotón. [19]Las posibles energías de los fotones emitidas por cada elemento se determinaron por las diferencias de energía entre las órbitas, por lo que el espectro de emisión para cada elemento contendría un número de líneas. [20]
Partiendo de una sola suposición sobre la regla que deben obedecer las órbitas, el modelo de Bohr pudo relacionar las líneas espectrales observadas en el espectro de emisión de hidrógeno con las constantes conocidas anteriormente. En el modelo de Bohr, al electrón simplemente no se le permitía emitir energía continuamente y estrellarse contra el núcleo: una vez que estaba en la órbita más cercana permitida, estaba estable para siempre. El modelo de Bohr no explicó por qué las órbitas deberían cuantificarse de esa manera, ni era capaz de hacer predicciones precisas para los átomos con más de un electrón, o explicar por qué algunas líneas espectrales son más brillantes que otras.
Algunas suposiciones fundamentales del modelo de Bohr pronto se demostraron erróneas, pero el resultado clave de que las líneas discretas en los espectros de emisión se deben a la correcta cuantificación de algunas propiedades de los electrones en los átomos. La forma en que los electrones se comportan realmente es sorprendentemente diferente del átomo de Bohr, y de lo que vemos en el mundo de nuestra experiencia cotidiana; Este moderno modelo de mecánica cuántica del átomo se discute a continuación .










No hay comentarios:
Publicar un comentario