la botella de Klein / k l aɪ n / es un ejemplo de un no orientable superficie ; es una variedad bidimensional contra la cual no se puede definir de manera consistente un sistema para determinar un vector normal . Informalmente, es una superficie de un solo lado que, si se viaja, se puede seguir hasta el punto de origen mientras se voltea al viajero boca abajo. Otros objetos no orientables relacionados incluyen la tira de Möbius y el plano proyectivo real . Mientras que una tira de Möbius es una superficie conlímite , una botella de Klein no tiene límite (para comparación, una esfera es una superficie orientable sin límite).
La botella de Klein fue descrita por primera vez en 1882 por el matemático alemán Felix Klein . Puede haber sido originalmente llamado Kleinsche Fläche ("superficie de Klein") y luego malinterpretado como Kleinsche Flasche ("botella de Klein"), que en última instancia puede haber llevado a la adopción de este término en el idioma alemán también.
Construcción [ editar ]
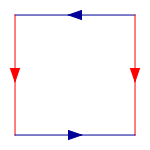
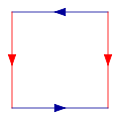
El siguiente cuadrado es un polígono fundamental de la botella de Klein. La idea es 'pegar' los bordes de colores correspondientes con las flechas que coincidan, como se muestra en los diagramas a continuación. Tenga en cuenta que este es un pegado "abstracto" en el sentido de que tratar de darse cuenta de esto en tres dimensiones da como resultado una botella Klein que se intersecta por sí misma.
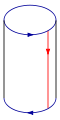
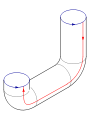
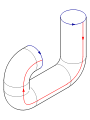
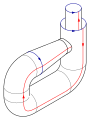
Para construir la botella Klein, pegue las flechas rojas del cuadrado (los lados izquierdo y derecho), formando un cilindro. Para pegar los extremos del cilindro juntos de modo que las flechas en los círculos coincidan, uno pasaría un extremo a través del lado del cilindro. Esto crea un círculo de auto-intersección, es una inmersión de la botella de Klein en tres dimensiones.
Esta inmersión es útil para visualizar muchas propiedades de la botella de Klein. Por ejemplo, la botella de Klein no tiene límite , donde la superficie se detiene bruscamente y no es orientable , como se refleja en la parcialidad de la inmersión.
El modelo físico común de una botella de Klein es una construcción similar. El Museo de la Ciencia de Londres tiene en exhibición una colección de botellas de vidrio Klein hechas a mano, que exhiben muchas variaciones sobre este tema topológico. Las botellas datan de 1995 y fueron hechas para el museo por Alan Bennett . [2]
La botella de Klein, propiamente dicha, no se intersecta. No obstante, hay una manera de visualizar la botella de Klein como contenida en cuatro dimensiones. Al agregar una cuarta dimensión al espacio tridimensional, se puede eliminar la auto-intersección. Empuje suavemente un pedazo del tubo que contiene la intersección a lo largo de la cuarta dimensión, fuera del espacio tridimensional original. Una analogía útil es considerar una curva de auto-intersección en el plano; las auto-intersecciones pueden eliminarse levantando una hebra del avión.
Supongamos para aclarar que adoptamos el tiempo como la cuarta dimensión. Considere cómo se podría construir la figura en xyzt -space. La ilustración adjunta ("Evolución del tiempo ...") muestra una evolución útil de la figura. En t = 0, la pared brota de un capullo en algún lugar cerca del punto de "intersección". Después de que la figura ha crecido por un tiempo, la primera sección de la pared comienza a retroceder, desapareciendo como el Gato de Cheshire, pero dejando atrás su sonrisa cada vez más amplia. Cuando el frente de crecimiento llega a donde había estado el capullo, no hay nada que intersecar y el crecimiento se complete sin perforar la estructura existente. La figura 4 como se define no puede existir en el espacio 3, pero se entiende fácilmente en el espacio 4.
Más formalmente, la botella de Klein es el espacio del cociente descrito como el cuadrado [0,1] × [0,1] con lados identificados por las relaciones (0, y ) ~ (1, y ) para 0 ≤ y ≤ 1 y ( x , 0) ~ (1 - x , 1) para 0 ≤ x ≤ 1 .
Propiedades [ editar ]
Al igual que la tira de Möbius , la botella de Klein es un colectorbidimensional que no es orientable . A diferencia de la tira de Möbius, la botella de Klein es un colector cerrado , lo que significa que es un colector compacto sin límite. Mientras que la tira de Möbius se puede incrustar en el espacio euclidiano tridimensional R 3 , la botella de Klein no puede. Sin embargo, se puede incrustar en R 4 .
La botella de Klein se puede ver como un haz de fibras sobre el círculo S 1 , con la fibra S 1 , de la siguiente manera: uno toma el cuadrado (módulo del borde que identifica la relación de equivalencia) desde arriba para que sea E , el espacio total, mientras que el espacio base B viene dado por el intervalo unitario en y , módulo 1 ~ 0 . La proyección π: E → B viene dada por π ([ x , y ]) = [ y ].
La botella de Klein se puede construir (en un sentido matemático, porque en realidad no se puede hacer sin permitir que la superficie se intersecte a sí misma) uniendo los bordes de dos tiras de Möbius, como se describe en la siguiente sección de Leo Moser : [3]
La construcción inicial de la botella de Klein al identificar los bordes opuestos de un cuadrado muestra que a la botella de Klein se le puede dar una estructura compleja de CW con una P de celda 0 , dos C 1 , C 2 y una D de 2 celdas . Su característica de Euler es, por lo tanto, 1-2 + 1 = 0. El homomorfismo límite está dado por ∂ D = 2 C 1y ∂ C 1 = ∂ C 1 = 0, lo que hace que los grupos de homología de la botella de Klein K sean H 0 ( K , Z ) =Z , H 1 ( K , Z ) = Z × ( Z / 2 Z ) y H n ( K , Z ) = 0 para n > 1.
Hay un mapa de cobertura 2-1 desde el toro hasta la botella de Klein, porque dos copias de la región fundamental de la botella de Klein, una colocada junto a la imagen especular de la otra, producen una región fundamental del toro. La cubierta universal tanto del toro como de la botella de Klein es el plano R 2 .
El grupo fundamental de la botella de Klein puede ser determinado como el grupo de transformaciones de la cubierta de la cobertura universal y tiene la presentación ⟨ un , b | ab = b -1 un ⟩ .
Seis colores son suficientes para colorear cualquier mapa en la superficie de una botella Klein; esta es la única excepción a la conjetura de Heawood , una generalización del teorema de los cuatro colores , que requeriría siete.
Una botella de Klein es homeomorfa a la suma conectada de dos planos proyectivos . También es homeomorfo a una esfera más dos casquillos cruzados .
Cuando está incrustado en el espacio euclidiano, la botella de Klein es de un solo lado. Sin embargo, hay otros 3 espacios topológicos, y en algunos de los ejemplos no orientables se puede incrustar una botella de Klein de modo que sea bilateral, aunque debido a la naturaleza del espacio no se puede orientar. [4]
Disección [ editar ]
La disección de una botella de Klein en mitades a lo largo de su plano de simetríada como resultado dos tiras de Möbius con imagen de espejo , es decir, una con una media torcedura hacia la izquierda y la otra con una media torcedura hacia la derecha (una de ellas se muestra a la derecha) . Recuerde que la intersección de la imagen no está realmente allí.
-Curvas cerradas simples [ editar ]
Una descripción de los tipos de curvas cerradas simples que pueden aparecer en la superficie de la botella de Klein está dada por el uso del primer grupo de homología de la botella de Klein calculado con coeficientes enteros. Este grupo es isomorfo a Z× Z 2.. Hasta la reversión de la orientación, las únicas clases de homología que contienen curvas cerradas simples son las siguientes: (0,0), (1,0), (1,1), (2,0), (0,1). Hasta la inversión de la orientación de una curva cerrada simple, si se encuentra dentro de una de las dos cruces que forman la botella de Klein, entonces está en la clase de homología (1,0) o (1,1); si corta la botella de Klein en dos tiras de Möbius, entonces está en clase de homología (2,0); si corta la botella de Klein en un anillo, entonces está en la clase de homología (0,1); y si limita un disco, entonces está en la clase de homología (0,0).
Parametrización [ editar ]
La figura 8 de inmersión [ editar ]
Para realizar la inmersión en "figura 8" o "bagel" de la botella de Klein, se puede comenzar con una tira de Möbius y enrollarla para llevar el borde a la línea media; Ya que solo hay un borde, se encontrará allí, pasando por la línea media. Tiene una parametrización particularmente simple como un toro "figura 8" con un medio giro:
para 0 ≤ θ <2 0="" font="" nbsp="">v <2 font="" nbsp="" y="">r > 2.
En esta inmersión, el círculo de auto-intersección (donde sen ( v ) es cero) es un círculo geométrico en el plano xy . La constante positiva r es el radio de este círculo. El parámetro θ da el ángulo en el plano xy así como la rotación de la figura 8, y v especifica la posición alrededor de la sección transversal en forma de 8. Con la parametrización anterior, la sección transversal es una curva de Lissajous 2: 1 .
4-D no intersecante [ editar ]
donde R y P son constantes que determinan la relación de aspecto, θ y v son similares a las definidas anteriormente. v determina la posición alrededor de la figura-8, así como la posición en el plano xy. θ determina también el ángulo de rotación de la figura-8 y la posición alrededor del plano zw. ε es una pequeña constante y εsin v es un pequeño bulto dependiente de v en el espacio zw para evitar la auto-intersección. La vla protuberancia hace que la figura 2-D / planar auto intersectante se extienda en una "papa frita" estilizada en 3-D o una forma de silla de montar en el borde de los espacios visto xyw y xyz. Cuando ε = 0, la auto intersección es un círculo en el plano zw <0 0="" cos="" font="" nbsp="">θ , sin θ >.
Toro 3D pellizcado / tubo 4D Möbius [ editar ]
El toro pellizcado es quizás la parametrización más simple de la botella de klein en tres y cuatro dimensiones. Es un toro que, en tres dimensiones, se aplana y pasa a través de sí mismo por un lado. Desafortunadamente, en tres dimensiones, esta parametrización tiene dos puntos de compresión, lo que hace que sea indeseable para algunas aplicaciones. En cuatro dimensiones, la amplitud z gira en la amplitud wy no hay intersecciones o puntos de pellizco.
Se puede ver esto como un tubo o cilindro que se envuelve, como en un toro, pero su sección transversal circular se voltea en cuatro dimensiones, presentando su "parte trasera" cuando se vuelve a conectar, al igual que una sección transversal de la tira de Möbius gira antes de volver a conectarse. La proyección ortogonal 3D de esto es el toro pinchado que se muestra arriba. Al igual que una tira de Möbius es un subconjunto de un toro sólido, el tubo de Möbius es un subconjunto de un esfero toroidalmente cerrado ( spheritorus sólido ).
Forma de la botella [ editar ]
La parametrización de la inmersión tridimensional de la propia botella es mucho más complicada. Aquí está una versión encontrada por Robert Israel: [ citación necesitada ]
para 0 ≤ u <π y 0 ≤ v <2 font="">
Clases de homotopía [ editar ]
Las incrustaciones regulares en 3D de la botella de Klein se dividen en tres clases de homotopía (cuatro si uno las pinta). [5] Los tres están representados por
- La botella "tradicional" de Klein.
- Botella de Klein para zurdos figura 8
- Mano derecha figura-8 botella de Klein
La incrustación de botellas Klein tradicional es aquiral . La incrustación de la figura 8 es quiral (la inserción del toro pellizcado arriba no es regular, ya que tiene puntos de aplastamiento, por lo que no es relevante en esta sección). Las tres incrustaciones anteriores no se pueden transformar suavemente entre sí en tres dimensiones. Si la botella tradicional de Klein se corta a lo largo, se deconstruye en dos tiras de Möbius opuestas de forma quiral.
Si se corta una botella de Klein de la figura 8 para zurdos, se deconstruye en dos tiras de Möbius para zurdos, y de manera similar para la botella de Klein de 8 de la mano derecha.
Si la botella tradicional de Klein está pintada en dos colores, esto induce quiralidad en ella, creando cuatro clases de homotopía.
Generalizaciones [ editar ]
La generalización de la botella de Klein a un género superior se da en el artículo sobre el polígono fundamental .
En otro orden de ideas, la construcción de 3 variedades , se sabe que una botella de Klein sólida es homeomórfica al producto cartesiano de una tira de Möbius y un intervalo cerrado. La botella sólida de Klein es la versión no orientable del toro sólido , equivalente a
Klein superficie [ editar ]
Una superficie de Klein es, como para las superficies de Riemann , una superficie con un atlas que permite componer los mapas de transición utilizando una conjugación compleja . Uno puede obtener la llamada estructura dianalítica del espacio.
superficie de Klein es una variedad dianalítica de dimensión compleja 1. Las superficies de Klein pueden tener un límite y no necesitan ser orientables . Las superficies de Klein generalizan las superficies de Riemann . Mientras que los últimos se usan para estudiar curvas algebraicas sobre los números complejos analíticamente, los primeros se usan para estudiar curvas algebraicas sobre los números reales analíticamente. Las superficies de Klein fueron introducidas por Felix Klein en 1882. [1]
Una superficie de Klein es una superficie (es decir, una variedad diferenciable de dimensión real 2) en la que la noción de ángulo entre dos vectores tangentes en un punto dado está bien definida, y también lo es el ángulo entre dos curvas de intersección en la superficie. Estos ángulos están en el rango [0, π]; Dado que la superficie no tiene noción de orientación, no es posible distinguir entre los ángulos α y −α. (Por el contrario, en Riemann, las superficies están orientadas y los ángulos en el rango de (-π, π] se pueden definir de manera significativa). La longitud de las curvas, el área de los submanifolds y la noción de geodésica no se definen en las superficies de Klein.
Dos superficies Klein X e Y se consideran equivalentes si hay mapas diferenciables conformes (es decir, preservando el ángulo pero no necesariamente preservando la orientación) f : X → Y y g : Y → X que mapean el límite al límite y satisfacen fg = id Y y gf = id X .
Ejemplos [ editar ]
Cada superficie de Riemann (variedad analítica de dimensión compleja 1, sin límite) es una superficie de Klein. Los ejemplos incluyen subconjuntos abiertos del plano complejo (no compacto), la esfera de Riemann(compacto) y tori (compacto). Tenga en cuenta que hay muchas diferentes superficies de Riemann inigualables con el mismo toro subyacente que el múltiple.
Un disco cerrado en el plano complejo es una superficie Klein (compacta, con límite). Todos los discos cerrados son equivalentes a las superficies Klein. Un anillo cerrado en el plano complejo es una superficie de Klein (compacta, con contorno). No todos los anillos son equivalentes a las superficies de Klein: hay una familia de un solo parámetro de superficies de Klein desiguales que surgen de esta manera a partir del anillo. Al eliminar una cantidad de discos abiertos de la esfera de Riemann, obtenemos otra clase de superficies Klein (compacta, con límite). El plano proyectivo real se puede convertir en una superficie Klein (compacta, sin límite), en una forma esencialmente única. La botella de kleinse puede convertir en una superficie Klein (compacta, sin límite); hay una familia de un parámetro de estructuras de superficies Klein desiguales definidas en la botella de Klein. De manera similar, hay una familia de un solo parámetro de estructuras de superficie de Klein desiguales (compacta, con límite) definida en la tira de Möbius . [2]
Cada colector 2 topológico compacto (posiblemente con límite) se puede convertir en una superficie de Klein, [3] amenudo en muchas formas diferentes de desigualdad.
Propiedades [ editar ]
El límite de una superficie compacta de Klein consta de muchos componentes conectados , cada uno de los cuales es homeomórfico para un círculo. Estos componentes se denominan óvalos de la superficie de Klein. [3]
Supongamos que Σ es una superficie de Riemann (no necesariamente conectada) y τ: Σ → Σ es una involuciónanti-holomórfica (que invierte la orientación) . Luego, el cociente Σ / τ tiene una estructura de superficie natural de Klein, y cada superficie de Klein se puede obtener de esta manera en una forma esencialmente única. [3] Los puntos fijos de τ corresponden a los puntos límite de Σ / τ. La superficie Σ se llama un "doble analítico" de Σ / τ.
Las superficies Klein forman una categoría ; un morfismo de la superficie Klein X a la superficie Klein Y es un mapa diferenciable f : X → Y que en cada parche de coordenadas es ya sea holomorphic o el conjugado complejo de un mapa holomorphic y además mapea el límite de X hasta el límite de Y .
Existe una correspondencia uno a uno entre las curvas algebraicas proyectivas suaves sobre los reales (hasta el isomorfismo ) y las superficies de Klein conectadas compactas (hasta la equivalencia). Los puntos reales de la curva corresponden a los puntos del límite de la superficie de Klein. [3] De hecho, existe una equivalencia de categorías entre la categoría de curvas algebraicas proyectivas suaves sobre R (con mapas regulares como morfismos) y la categoría de superficies compactas de Klein conectadas. Esto es similar a la correspondencia entre curvas algebraicas proyectivas suaves sobre los números complejos y las superficies compactas conectadas de Riemann. (Tenga en cuenta que las curvas algebraicas consideradas aquí son curvas abstractas: esquemas integrales , unidimensionales separados de tipo finito sobre R. Dicha curva no necesita tener ningún punto R- racional (como la curva X 2 + Y 2 + 1 = 0 sobre R ), en cuyo caso su superficie Klein tendrá un límite vacío.
También hay una correspondencia de uno a uno entre las superficies compuestas de Klein conectadas (hasta la equivalencia) y los campos de función algebraica en una variable sobre R (hasta el isomorfismo R ). Esta correspondencia es similar a la que existe entre las superficies de Riemann compactas conectadas y los campos de función algebraica sobre los números complejos. [2] Si X es una superficie de Klein, una función f : X → C u {∞} se llama meromorphic si, en cada parche de coordenadas, f o su conjugado complejo es meromorphic en el sentido ordinario, y si f toma solo valores reales (o ∞) en el límite de X. Dado un conectado Klein superficie X , el conjunto de funciones meromorfas definidos en X forman un campo M ( X ), un campo de función algebraica en una variable sobre R . M es un funtor contravariante y produce una dualidad (equivalencia contravariante) entre la categoría de superficies Klein conectadas compactas (con morfismos no constantes) y la categoría de campos de función en una variable sobre los reales.
Uno puede clasificar las superficies Klein conectadas X hasta el homeomorfismo (¡no hasta la equivalencia!) Especificando tres números ( g , k , a ): el género g del doble analítico Σ, el número k de componentes conectados del límite de X , y el número a , definido por a = 0 si X es orientable y a = 1 en caso contrario. [3]Siempre tenemos k ≤ g +1. La característica de Euler de X es igual a 1 g.


















No hay comentarios:
Publicar un comentario