Una superficie implícita es el conjunto de ceros de una función de tres variables. Implícito significa que la ecuación no se resuelve para x o y o z.
La gráfica de una función es usualmente descrita por una ecuación. y se llama una representación explícita . La tercera descripción esencial de una superficie es la paramétrica : , donde las coordenadas x -, y - yz de puntos de superficie están representadas por tres funciones dependiendo de parámetros comunes . En general, el cambio de representaciones es simple solo cuando la representación explícita es dado: (implícito), (paramétrico).
Ejemplos :
- avión
- esfera
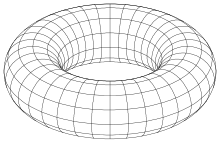
- toro
- Superficie del género 2: (ver diagrama).
- Superficie de revolucion (ver diagrama copa de vino ).
Para un plano, una esfera y un toro existen representaciones paramétricas simples. Esto no es cierto para el cuarto ejemplo.
El teorema de la función implícita describe las condiciones bajo las cuales una ecuaciónse puede resolver (al menos implícitamente) para x , y o z . Pero en general la solución puede no ser explícita. Este teorema es la clave para el cálculo de características geométricas esenciales de una superficie: planos tangentes , normales de superficie , curvaturas (ver más abajo). Pero tienen un inconveniente esencial: su visualización es difícil.
A pesar de la dificultad de visualización, las superficies implícitas proporcionan técnicas relativamente simples para generar superficies interesantes teóricamente (por ejemplo, la superficie de Steiner ) y prácticamente (ver más abajo).

Fórmulas [ editar ]
A lo largo de las siguientes consideraciones, la superficie implícita está representada por una ecuación donde funciona Cumple las condiciones necesarias de diferenciabilidad. Las derivadas parciales de son .
Plano tangente y vector normal [ editar ]
Un punto de superficie Se llama regular si y solo si el gradiente de a no es el vector cero , sentido
- .
Si el punto de superficie No es regular, se llama singular .
La ecuación del plano tangente en un punto regular es
y un vector normal es
Curvatura normal [ editar ]
Para mantener la fórmula simple los argumentos. se omiten:
es la curvatura normal de la superficie en un punto regular para la dirección tangente de la unidad . es la matriz de Hesse (matriz de las segundas derivadas).
La prueba de esta fórmula se basa (como en el caso de una curva implícita) en el teorema de la función implícita y la fórmula para la curvatura normal de una superficie paramétrica.
Aplicaciones de las superficies implícitas [ editar ]
Como en el caso de las curvas implícitas, es una tarea fácil generar superficies implícitas con las formas deseadas mediante la aplicación de operaciones algebraicas (suma, multiplicación) en primitivas simples.
Superficie equipotencial de cargas puntuales [ editar ]
El potencial eléctrico de una carga puntual. en el punto genera en el punto El potencial (omitiendo constantes físicas)
La superficie equipotencial para el valor potencial. es la superficie implícita que es una esfera con centro en el punto .
El potencial de los puntos se representan por
Para la imagen, las cuatro cargas son iguales a 1 y están ubicadas en los puntos. . La superficie mostrada es la superficie equipotencial (superficie implícita).
Superficie del producto a distancia constante [ editar ]
Un óvalo de Cassini se puede definir como el conjunto de puntos para el cual el producto de las distancias a dos puntos dados es constante (en contraste, para una elipse la suma es constante). De manera similar, las superficies implícitas se pueden definir mediante un producto de distancia constante a varios puntos fijos.
En el diagrama de metamorfosis, la superficie superior izquierda es generada por esta regla: Con
la superficie del producto a distancia constante se visualiza.
Metamorfosis de superficies implícitas [ editar ]
Otro método simple para generar nuevas superficies implícitas se llama metamorfosisde superficies implícitas:
Para dos superficies implícitas. (en el diagrama: una superficie del producto a distancia constante y un toro) se definen nuevas superficies utilizando el parámetro de diseño :
En el diagrama el parámetro de diseño es sucesivamente. .
Aproximaciones suaves de varias superficies implícitas [ editar ]
Análogamente a la aproximación suave con curvas implícitas, la ecuación
representa para los parámetros adecuados Aproximaciones suaves de tres toros que se cruzan con ecuaciones.
(En el diagrama los parámetros son )
Visualización de superficies implícitas [ editar ]
La visualización de superficies implícitas requiere un gran esfuerzo. Esencialmente hay dos ideas para visualizar una superficie implícita: una genera una red de polígonos que se visualiza (ver triangulación de la superficie ) y la segunda se basa en el trazado de rayos que determina los puntos de intersección de los rayos con la superficie.
índice elipsoide es un diagrama de un elipsoide que representa la orientación y la magnitud relativa de los índices de refracción en un cristal . [1]
La ecuación para el elipsoide se construye utilizando el vector de desplazamiento eléctrico D y las constantes dieléctricas . Definiendo la energía de campo W as
y el reducido desplazamiento como
entonces el índice elipsoide está definido por la ecuación
Los semiejes de este elipsoide son constantes dieléctricas del cristal.
Este elipsoide se puede usar para determinar la polarización de una onda entrante con un vector de ondatomando la intersección del plano Con el índice elipsoide. Los ejes de la elipse resultante son las direcciones de polarización resultantes.
Un caso especial importante del índice elipsoide ocurre cuando el elipsoide es un elipsoide de revolución, es decir, se construye girando una elipse alrededor del eje menor o mayor, cuando dos ejes son iguales y un tercero es diferente. En este caso, solo hay un eje óptico, el eje de rotación, y se dice que el material es uniaxial . Cuando todos los ejes del índice elipsoide son iguales, el material es isotrópico . En todos los demás casos, en los que el elipsoide tiene tres ejes distintos, el material se llama biaxial .
isosuperficie es un análogo tridimensional de una isolina . Es una superficie que representa puntos de un valor constante (por ejemplo, presión, temperatura, velocidad, densidad) dentro de un volumen de espacio; en otras palabras, es un conjunto de niveles de una función continua cuyo dominio es espacio 3D.
Aplicaciones [ editar ]
Las isosuperficies normalmente se muestran con gráficos de computadora y se usan como métodos de visualización de datos en dinámica de fluidos computacional (CFD), lo que permite a los ingenieros estudiar las características de un flujo de fluido (gas o líquido) alrededor de objetos, como las alas de los aviones . Una isosuperficie puede representar una onda de choque individual en vuelo supersónico , o se pueden generar varias isosuperficies que muestren una secuencia de valores de presión en el aire que fluye alrededor de un ala. Las isosuperficies tienden a ser una forma popular de visualización para los conjuntos de datos de volumen, ya que se pueden representar mediante un modelo poligonal simple, que se puede dibujar en la pantalla muy rápidamente.
En imágenes médicas , las isosuperficies se pueden usar para representar regiones de una densidad particular en una tomografía computarizada tridimensional , permitiendo la visualización de órganos internos , huesos u otras estructuras.
Muchas otras disciplinas que están interesadas en datos tridimensionales a menudo usan isosuperficies para obtener información sobre farmacología , química , geofísica y meteorología .
Algoritmos de Implementación [ editar ]
Cubos de marcha [ editar ]
El algoritmo de cubos de marcha se publicó por primera vez en los procedimientos SIGGRAPH de 1987 por Lorensen y Cline, [1] y crea una superficie al intersectar los bordes de una cuadrícula de volumen de datos con el contorno del volumen. Donde la superficie cruza el borde, el algoritmo crea un vértice. Al usar una tabla de diferentes triángulos dependiendo de los diferentes patrones de intersecciones de borde, el algoritmo puede crear una superficie. Este algoritmo tiene soluciones para la implementación tanto en la CPU como en la GPU.
Asintótica Decididor [ editar ]
El algoritmo de decisión asintótica se desarrolló como una extensión de los cubos en marcha para resolver la posibilidad de ambigüedad en él.
Marchando Tetraedros [ editar ]
El algoritmo de tetraedros de marcha se desarrolló como una extensión de los cubos de marcha para resolver una ambigüedad en ese algoritmo y crear una superficie de salida de mayor calidad.
Redes de superficie [ editar ]
El algoritmo de Surface Nets coloca un vértice de intersección en medio de un vóxel de volumen en lugar de en los bordes, lo que lleva a una superficie de salida más suave.
Contorno dual [ editar ]
El algoritmo de contorno dual se publicó por primera vez en los procedimientos SIGGRAPH de 2002 de Ju y Losasso, [2] desarrollado como una extensión de ambas redes de superficie y cubos en marcha . Retiene el vértice en el centro del vóxel, pero agrega una generación de superficie que aprovecha octetos para agregar soporte para la geometría que adapta el número de triángulos en la salida a la complejidad de la superficie.
Ejemplos [ editar ]
Ejemplos de isosuperficies son " Metaballs " u "objetos blobby" utilizados en la visualización 3D. Una forma más general de construir una superficie iso es utilizar la representación de la función .








































![\ mu \ en [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/030ca0eebf53f89d13f475805d065c80355c9390)





![{\ displaystyle {\ begin {alineado} F_ {1} = (x ^ {2} + y ^ {2} + z ^ {2} + R ^ {2} -a ^ {2}) ^ {2} - 4R ^ {2} (x ^ {2} + y ^ {2}) = 0, \\ [3pt] F_ {2} = (x ^ {2} + y ^ {2} + z ^ {2} + R ^ {2} -a ^ {2}) ^ {2} -4R ^ {2} (x ^ {2} + z ^ {2}) = 0, \\ [3pt] F_ {3} = (x ^ {2} + y ^ {2} + z ^ {2} + R ^ {2} -a ^ {2}) ^ {2} -4R ^ {2} (y ^ {2} + z ^ {2 }) = 0. \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/157d62dcc5f451b1e5f561bd248a425e1f97b28f)








No hay comentarios:
Publicar un comentario