FORMAS GEOMÉTRICAS - SUPERFICIES

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Una superficie gaussiana cilíndrica se usa comúnmente para calcular la carga eléctrica de un cable "ideal" infinitamente largo y recto.

Una superficie gaussiana (a veces abreviada como GS) es una superficie cerrada en un espacio tridimensional a través del cual se calcula el flujo de un campo vectorial ; Por lo general, el campo gravitatorio , el campo eléctrico o el campo magnético . ^[1] Se trata de una arbitraria superficie cerrada S = ∂ V (el límite de una región 3-dimensional V ) se utiliza en conjunción con la ley de Gauss para el campo correspondiente ( la ley de Gauss , la ley de Gauss para el magnetismo , o la ley de Gauss para la gravedad) realizando una integral de superficie , para calcular la cantidad total de la cantidad de la fuente incluida; por ejemplo, cantidad de masa gravitatoria como fuente del campo gravitatorio o cantidad de carga eléctrica como fuente del campo electrostático, o viceversa: calcule los campos para la distribución de la fuente.

Para concretar, el campo eléctrico se considera en este artículo, ya que este es el tipo de campo más frecuente para el que se utiliza el concepto de superficie.

Las superficies gaussianas generalmente se eligen con cuidado para explotar las simetrías de una situación para simplificar el cálculo de la integral de superficie . Si se elige la superficie gaussiana de modo que para cada punto de la superficie, la componente del campo eléctrico a lo largo del vector normal sea ​​constante, entonces el cálculo no requerirá una integración difícil ya que las constantes que surgen pueden eliminarse de la integral.

Superficies gaussianas comunes [ editar ]

Ver también: densidad de carga.

Ejemplos de superficies gaussianas válidas (izquierda) e inválidas (derecha). Izquierda:algunas superficies gaussianas válidas incluyen la superficie de una esfera, la superficie de un toro y la superficie de un cubo. Son superficies cerradas que encierran completamente un volumen 3D. Derecha: algunas superficies que NO PUEDEN usarse como superficies gaussianas, como la superficie del disco , la superficie cuadrada o la superficie del hemisferio. No encierran completamente un volumen 3D, y tienen límites (rojo). Tenga en cuenta que los planos infinitos pueden aproximarse a las superficies gaussianas.

La mayoría de los cálculos que utilizan superficies gaussianas comienzan con la implementación de la ley de Gauss (para electricidad): ^[2]

$${\ displaystyle \ Phi _ {E} = \, \!} $${\ displaystyle \ scriptstyle S \!} $${\ displaystyle \ mathbf {E} \; \ cdot \ mathrm {d} \ mathbf {A} = {\ frac {Q_ {enc}} {\ varepsilon _ {0}}}. \, \!}

De este modo, Q _enc es la carga eléctrica encerrada por la superficie gaussiana.

Esta es la ley de Gauss, que combina el teorema de la divergencia y la ley de Coulomb .

Superficie esférica [ editar ]

Se utiliza una superficie gaussiana esférica cuando se encuentra el campo eléctrico o el flujo producido por cualquiera de los siguientes: ^[3]

• un punto de carga
• Una envoltura esférica de carga uniformemente distribuida.
• Cualquier otra distribución de carga con simetría esférica.

La superficie gaussiana esférica se elige de modo que sea concéntrica con la distribución de carga.

Como un ejemplo, considere una concha esférica cargada S de espesor despreciable, con una distribución uniforme de carga Q y el radio R . Podemos usar la ley de Gauss para encontrar la magnitud del campo eléctrico E resultante a una distancia r del centro de la cáscara cargada. Es inmediatamente evidente que para una superficie gaussiana esférica de radio r < R, la carga encerrada es cero: por lo tanto, el flujo neto es cero y la magnitud del campo eléctrico en la superficie gaussiana también es 0 (al dejar Q _A = 0 en Gauss ley, donde Q _A es la carga encerrada por la superficie gaussiana).

Con el mismo ejemplo, al usar una superficie gaussiana más grande fuera de la cáscara donde r > R , la ley de Gauss producirá un campo eléctrico distinto de cero. Esto se determina de la siguiente manera.

El flujo que sale de la superficie esférica S es:

$${\ displaystyle \ Phi _ {E} = \, \!} $${\ displaystyle \ scriptstyle \ parcial S \, \!} $${\ displaystyle \ mathbf {E} \ cdot d \ mathbf {A} = \ int \! \! \! \ int _ {c} EdA \ cos 0 ^ {\ circ} = E \ int \! \! \! \! \ int _ {S} dA \, \!}

El área superficial de la esfera de radio r es

$${\ displaystyle \ int \! \! \! \! \ int _ {S} dA = 4 \ pi r ^ {2}}

lo que implica

$${\ displaystyle \ Phi _ {E} = E4 \ pi r ^ {2}}

Por la ley de Gauss el flujo también es

$${\ displaystyle \ Phi _ {E} = {\ frac {Q_ {A}} {\ varepsilon _ {0}}}}

finalmente, al igualar la expresión de Φ _{E se} obtiene la magnitud del campo E en la posición r :

$${\ displaystyle E4 \ pi r ^ {2} = {\ frac {Q_ {A}} {\ varepsilon _ {0}}} \ quad \ Rightarrow \ quad E = {\ frac {Q_ {A}} {4 \ pi \ varepsilon _ {0} r ^ {2}}}.}

Este resultado no trivial muestra que cualquier distribución esférica de carga actúa como una carga puntualcuando se observa desde el exterior de la distribución de carga; Esto es, de hecho, una verificación de la ley de Coulomb . Y, como se mencionó, los cargos exteriores no cuentan.

Superficie cilíndrica [ editar ]

Se utiliza una superficie gaussiana cilíndrica cuando se encuentra el campo eléctrico o el flujo producido por cualquiera de los siguientes: ^[3]

• Una línea infinitamente larga de carga uniforme.
• Un plano infinito de carga uniforme.
• Un cilindro infinitamente largo de carga uniforme.

Como ejemplo, "campo cerca de carga de línea infinita" se muestra a continuación;

Considere un punto P a una distancia r de una carga de línea infinita que tiene densidad de carga (carga por unidad de longitud) λ. Imagine una superficie cerrada en forma de cilindro cuyo eje de rotación es la línea de carga. Si h es la longitud del cilindro, entonces la carga incluida en el cilindro es

$${\ displaystyle q = \ lambda h},

donde q es la carga encerrada en la superficie gaussiana. Hay tres superficies a , b y c, como se muestra en la figura. El diferencial de área vector es d A , en cada superficie una , b y c .

Superficie cerrada en forma de un cilindro que tiene una línea de carga en el centro y que muestra áreas diferenciales d A de las tres superficies.

El flujo que pasa consiste en las tres contribuciones:

$${\ displaystyle \ Phi _ {E} = \, \!} $${\ displaystyle \ scriptstyle A \, \!} $${\ displaystyle \ mathbf {E} \ cdot d \ mathbf {A} = \ int \! \! \! \ int _ {a} \ mathbf {E} \ cdot d \ mathbf {A} + \ int \ ! \! \! \! \ int _ {b} \ mathbf {E} \ cdot d \ mathbf {A} + \ int \! \! \! \! \ int _ {c} \ mathbf {E} \ cdot d \ mathbf {A}}

Para las superficies a y b, E y d A serán perpendiculares . Para la superficie c, E y d Aserán paralelos , como se muestra en la figura.

{\ displaystyle {\ begin {alineado} \ Phi _ {E} & = \ int \! \! \! \! \ int _ {a} EdA \ cos 90 ^ {\ circ} + \ int \! \! \ ! \! \ int _ {b} EdA \ cos 90 ^ {\ circ} + \ int \! \! \! \ int \ {c} EdA \ cos 0 ^ {\ circ} \\ & = E \ int \! \! \! \! \ int _ {c} dA \\\ end {alineado}}}

El área superficial del cilindro es

$${\ displaystyle \ int \! \! \! \! \ int _ {c} dA = 2 \ pi rh}

lo que implica

$${\ displaystyle \ Phi _ {E} = E2 \ pi rh}

Por la ley de gauss

$${\ displaystyle \ Phi _ {E} = {\ frac {q} {\ varepsilon _ {0}}}}

equiparando para yield _E rendimientos

$${\ displaystyle E2 \ pi rh = {\ frac {\ lambda h} {\ varepsilon _ {0}}} \ quad \ Rightarrow \ quad E = {\ frac {\ lambda} {2 \ pi \ varepsilon _ {0} r}}}

Pastillero gaussiano [ editar ]

Esta superficie se usa con mayor frecuencia para determinar el campo eléctrico debido a una hoja de carga infinita con densidad de carga uniforme, o una placa de carga con un espesor finito. El pastillero tiene una forma cilíndrica, y se puede considerar que consta de tres componentes: el disco en un extremo del cilindro con área πR², el disco en el otro extremo con área igual y el lado del cilindro. La suma del flujo eléctrico a través de cada componente de la superficie es proporcional a la carga encerrada del pastillero, según lo dictado por la Ley de Gauss. Debido a que el campo cercano a la hoja se puede aproximar como constante, el pastillero está orientado de manera que las líneas del campo penetren en los discos en los extremos del campo en un ángulo perpendicular y el lado del cilindro es paralelo a las líneas del campo .

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Helicoide generalizado: meridiano es una parábola.

En geometría, un helicoide generalizado es una superficie en el espacio euclidiano que se genera al rotar y al mismo tiempo desplazar una curva, la curva de perfil , a lo largo de una línea, su eje . Cualquier punto de la curva dada es el punto de inicio de una hélice circular . Si la curva de perfil está contenida en un plano a través del eje, se denomina meridiano del helicoide generalizado. Ejemplos simples de helicoides generalizados son los helicoides . El meridiano de un helicoide es una línea que intersecta el eje ortogonalmente.

Tipos esenciales de helicoides generalizados son

• Helicoides generalizados regidos . Sus curvas de perfil son líneas y las superficies son superficies regladas .
• Helicoides circulares generalizados . Sus curvas de perfil son círculos.

En matemáticas los helicoides juegan un papel esencial como superficies mínimas . En el área técnica, los helicoides generalizados se utilizan para escaleras, correderas, tornillos y tuberías.

Representación analítica [ editar ]

Movimiento del tornillo de un punto 
verde: paso, 
azul: eje del tornillo

Movimiento de tornillo de un punto [ editar ]

Si se mueve un punto en una curva tipo tornillo, el punto se gira y se desplaza a lo largo de una línea (eje) de modo que el desplazamiento sea proporcional al ángulo de rotación. El resultado es una hélice circular .

Si el eje es el eje z , el movimiento de un punto$${\ displaystyle P_ {0} = (x_ {0}, y_ {0}, z_ {0})} puede ser descrito paramétricamente por

$${\ displaystyle \ mathbf {p} (\ varphi) = {\ begin {pmatrix} x_ {0} \ cos \ varphi -y_ {0} \ sin \ varphi \\ x_ {0} \ sin \ varphi + y_ {0 } \ cos \ varphi \\ z_ {0} + c \; \ varphi \ end {pmatrix}} \, \ \ varphi \ in \ mathbb {R} \.}

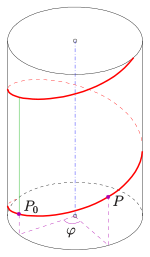
$${\ displaystyle c \ neq 0}se llama inclinación , el ángulo$${\ displaystyle \ varphi}, medido en radianes, se llama ángulo de tornillo y$${\ displaystyle h = c \; 2 \ pi}El tono (verde). La traza del punto es una hélice circular (roja). Está contenida en la superficie de un cilindro circular derecho . Su radio es la distancia del punto. $${\ displaystyle P_ {0}}al eje z

En caso de {\ displaystyle c> 0}, la hélice se llama zurda o zurda . (En caso de$${\ displaystyle c = 0}el movimiento es una rotación alrededor del eje z ).

Movimiento de tornillo de una curva [ editar ]

El movimiento del tornillo de la curva.

$${\ displaystyle \ mathbf {x} (t) = (x (t), y (t), z (t)) ^ {T}, \ t_ {1} \ leq t \ leq t_ {2} \,}

Se obtiene un helicoide generalizado con la representación paramétrica.

• $${\ displaystyle \ mathbf {S} (t, \ varphi) = {\ begin {pmatrix} x (t) \ cos \ varphi -y (t) \ sin \ varphi \\ x (t) \ sin \ varphi + y (t) \ cos \ varphi \\ z (t) + c \; \ varphi \ end {pmatrix}} \, \ quad t_ {1} \ leq t \ leq t_ {2}, \ \ varphi \ in \ mathbb {R} \.}

Las curvas $${\ displaystyle \ mathbf {S} (t = {\ text {constant}}, \ varphi)}Son hélices circulares. 
Las curvas$${\ displaystyle \ mathbf {S} (t, \ varphi = {\ text {constant}})} Son copias de la curva de perfil dada.

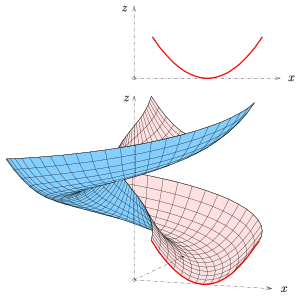
Ejemplo: Para la primera imagen de arriba, el meridiano es una parábola .

Helicoides generalizadas gobernados [ editar ]

Helicoide generalizado de derecha: cerrado (izquierda) y abierto (derecha)

Tipos oblicuos: cerrado (izquierda) y abierto (derecha)

Tipo de tangente desarrollable: definición (izquierda) y ejemplo

Tipos [ editar ]

Si la curva de perfil es una línea, se obtiene un helicoide generalizado descartado . Hay cuatro tipos:

(1) La línea intersecta el eje ortogonalmente. Uno recibe un helicoide ( helicoide generalizado cerrado a la derecha cerrado ).

(2) La línea corta el eje, pero noortogonalmente. Uno obtiene un tipo cerrado oblicuo .

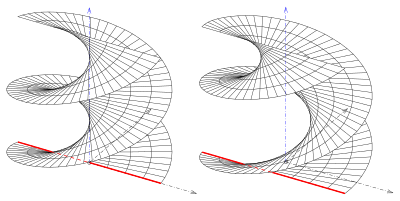
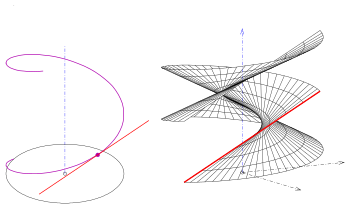
Si la línea y el eje dados son líneas oblicuas, se obtiene un tipo abierto y el eje no es parte de la superficie (s. Imagen).

(3) Si la línea y el eje dados son líneas oblicuas y la línea está contenida en un plano ortogonal al eje, se obtiene un tipo de apertura derecha o un helicoidepoco abierto .

(4) Si la línea y el eje están sesgados y la línea no está contenida en ... (s. 3), se obtiene un tipo abierto oblicuo .

Los tipos oblicuos se intersecan entre sí (s. Imagen), los tipos correctos (helicoides) no.

Se obtiene un caso interesante, si la línea está sesgada al eje y el producto de su distancia. $${\ displaystyle d} al eje y su pendiente es exactamente $${\ displaystyle c}. En este caso, la superficie es una superficie tangible desarrollable y es generada por la directriz $${\ displaystyle (d \ cos \ varphi, d \ sin \ varphi, c \ varphi)}.

Observación:

1. Los helicoides (abiertos y cerrados) son superficies catalanas . El tipo cerrado (helicoide común) es incluso un conoide
2. Los helicoides gobernados generalizados no son superficies algebraicas.

Sobre helicoides generalizados de regla cerrada [ editar ]

En la auto sección de helicoides generalizados de regla cerrada.

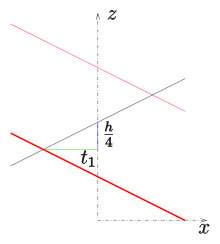
Un helicoide generalizado de regla cerrada tiene una línea de perfil que corta el eje. Si la línea de perfil está descrita por $${\ displaystyle (t, 0, z_ {0} + m \; t) ^ {T}} uno obtiene la siguiente representación paramétrica

• $${\ displaystyle \ mathbf {S} (t, \ varphi) = {\ begin {pmatrix} t \ cos \ varphi \\ t \ sin \ varphi \\ z_ {0} + mt + c \ varphi \ end {pmatrix} } \.}

Si $${\ displaystyle m = 0}(helicoide común) la superficie no se interseca. 
Si$${\ displaystyle m \ neq 0} (tipo oblicuo) la superficie se interseca con las curvas (en la superficie)

$${\ displaystyle \ mathbf {S} (t_ {i}, \ varphi)} con $${\ displaystyle t_ {i} = {\ frac {h} {4m}} (2i + 1), \ i = 1,2, \ ldots}

consisten en puntos dobles . Existen infinitas curvas dobles. El pequeño $${\ displaystyle | m |} cuanto mayores son las distancias entre las curvas dobles.

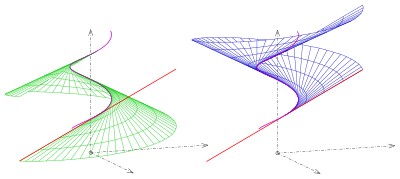
En el tipo de tangente desarrollable [ editar ]

tangente desarrollable: partes regulares (verde y azul) y la directriz (púrpura)

Para la directriz (una hélice)

$${\ displaystyle \ mathbf {x} (\ varphi) = (r \ cos \ varphi, r \ sin \ varphi, c \ varphi) ^ {T}}

uno obtiene la siguiente representación paramétrica de la superficie tangible de desarrollo:

• $${\ displaystyle \ mathbf {S} (t, \ varphi) = \ mathbf {x} (\ varphi) + t \ mathbf {\ dot {x}} (\ varphi) = {\ begin {pmatrix} r \ cos \ varphi -tr \ sin \ varphi \\ r \ sin \ varphi + tr \ cos \ varphi \\ c (t + \ varphi) \ end {pmatrix}} \.}

El vector normal de superficie es

$${\ displaystyle \ mathbf {n} = \ mathbf {S} _ {t} \ times \ mathbf {S} _ {\ varphi} = \ mathbf {\ dot {x}} \ times (\ mathbf {\ dot {x }} + t \ mathbf {\ ddot {x}}) = t (\ mathbf {\ dot {x}} \ times \ mathbf {\ ddot {x}}) = t {\ begin {pmatrix} cr \ sin \ varphi \\ - cr \ cos \ varphi \\ r ^ {2} \ end {pmatrix}} \.}

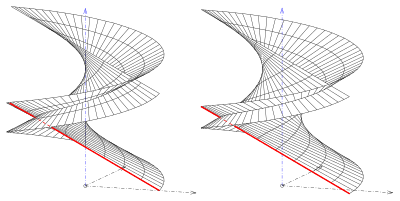
por $${\ displaystyle t = 0}el vector normal es el vector nulo De ahí que la directriz consista en puntos singulares. La directriz separa dos partes regulares de la superficie (s. Imagen).

Helicoides circulares generalizados [ editar ]

meridiano es un círculo

La curva de perfil es un círculo horizontal.

Hay 3 tipos interesantes de helicoides circulares generalizados:

(1) Si el círculo es un meridiano y no se interseca con los ejes (s. Imagen).

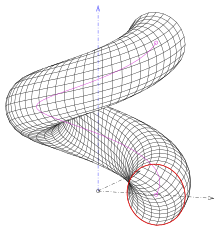
(2) El plano que contiene el círculo es ortogonal a la hélice de los centros circulares. Uno obtiene una superficie de tubería

(3) El plano del círculo es ortogonal al eje y comprende el punto del eje en él (s. Imagen). Este tipo fue utilizado para columnas barrocas.

• 

  Escalera, Universidad de Mannheim, Alemania
• 

  tubo deslizante Salinarium
• 

  altar (1688), San Pankracio, Neuenfelde, Alemania