FORMAS GEOMÉTRICAS - SUPERFICIES

pseudosfera es una superficie con una curvatura gaussiana negativa constante . El teorema de Hilbert dice que ninguna pseudosfera puede sumergirse en el espacio tridimensional.

Descripción más detallada de la pseudosfera [ editar ]

Una pseudosfera de radio R es una superficie en$${\ displaystyle \ mathbb {R} ^ {3}}teniendo curvatura - 1/R ² en cada punto. Su nombre proviene de la analogía con la esfera de radio R , que es una superficie de curvatura 1/R ² . El término fue introducido por Eugenio Beltrami en su artículo de 1868 sobre modelos de geometría hiperbólica . ^[1]

Tractricoid [ editar ]

Tractricoides

La misma superficie también se puede describir como el resultado de girar una tractrix sobre su asíntota . Por esta razón, la pseudosfera también se llama tractricoid . Como ejemplo, la (media) pseudosfera (con radio 1) es la superficie de revolución de la tractrix parametrizada por ^[2]

{\ displaystyle t \ mapsto \ left (t- \ tanh {t}, \ operatorname {sech} \, {t} \ right), \ quad \ quad 0 \ leq t <\ infty.}

Es un espacio singular (el ecuador es una singularidad), pero alejado de las singularidades, tiene una curvatura gaussiananegativa constante y, por lo tanto, es localmente isométrico a un plano hiperbólico .

El nombre de "pseudosfera" surge porque es una superficie bidimensional de curvatura negativa constante, como una esfera con una curvatura de Gauss positiva. Así como la esfera tiene en cada punto una geometría curvada positivamente de una cúpula, toda la pseudosfera tiene en cada punto la geometría curvada negativamente de una silla .

Ya en 1693, Christiaan Huygens descubrió que el volumen y el área de superficie de la pseudosfera son finitos, ^{[3] a} pesar de la infinita extensión de la forma a lo largo del eje de rotación. Para un borde dado radio R , el áreaes 4π R ² tal como es para la esfera, mientras que el volumen es 2/3 π R ³ y por lo tanto la mitad del de una esfera de ese radio. ^[4] [5]

Espacio de cobertura universal [ editar ]

La media pseudoesfera de curvatura −1 está cubierta por la porción del plano medio hiperbólico superior con y ≥ 1 . ^[6] El mapa de cobertura es periódico en la dirección x del período 2 π , y lleva los horociclos y = c a los meridianos de la pseudosfera y las geodésicas verticales x = c a las tractrices que generan la pseudosfera. Este mapeo es una isometría local, y por lo tanto exhibe la porción y ≥ 1 del semiplano superior como el espacio de cobertura universal de la pseudosfera. El mapeo preciso es

$${\ displaystyle (x, y) \ mapsto {\ big (} v (\ operatorname {arcosh} y) \ cos x, v (\ operatorname {arcosh} y) \ sin x, u (\ operatorname {arcosh} y) {\grande )}}

dónde

$${\ displaystyle t \ mapsto {\ big (} u (t) = t- \ operatorname {tanh} t, v (t) = \ operatorname {sech} t {\ big)}}

Es la parametrización de la tractrix anterior.

Hyperboloid [ editar ]

En algunas fuentes que utilizan el modelo hiperboloide del plano hiperbólico, el hiperboloide se conoce como una pseudoesfera . ^[7] Este uso de la palabra se debe a que el hiperboloide se puede considerar como una esfera de radio imaginario, incrustada en un espacio Minkowski .

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

El polígono fundamental del plano proyectivo.

La tira de Möbiuscon un solo borde, se puede cerrar en un plano proyectivo pegando los bordes opuestos juntos.

En comparación, labotella Klein es una tira de Möbius cerrada en un cilindro.

En matemáticas , el plano proyectivo real es un ejemplo de un colector bidimensional no orientable compacto ; en otras palabras, una superficie unilateral . No se puede incrustar en el espacio tridimensional estándar sin intersecarse. Tiene aplicaciones básicas para la geometría , ya que la construcción común del plano proyectivo real es como el espacio de líneas en R ^{3 que} pasa por el origen.

El plano a menudo también se describe topológicamente, en términos de una construcción basada en la tira de Möbius : si se pudiera pegar el borde (único) de la tira de Möbius en la dirección correcta, se obtendría el plano proyectivo. (Esto no se puede hacer en el espacio tridimensional). De manera equivalente, pegar un disco a lo largo del límite de la tira de Möbius da el plano proyectivo. Topológicamente, tiene la característica 1 de Euler , de ahí un demigenus (género no orientable, género Euler) de 1.

Como la tira de Möbius, a su vez, puede construirse a partir de un cuadrado pegando dos de sus lados, el plano proyectivo real puede representarse como una unidad cuadrada (es decir, [0,1] × [0,1]) Con sus lados identificados por las siguientes relaciones de equivalencia :

(0, y ) ~ (1, 1 - y ) para 0 ≤  y  ≤ 1

y

( x , 0) ~ (1 - x , 1) para 0 ≤  x  ≤ 1,

como en el diagrama de la izquierda que se muestra aquí.

Ejemplos [ editar ]

La geometría proyectiva no tiene que ver necesariamente con la curvatura y el plano proyectivo real puede torcerse y ubicarse en el plano euclidiano o espacio 3 en muchas formas diferentes. ^[1] Algunos de los ejemplos más importantes se describen a continuación.

El plano proyectivo no se puede incrustar (es decir, sin intersección) en el espacio euclidiano tridimensional . La prueba de que el plano proyectivo no se incrusta en el espacio euclidiano tridimensional es la siguiente: suponiendo que se incruste, se uniría una región compacta en el espacio euclidiano tridimensional mediante el teorema de la curva de Jordan generalizada . El campo vectorial normal de la unidad que apunta hacia el exterior daría entonces una orientación del colector de límites, pero el colector de límites sería el plano proyectivo , que no es orientable. Esto es una contradicción, por lo que nuestra suposición de que sí se incrusta debe haber sido falsa.

La esfera proyectiva [ editar ]

Considera una esfera , y deja que los grandes círculos de la esfera sean "líneas", y deja que los pares de puntos antípodas sean "puntos". Es fácil comprobar que este sistema obedece a los axiomas requeridos de un plano proyectivo :

• cualquier par de grandes círculos distintos se encuentran en un par de puntos antípodas; y
• cualquiera de los dos pares distintos de puntos antípodas se encuentran en un solo gran círculo.

Si identificamos cada punto en la esfera con su punto antípodas, entonces obtenemos una representación del plano proyectivo real en el que los "puntos" del plano proyectivo realmente son puntos. Esto significa que el plano proyectivo es el espacio de cociente de la esfera obtenido al dividir la esfera en clases de equivalencia bajo la relación de equivalencia ~, donde x ~ y si y = −x. Este espacio de cociente de la esfera es homeomórfico con la colección de todas las líneas que pasan por el origen en R ³ .

El mapa de cociente de la esfera al plano proyectivo real es, de hecho, un mapa de cobertura de dos hojas (es decir, de dos a uno) . De ello se deduce que el grupo fundamental del plano proyectivo real es el grupo cíclico de orden 2, es decir, enteros módulo 2. Uno puede tomar el bucle AB de la figura de arriba para ser el generador.

El hemisferio proyectiva [ editar ]

Debido a que la esfera cubre el plano proyectivo real dos veces, el plano puede representarse como un hemisferio cerrado alrededor de cuyo borde se identifican de manera similar los puntos opuestos. ^[2]

La superficie del niño - una inmersión [ editar ]

El plano proyectivo puede sumergirse (los vecindarios locales del espacio fuente no tienen auto-intersecciones) en 3 espacios. La superficie del niño es un ejemplo de inmersión.

Los ejemplos poliédricos deben tener al menos nueve caras. ^[3]

Romana la superficie [ editar ]

Una animación de la superficie romana.

La superficie romana de Steiner es un mapa más degenerado del plano proyectivo en 3 espacios, que contiene una tapa cruzada .

El tetrahemihexaedro es una representación poliédrica del plano proyectivo real.

Una representación poliédrica es el tetrahemihexaedro , ^[4] que tiene la misma forma general que la Superficie romana de Steiner, que se muestra aquí.

Hemi poliedros [ editar ]

Mirando en la dirección opuesta, ciertos polytopes regulares abstractos ( hemicubo , hemododecaedro y hemicosaedro ) se pueden construir como figuras regulares en el plano proyectivo; Ver también poliedros proyectivos .

Proyecciones planas [ editar ]

Se han descrito varias proyecciones planas (planas) o mapeos del plano proyectivo. En 1874 Klein describió el mapeo.$${\ displaystyle k (x, y) = (1 + x ^ {2} + y ^ {2}) ^ {1/2}. (x, y)} ^[1]

La proyección central del hemisferio proyectivo en un plano produce el plano proyectivo infinito habitual, que se describe a continuación.

Disco-Cruz cubiertas [ editar ]

Una superficie cerrada se obtiene pegando un disco a una tapa cruzada . Esta superficie se puede representar paramétricamente mediante las siguientes ecuaciones:

$${\ displaystyle X (u, v) = r \, (1+ \ cos v) \, \ cos u,}

$${\ displaystyle Y (u, v) = r \, (1+ \ cos v) \, \ sin u,}

$${\ displaystyle Z (u, v) = - {\ hbox {tanh}} \ left (u- \ pi \ right) \, r \, \ sin v,}

donde tanto u como v van de 0 a 2 π . Estas ecuaciones son similares a las de un toro . La figura 1 muestra un disco cerrado de tapa cruzada.

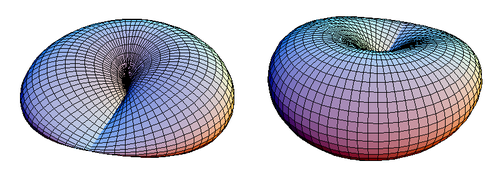Figura 1. Dos vistas de un disco de tapa cruzada.

Un disco con tapa cruzada tiene un plano de simetría que pasa a través de su segmento de línea de puntos dobles. En la Figura 1, el disco con topes cruzados se ve desde arriba de su plano de simetría z = 0, pero se vería igual si se ve desde abajo.

Un disco con tapa cruzada puede abrirse en cortes a lo largo de su plano de simetría, mientras se asegura de no cortar ninguno de sus puntos dobles. El resultado se muestra en la Figura 2.

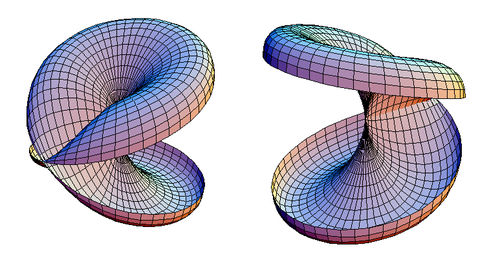Figura 2. Dos vistas de un disco de tapa cruzada que se ha cortado en rodajas.

Una vez que se haga esta excepción, se verá que el disco de corte cruzado segmentado es homeomórfico a un disco de auto-intersección, como se muestra en la Figura 3.

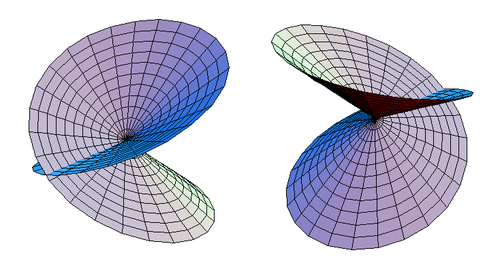Figura 3. Dos vistas alternativas de un disco de auto-intersección.

El disco de auto-intersección es homeomorfo a un disco ordinario. Las ecuaciones paramétricas del disco de auto-intersección son:

$${\ displaystyle X (u, v) = r \, v \, \ cos 2u,}

$${\ displaystyle Y (u, v) = r \, v \, \ sin 2u,}

$${\ displaystyle Z (u, v) = r \, v \, \ cos u,}

donde u varía de 0 a 2 π y v varía de 0 a 1.

Proyectando el disco de auto-intersección en el plano de simetría ( z = 0 en la parametrización dada anteriormente) que pasa solo a través de los puntos dobles, el resultado es un disco ordinario que se repite (se duplica sobre sí mismo).

El plano z = 0 corta el disco de auto-intersección en un par de discos que son reflejos entre sí. Los discos tienen centros en el origen .

Ahora considere los bordes de los discos (con v = 1). Los puntos en el borde del disco de auto-intersección vienen en pares que son reflejos entre sí con respecto al plano z = 0.

Se forma un disco de tapa cruzada identificando estos pares de puntos, haciéndolos equivalentes entre sí. Esto significa que un punto con parámetros ( u , 1) y coordenadas$${\ displaystyle (r \, \ cos 2u, r \, \ sin 2u, r \, \ cos u)}se identifica con el punto ( u + π, 1) cuyas coordenadas son$${\ displaystyle (r \, \ cos 2u, r \, \ sin 2u, -r \, \ cos u)}. Pero esto significa que los pares de puntos opuestos en el borde del disco ordinario (equivalente) se identifican entre sí; Así es como un plano proyectivo real se forma a partir de un disco. Por lo tanto, la superficie mostrada en la Figura 1 (casquillo cruzado con disco) es topológicamente equivalente al plano proyectivo real RP ² .

Coordenadas homogéneas [ editar ]

Artículo principal: Coordenadas homogéneas.

Los puntos en el plano pueden ser representados por coordenadas homogéneas . Un punto tiene coordenadas homogéneas [ x  :  y  :  z ], donde se considera que las coordenadas [ x  :  y  :  z ] y [ tx  :  ty  :  tz ] representan el mismo punto, para todos los valores distintos de cero de t . Los puntos con coordenadas [ x  :  y  : 1] son ​​el plano real usual , llamado la parte finita del plano proyectivo, y los puntos con coordenadas [ x  :  y : 0], llamados puntos en el infinito o puntos ideales , constituyen una línea llamada la línea en el infinito . (Las coordenadas homogéneas [0: 0: 0] no representan ningún punto.)

Las líneas en el plano también se pueden representar mediante coordenadas homogéneas. Una línea proyectiva correspondiente al plano ax + por + cz = 0 en R ³ tiene las coordenadas homogéneas ( a  :  b  :  c ). Por lo tanto, estas coordenadas tienen la relación de equivalencia ( a  :  b  :  c ) = ( da  :  db  :  dc ) para todos los valores distintos de cero de d . De ahí una ecuación diferente de la misma línea dax  +  dby  +  dcz = 0 da las mismas coordenadas homogéneas. Un punto [ x  :  y  :  z ] se encuentra en una línea ( a  :  b  :  c ) si ax  +  by  +  cz  = 0. Por lo tanto, las líneas con coordenadas ( a  :  b  :  c ) donde a ,  b no son ambos 0 corresponden a las líneas en el plano real habitual , porque contienen puntos que no están en el infinito. La línea con coordenadas (0: 0: 1) es la línea en el infinito, ya que los únicos puntos en ella son aquellos con  z  = 0.

Puntos, líneas y planos [ editar ]

Una línea en P ² se puede representar mediante la ecuación ax + by + cz = 0. Si tratamos a , b y c como el vector de columna ℓy x , y , z como el vector de columna x , la ecuación anterior puede ser escrito en forma de matriz como:

x ^T ℓ = 0 o ℓ ^T x = 0.

Usando notación vectorial podemos escribir x ⋅ ℓ = 0 o ℓ ⋅ x = 0.

La ecuación k ( x ^T ℓ ) = 0 (que k es un escalar distinto de cero) barre un plano que pasa por cero en R ³ y k ( x ) barre una línea, nuevamente pasando por cero. El plano y la línea son subespacios lineales en R ³ , que siempre pasan por cero.

Puntos ideales [ editar ]

En P ^2, la ecuación de una línea es ax + by + cz = 0 y esta ecuación puede representar una línea en cualquier plano paralelo al plano x , y multiplicando la ecuación por k .

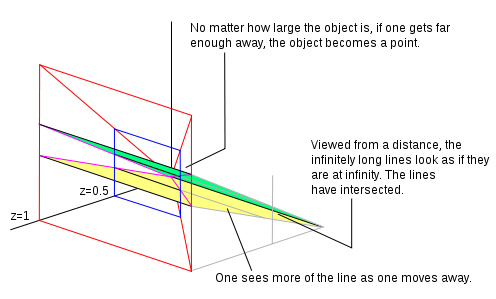
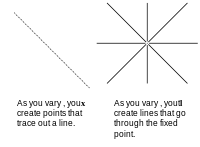
Si z = 1 tenemos una coordenada homogénea normalizada. Todos los puntos que tienen z = 1 crean un plano. Supongamos que estamos mirando ese plano (desde una posición más alejada a lo largo del eje z y mirando hacia el origen) y hay dos líneas paralelas dibujadas en el plano. Desde donde estamos parados (dadas nuestras capacidades visuales) solo podemos ver gran parte del plano, que representamos como el área delineada en rojo en el diagrama. Si nos alejamos del plano a lo largo del eje z , (aún mirando hacia atrás hacia el origen), podemos ver más del plano. En nuestro campo de visión se han movido los puntos originales. Podemos reflejar este movimiento dividiendo la coordenada homogénea por una constante. En la imagen adyacente hemos dividido por 2 para que elEl valor z ahora se convierte en 0.5. Si nos alejamos lo suficiente, lo que estamos viendo se convierte en un punto en la distancia. A medida que nos alejamos, vemos cada vez más líneas paralelas. Las líneas se encontrarán en una línea en el infinito (una línea que pasa por cero en el plano en z = 0). Las líneas en el plano cuando z = 0 son puntos ideales. El plano en z = 0 es la línea en el infinito.

El punto homogéneo (0, 0, 0) es donde van todos los puntos reales cuando miras el plano desde una distancia infinita, una línea en el plano z = 0 es donde las líneas paralelas se intersecan.

La dualidad [ editar ]

En la ecuación x ^T ℓ = 0 hay dos vectores de columnas . Puede mantenerse constante y variar el otro. Si mantenemos el punto x constante y variar los coeficientes ℓ creamos nuevas líneas que pasan por el punto. Si mantenemos los coeficientes constantes y variamos los puntos que satisfacen la ecuación, creamos una línea. Consideramos a x como un punto, porque los ejes que estamos usando son x , y y z . Si en cambio graficamos los coeficientes usando el eje marcado a , b , cLos puntos se convertirían en líneas y las líneas se convertirían en puntos. Si pruebas algo con los datos representados en el eje marcado x , y , y z el mismo argumento se puede utilizar para los datos trazados en el eje marcado un , b , y c . Eso es dualidad.

Líneas que unen puntos e intersección de líneas (usando dualidad) [ editar ]

La ecuación x ^T ℓ = 0 calcula el producto interno de dos vectores de columna. El producto interno de dos vectores es cero si los vectores son ortogonales . En P ² , la línea entre los puntos x ₁ y x ₂ puede representarse como un vector de columna ℓ que satisface las ecuaciones x ₁ ^T ℓ = 0 y x ₂ ^T ℓ = 0, o en otras palabras, un vector de columna ℓ que es ortogonal a x ₁ y x ₂ . losEl producto cruzado encontrará un vector de este tipo: la línea que une dos puntos tiene coordenadas homogéneas dadas por la ecuación x ₁ × x ₂ . La intersección de dos líneas se puede encontrar de la misma manera, utilizando la dualidad, como el producto cruzado de los vectores que representan las líneas, ℓ ₁ × ℓ ₂ .

Incrustación en el espacio de 4 dimensiones [ editar ]

El plano proyectivo se incrusta en el espacio euclidiano en 4 dimensiones. El plano proyectivo real P ² ( R ) es el cociente de la esfera doble.

S ² = {( x , y , z ) ∈ R ³  : x ² + y ² + z ² = 1}

por la relación antípoda ( x , y , z ) ~ (- x , - y , - z ). Considere la función R ³ → R ⁴ dada por ( x , y , z ) ↦ ( xy , xz, y ² - z ² , 2 yz ). Este mapa se restringe a un mapa cuyo dominio es S ² y, dado que cada componente es un polinomio homogéneo de grado uniforme, toma los mismos valores en R ⁴en cada uno de los dos puntos antípodas en S ² . Esto produce un mapa P ² ( R ) → R ⁴ . Además, este mapa es una incrustación. Tenga en cuenta que esta incrustación admite una proyección en R ^3, que es la superficie romana .

Superficies no orientables más altas [ editar ]

Al pegar planos proyectivos sucesivamente obtenemos superficies no orientables de demigenus superiores . El proceso de encolado consiste en cortar un pequeño disco de cada superficie e identificar ( encolar ) sus círculos de contorno. Pegando dos planos proyectivos crea la botella de Klein .

El artículo sobre el polígono fundamental describe las superficies no orientables más altas.