FORMAS GEOMÉTRICAS - SUPERFICIES

 montura del mono es la superficiedefinida por la ecuación.

$${\ displaystyle z = x ^ {3} -3xy ^ {2}. \,}

Pertenece a la clase de superficies de silla de montar , y su nombre deriva de la observación de que una silla de montarpara un mono requeriría tres depresiones: dos para las piernas y una para la cola. El punto (0,0,0) en la montura del mono corresponde a un punto crítico degenerado de la función z ( x , y ) en (0, 0). La montura del mono tiene un punto umbilical aislado con cero curvatura gaussiana en el origen, mientras que la curvatura es estrictamente negativa en todos los demás puntos.

Para mostrar que la montura del mono tiene tres depresiones, se puede escribir la ecuación para z usando números complejos como ^[1]

$${\ displaystyle z (x, y) = \ operatorname {Re} [(x + iy) ^ {3}].}

De ello se deduce que z ( tx , ty ) = t ³ z ( x , y ) para t ≥ 0 , por lo que la superficie está determinada por z en el círculo unitario . Parametrizando esto por e ^iφ , con φ ∈ [0, 2π] , se puede ver que en el círculo unitario, z ( φ ) = cos 3 φ , entonces z tiene tres depresiones. Al reemplazar 3 con cualquier entero k ≥ 1 , se puede crear una silla con k depresiones.

Otro ejemplo de la montura del mono es el pétalo fundido definido por la ecuación.$${\ displaystyle x + y + z + xyz = 0}.

La montura del mono

Fundir el pétalo $${\ displaystyle x + y + z + xyz = 0}

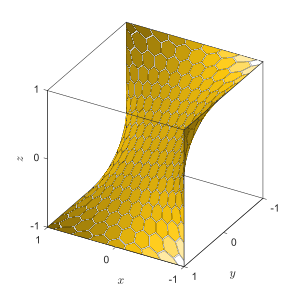
El término silla de caballo se utiliza, en contraste con mono silla de montar, para designar un punto de silla de montarque es un minimax , es decir, un mínimo o máximo local en función del plano de intersección utilizado. La montura de mono tiene solo un punto de inflexión . Para ver esto, considere una línea y = kx . En esta dirección, la superficie se convierte simplemente en z = (1 - 3 k ² ) x ³ , sin puntos críticos .

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Superficie de morin vista desde la parte superior.

Superficie de morin vista desde el lateral.

La superficie de Morin es el modelo a medio camino de la eversión de esfera descubierta por Bernard Morin . Cuenta con cuatro simetríarotacional .

Si la esfera original a volverse tiene su superficie exterior de color verde y su superficie interior de color rojo, entonces cuando la esfera se transforme a través de homotopy en una superficie de Morin, la mitad de la superficie de Morin visible hacia el exterior será verde y la mitad roja:

La mitad de la superficie de Morin corresponde al exterior (verde) de la esfera 
en la que se encuentra homeomorfo, y la otra mitad simétrica al interior (rojo).

Luego, al rotar la superficie 90 ° alrededor de su eje de simetría, se intercambiarán sus colores, es decir, se cambiará la polaridad interior-exterior de la superficie orientable, de modo que el retroceso de los pasos de la homotopía exactamente en la misma posición de vuelta a la esfera original después de haber así rotada, la superficie Morin producirá una esfera cuya superficie exterior es roja y cuya superficie interna es verde: una esfera que se ha vuelto del revés. El siguiente es un resumen de la eversión:

1. esfera: verde exterior, rojo interior ... 
2. se transforma en ... 
3. Superficie de Morin, 
3 '. Superficie de Morin rotada 90 ° ... 
2 '. Se transforma inversamente en ... 
1 '. esfera: rojo por fuera, verde por dentro.

Estructura de la superficie Morin [ editar ]

La superficie de Morin se puede separar en cuatro secciones congruentes. Estas secciones pueden denominarse aquí Sección este, sección Sur, sección Oeste y sección Norte, o respectivamente, sección 0, sección 1, sección 2 y sección 3.

Sección este de la superficie Morin.

La superficie de Morin tiene un punto cuádruple a través del cual pasa su eje de simetría. Este punto cuádruple es el punto inicial y el punto final de seis líneas de puntos dobles. Cada una de las secciones de cuartos está delimitada por tres de estas líneas de puntos dobles, de modo que cada sección de cuartos es homeomórfica a un triángulo. La sección Este ahora se muestra esquemáticamente: El diagrama muestra la sección Este delimitada por tres bucles: ABCDA, AEFGA y AHIJA. El tercer bucle, AHIJA, es una línea de puntos dobles donde la sección Este se cruza consigo misma. Loop ABCDA es solo una línea de puntos dobles cuando la sección Este está unida a la sección Oeste, y el bucle AEFGA es solo una línea de puntos dobles cuando la sección Este está unida a la sección Sur. Punto es el punto cuádruple que en realidad es la superposición de cuatro puntos diferentes: A ₀ , A

₁ , A ₂ , A ₃ .

Así es como la sección Este se une a las otras secciones: permita que cada uno de sus bucles delimitadores se especifique mediante una quintuplicada ordenada de puntos, luego

$${\ displaystyle (A_ {1}, B, C, D, A_ {3}) = (A_ {1}, D '', C '', B '', A_ {3})}

$${\ displaystyle (A_ {2}, E, F, G, A_ {3}) = (A_ {2}, H ', I', J ', A_ {3})}

$${\ displaystyle (A_ {1}, H, I, J, A_ {2}) = (A_ {1}, E '' ', F' '', G '' ', A_ {2})}

donde los puntos no imprimados pertenecen a la sección 0 (Este), los puntos imprimados pertenecen a la sección 1 (Sur), los puntos de imprimación doble pertenecen a la sección 2 (Oeste) y los puntos de imprimación triple pertenecen a la sección 3 (Norte).

Los tres bucles restantes conectan las secciones de la siguiente manera:

$${\ displaystyle (A_ {2}, B ', C', D ', A_ {0}) = (A_ {2}, D' '', C '' ', B' '', A_ {0}) }

$${\ displaystyle (A_ {3}, E ', F', G ', A_ {0}) = (A_ {3}, H' ', I' ', J' ', A_ {0})}

$${\ displaystyle (A_ {0}, E '', F '', G '', A_ {1}) = (A_ {0}, H '' ', I' '', J '' ', A_ { 1}).}

La sección Este tiene, considerada solo por sí misma, un bucle de puntos dobles: AHIJA. Si la superficie se desenrolla y se aplana, el resultado será el siguiente: que es homeomorfo a un triángulo:

Unir las cuatro secciones triangulares en sus costuras producirá un tetraedro : que es homeomorfo a una esfera, que muestra que la superficie de Morin es una esfera de auto-intersección. 

Galería de superficie Morin [ editar ]

Cuatro vistas diferentes de la superficie de Morin: las dos primeras se muestran con "barreras de paso" recortadas, las dos últimas son vistas desde el "fondo".

Morin analítica superficie [ editar ]

La superficie de Morin puede describirse con elegancia mediante un conjunto de ecuaciones ^[1] en versión abierta (con polos enviados al infinito) o cerrada.

 globo de mylar es una superficie de revolución . Mientras que una esfera es la superficie que encierra un volumen máximo para un área de superficie dada , el globo de mylar en su lugar maximiza el volumen para una longitud de arco de generatriz determinada . Se asemeja a una esfera ligeramente aplanada.

La forma se realiza aproximadamente al inflar un globo físico hecho de dos láminas circulares de material flexible e inelástico; por ejemplo, un tipo popular de globo de juguete hecho de plástico aluminizado . Quizás contraintuitivamente, el área de superficie del globo inflado es menor que el área de superficie de las hojas circulares. Esto se debe a la ondulación física de la superficie, que aumenta cerca del borde.

"Globo de Mylar" es el nombre de la figura dada por W. Paulson, quien primero investigó la forma. El término fue posteriormente adoptado por otros escritores. "Mylar" es una marca registrada de DuPont .

Definición [ editar ]

La parte positiva de la generatriz del globo es la función z ( x ) donde para una longitud de generatriz dada a :

$${\ displaystyle z (r) = 0}

$${\ displaystyle \ int _ {0} ^ {r} \! {\ sqrt {1 + z '(x) ^ {2}}} \, dx \, = a} (es decir, se da la longitud de la generatriz)

$${\ displaystyle \ int _ {0} ^ {r} \! 4 \ pi xz (x) \, dx} es un máximo (es decir, el volumen es máximo)

Aquí, el radio r se determina a partir de las restricciones.

Caracterización paramétrica [ editar ]

Las ecuaciones paramétricas para la generatriz de un globo de radio r están dadas por:

$${\ displaystyle x (u) = r \ cos u; \ qquad z (u) = r {\ sqrt {2}} \ left [E (u, {\ frac {1} {\ sqrt {2}}}) - {\ frac {1} {2}} F (u, {\ frac {1} {\ sqrt {2}}}) \ right] {\ text {for}} u \ in [0, {\ frac { \ pi} {2}}] \,}

(donde E y F son integrales elípticas del segundo y primer tipo)

Medición [ editar ]

El "espesor" τ del globo (es decir, la distancia a través del eje de rotación) se puede determinar calculando $${\ displaystyle 2z ({\ frac {\ pi} {2}})}a partir de las ecuaciones paramétricas anteriores. El espesor es de aproximadamente

τ ≈ 0.599 · 2 r .

La relación de τ a r es independiente del tamaño del globo.

La relación entre la longitud de arco de la generatriz y el radio del globo es aproximadamente

a / r ≈ 1.3110. (La referencia indica que "a" es el radio del globo desinflado, "r" es el radio del globo inflado)

El volumen del globo está dado por:

$${\ displaystyle V = {\ frac {2} {3}} \ pi ar ^ {2},}

donde a es la longitud del arco de la generatriz).

o alternativamente:

$${\ displaystyle V = {\ frac {4} {3}} \ tau a ^ {2},}

donde τ es el espesor en el eje de rotación

Geometría de la superficie [ editar ]

La relación de las curvaturas principales en cada punto del globo mylar es exactamente 2, lo que lo convierte en un caso interesante de una superficie de Weingarten . Por otra parte, esta única propiedad caracteriza completamente el globo. El globo es evidentemente más plano en el eje de rotación; Este punto es en realidad tiene una curvatura cero en cualquier dirección.