La cinta de Möbius o banda de Möbius ( UK : / m ɜː b i ə s / , Estados Unidos : / m oʊ
Se puede crear un ejemplo de una tira de Möbius tomando una tira de papel y dándole medio giro, y luego uniendo los extremos de la tira para formar un bucle. Sin embargo, la tira de Möbius no es una superficie de solo un tamaño y forma exactos, como la tira de papel medio torcida que se muestra en la ilustración. Más bien, los matemáticos se refieren a la banda cerrada de Möbius como cualquier superficie que sea homeomórfica en esta tira. Su límite es una curva cerrada simple, es decir, homeomorfo a un círculo. Esto permite una gran variedad de versiones geométricas de la banda de Möbius como superficies, cada una con un tamaño y forma definidos. Por ejemplo, cualquier rectángulo se puede pegar a sí mismo (identificando un borde con el borde opuesto después de una inversión de orientación) para hacer una banda de Möbius. Algunos de estos pueden ser modelados sin problemas enEspacio euclidiano , y otros no pueden.
Una media vuelta en el sentido de las agujas del reloj proporciona una inserción de la tira de Möbius diferente a la de una media vuelta en el sentido contrario a las agujas del reloj, es decir, como un objeto incrustado en el espacio euclidiano, la tira de Möbius es un objeto quiralcon diestros o zurdos. Sin embargo, los espacios topológicossubyacentes.Dentro de la franja de Möbius son homeomorfos en cada caso. Existe un número infinito de incrustaciones topológicamente diferentes del mismo espacio topológico en el espacio tridimensional, ya que la tira de Möbius también se puede formar torciendo la tira un número impar de veces mayor que uno, o anudando y girando la tira, antes de unirla envía. La banda de Möbius abierta completa es un ejemplo de una superficie topológica que está estrechamente relacionada con la banda de Möbius estándar, pero que no es homeomórfica.
Encontrar ecuaciones algebraicas , cuyas soluciones tienen la topología de una tira de Möbius, es sencillo, pero, en general, estas ecuaciones no describen la misma forma geométrica que se obtiene del modelo de papel torcido descrito anteriormente. En particular, el modelo de papel torcido es una superficie desarrollable , con una curvatura gaussiana cero . Un sistema de ecuaciones algebraicas diferenciales que describe modelos de este tipo se publicó en 2007 junto con su solución numérica. [6]
Propiedades [ editar ]
La tira de Möbius tiene varias propiedades curiosas. Una línea dibujada a partir de la costura por la mitad se encuentra en la costura, pero en el otro lado. Si continúa, la línea cumple con el punto de inicio y es el doble de la longitud de la tira original. Esta única curva continua demuestra que la banda de Möbius tiene un solo límite .
Cortar una tira de Möbius a lo largo de la línea central con un par de tijeras produce una tira larga con dos giros completos, en lugar de dos tiras separadas; El resultado no es una tira de Möbius. Esto sucede porque la tira original solo tiene un borde que es dos veces más largo que la tira original. El corte crea un segundo borde independiente, la mitad del cual estaba en cada lado de las tijeras. Cortar esta nueva, más larga, tira por el medio crea dos tiras enrolladas entre sí, cada una con dos giros completos.
Si la tira se corta a lo largo de aproximadamente un tercio del borde, crea dos tiras: una es una tira de Möbius más delgada: es el tercio central de la tira original, que comprende un tercio del ancho y la misma longitud como la tira original. La otra es una tira más larga pero delgada con dos giros completos en ella: es una zona adyacente al borde de la tira original, y comprende un tercio del ancho y el doble de la longitud de la tira original.
Se pueden obtener otras tiras análogas al unir tiras similares con dos o más giros medios en ellas en lugar de uno. Por ejemplo, una tira con tres medias torsiones, cuando se divide longitudinalmente, se convierte en una tira torcida atada en un nudo de trébol . (Si este nudo se desenreda, la tira tiene ocho semi-giros). Una tira con Nsemi-giros, cuando se divide, se convierte en una tira con N + 1 giros completos. Darle giros adicionales y volver a conectar los extremos produce figuras llamadas anillos paradómicos .
La geometría y la topología [ editar ]
Una forma de representar la tira de Möbius como un subconjunto del espacio euclidiano tridimensional es mediante la parametrización:
dónde y . Esto crea una tira de Möbius de ancho 1 cuyo círculo central tiene un radio de 1, se encuentra en elplano y se centra en . El parámetro corre alrededor de la tira mientras Se mueve de un borde al otro.
En coordenadas polares cilíndricas. , una versión ilimitada de la tira de Möbius se puede representar mediante la ecuación:
La inserción isométrica más amplia en 3 espacios [ editar ]
Si una tira de Möbius lisa en tres espacios es rectangular, es decir, creada a partir de la identificación de dos lados opuestos de un rectángulo geométrico con flexión pero sin estirar la superficie, se sabe que tal incrustación es posible si la relación de aspecto del El rectángulo es mayor que la raíz cuadrada de tres. (Tenga en cuenta que los lados más cortos del rectángulo se identifican para obtener la tira de Möbius). Para una relación de aspecto menor o igual a la raíz cuadrada de tres, sin embargo, una incrustación suave de una tira de Möbius rectangular en tres espacios puede ser imposible.
A medida que la relación de aspecto se aproxima a la relación límite de √ 3 desde arriba, cualquier tira de Möbius rectangular en tres espacios parece aproximarse a una forma que en el límite se puede considerar como una tira de tres triángulos equiláteros, doblados uno encima del otro de modo que ocupen un solo triángulo equilátero en tres espacios.
Sin embargo, si la tira de Möbius en tres espacios es solo una vez continuamente diferenciable (en símbolos: C 1 ), entonces el teorema de Nash-Kuiper muestra que no existe un límite inferior.
Un método para hacer una tira de Möbius a partir de una tira rectangular demasiado ancha para simplemente torcerla y unirla (por ejemplo, un rectángulo de solo una unidad de largo y otra de ancho) es doblar primero la dirección ancha de un lado a otro utilizando un número par de pliegues: un "pliegue de acordeón": para que la tira plegada se vuelva lo suficientemente estrecha como para poder torcerla y unirla, al igual que una sola tira suficientemente larga. [7]Con dos pliegues, por ejemplo, una tira de 1 × 1 se convertiría en una tira plegada de 1 × whose cuya sección transversaltiene la forma de una 'N' y seguiría siendo una 'N' después de un medio giro. Esta tira doblada, tres veces más larga que ancha, sería lo suficientemente larga como para unirse en los extremos. Este método funciona en principio, pero se vuelve poco práctico después de suficientes pliegues, si se usa papel. Al usar papel normal, esta construcción se puede plegar plana , con todas las capas del papel en un solo plano, pero matemáticamente, no está claro si esto es posible sin estirar la superficie del rectángulo. [8]
Topologia [ editar ]
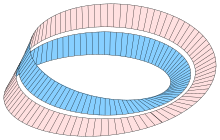
Topológicamente , la tira de Möbius se puede definir como el cuadrado Con sus lados superior e inferior identificados por la relación. para , como en el diagrama de la derecha.
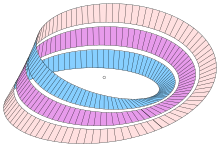
Una presentación menos utilizada de la tira de Möbius es como el cociente topológico de un toro. [9] Un toro puede ser construido como el cuadrado. con los bordes identificados como (pegar de izquierda a derecha) y (pegar de abajo hacia arriba). Si uno también identificó ( x , y ) ~ ( y , x ) , entonces uno obtiene la tira de Möbius. La diagonal del cuadrado (los puntos ( x , x ) donde ambas coordenadas coinciden) se convierte en el límite de la tira de Möbius, y lleva una estructura de orbifold, que corresponde geométricamente a "reflexión": geodésicas (líneas rectas) en la tira de Möbius refleja fuera del borde de nuevo en la tira. Notacionalmente, esto se escribe como T 2 / S 2 - el toro 2 cocido por la acción de grupo del grupo simétricoen dos letras (coordenadas de cambio), y puede considerarse como el espacio de configuración de dos puntos desordenados en el círculo, posiblemente el mismo (el borde corresponde a los puntos que son iguales), con el toro correspondiente a dos puntos ordenados en el círculo.
La tira de Möbius es una variedad compacta bidimensional (es decir, una superficie ) con borde. Es un ejemplo estándar de una superficie que no es orientable . De hecho, la tira de Möbius es el epítome del fenómeno topológico de la no orientación . Esto se debe a que las formas bidimensionales (superficies) son las formas de dimensiones más bajas para las cuales es posible la no orientación y la tira de Möbius es la única superficie que es topológicamente un subespacio de cada superficie no orientable. Como resultado, cualquier superficie no se puede orientar si y solo si contiene una banda de Möbius como un subespacio.
La tira de Möbius es también un ejemplo estándar utilizado para ilustrar el concepto matemático de un paquete de fibra . Específicamente, es un paquete no trivial sobre el círculo S 1 con una fibra del intervalo de la unidad , I = [0, 1] . Al mirar solo el borde de la tira de Möbius se obtiene un haz de dos puntos (o Z 2 ) no trivial sobre S 1 .
Gráficos por computadora [ editar ]
Una construcción simple de la tira de Möbius que se puede usar para representarla en gráficos de computadora o paquetes de modelado es:
- Toma una tira rectangular. Gírelo alrededor de un punto fijo que no esté en su plano. En cada paso, también gire la tira a lo largo de una línea en su plano (la línea que divide la tira en dos) y perpendicular al radio orbital principal. La superficie generada en una revolución completa es la tira de Möbius.
- Toma una tira de Möbius y córtala en el centro de la tira. Esto forma una nueva franja, que es un rectángulo unido al rotar un extremo por todo un turno. Al cortarlo por la mitad nuevamente, esto forma dos tiras de giro completo entrelazadas.
Abrir la banda de Möbius [ editar ]
La banda abierta de Möbius se forma al eliminar el límite de la banda estándar de Möbius. Se construye a partir del conjunto S = {( x , y ) ∈ R 2 : 0 ≤ x ≤ 1 y 0 < y <1 font=""> identificando (pegando) los puntos (0, y ) y (1, 1 - y ) para todos 0 < y <1 font=""> .
Puede construirse como una superficie de curvatura constante positiva, negativa o cero (gaussiana) . En los casos de curvatura negativa y cero, la banda de Möbius puede construirse como una superficie completa (geodésicamente), lo que significa que todas las geodésicas ("líneas rectas" en la superficie) pueden extenderse indefinidamente en cualquier dirección.
Curvatura negativa constante: al igual que el plano y el cilindro abierto, la banda abierta de Möbius admite no solo una métrica completa de curvatura constante 0, sino también una métrica completa de curvatura negativa constante, por ejemplo, -1. Una forma de ver esto es comenzar con el modelo del plano hiperbólico half del plano medio superior (Poincaré) , es decir, ℍ = {( x , y ) ∈ ℝ 2 | y > 0} con la métrica riemanniana dada por ( dx 2 + dy 2 ) / y 2 . Las isometrías que preservan la orientación de esta métrica son todos los mapas f : ℍ → ℍde la forma f ( z ): = ( az + b ) / ( cz + d ) , donde a , b , c , d son números reales que satisfacen ad - bc = 1 . Aquí z es un número complejo con Im ( z )> 0 , y hemos identificado ℍ con { z ∈ ℂ | Im ( z )> 0} dotado con la métrica de Riemann que se mencionó. Entonces una isometría de inversión de orientación g de ℍ dada porg ( z ): = -conj ( z ) , donde conj ( z ) denota el complejo conjugado de z . Estos hechos implican que el mapeoh : ℍ → ℍ dado por h ( z ): = −2⋅conj ( z ) es una isometría de inversión de orientación de ℍ que genera un grupo cíclico infinito G de isometrías. (Su cuadrado es la isometría h ( z ): = 4⋅z , que se puede expresar como( 2z + 0 ) / ( 0z + 1/2 ) .) El cociente ℍ /G de la acción de este grupo puede verse fácilmente como topológicamente una banda de Möbius. Pero también es fácil verificar que esté completo y no sea compacto, con una curvatura negativa constante −1.
El grupo de isometrías de esta banda de Möbius es unidimensional y es isomorfo al grupo ortogonal especial SO (2).
Curvatura cero (constante): también se puede construir como una superficie completa, comenzando con la porción del plano R 2 definida por 0 ≤ y ≤ 1 e identificando ( x , 0) con (- x , 1) para todas las x en R (los reales). La métrica resultante convierte a la banda de Möbius abierta en una superficie plana (geodésicamente) completa (es decir, con una curvatura gaussiana igual a 0 en todas partes). Esta es la única métrica en la banda de Möbius, hasta una escala uniforme, que es plana y completa.
El grupo de isometrías de esta banda de Möbius es unidimensional y es isomorfo al grupo ortogonal SO (2).
Curvatura positiva constante: una banda de Möbius de curvatura positiva constante no se puede completar, ya que se sabe que las únicas superficies completas de curvatura positiva constante son la esfera y el plano proyectivo . El plano proyectivo P 2 de curvatura constante +1 puede construirse como el cociente de la esfera unitaria S 2 en R 3 mediante el mapa antípodas A : S 2 → S 2 , definido por A ( x , y , z ) = (- x , - y , - z ). La banda de Möbius abierta es homeomórfica al plano proyectivo una vez perforado, es decir, P 2 con cualquier punto eliminado. Puede pensarse que esto es lo más cerca que una banda de Möbius de curvatura positiva constante puede llegar a ser una superficie completa: a un punto de distancia.
El grupo de isometrías de esta banda de Möbius también es unidimensional e isomorfo al grupo ortogonal O (2).
El espacio de las líneas no orientadas en el plano es difeomorfo a la banda de Möbius abierta. [10] Para ver por qué, vamos a L ( θ ) denotar la línea a través del origen en un ángulo θ al eje x positivo. Para cada L ( θ ) no es la familia P ( θ ) de todas las líneas en el plano que son perpendiculares a L ( θ ). Topológicamente, la familia P ( θ ) es solo una línea (porque cada línea en P ( θ ) intersecta la línea L ( θ)) en un solo punto). De esta manera, a medida que θ aumenta en el rango 0 ° ≤ θ <180 font=""> , la línea L ( θ ) representa el valor de una línea de líneas distintas en el plano. Pero cuando θ alcanza 180 °, L (180 °) es idéntico a L (0), por lo que las familias P (0 °) y P(180 °) de las líneas perpendiculares también son familias idénticas. Sin embargo, la línea L (0 °) se ha vuelto a sí misma como L (180 °) apuntada en la dirección opuesta . Cada línea en el plano corresponde exactamente a una línea en alguna familia P ( θ), para exactamente un θ , para 0 ° ≤ θ <180 font=""> , y P (180 °) es idéntico a P (0 °) pero regresa apuntado en la dirección opuesta. Esto asegura que el espacio de todas las líneas en el plano - la unión de todo el L ( θ ) para 0 ° ≤ θ ≤ 180 ° - es una banda de Möbius abierta.
El grupo de transformaciones lineales biyectivas GL (2, R ) del plano a sí mismo ( matrices reales 2 × 2 con determinante distinto de cero) naturalmente induce bijections del espacio de líneas en el plano a sí mismo, que forman un grupo de self- Homeomorfismos del espacio de líneas. Por lo tanto, el mismo grupo forma un grupo de auto-homeomorfismos de la banda de Möbius descrito en el párrafo anterior. Pero no hay métrica sobre el espacio de líneas en el plano que es invariante bajo la acción de este grupo de homeomorfismos. En este sentido, el espacio de líneas en el plano no tiene una métrica natural.
Esto significa que la banda de Möbius posee un grupo natural de mentiras en 4 dimensiones de auto-homeomorfismos, dado por GL (2, R ) , pero este alto grado de simetría no puede mostrarse como el grupo de isometrías de cualquier métrica.
Banda de Möbius con límite redondo [ editar ]
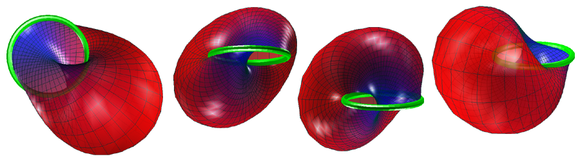
El borde o límite de una tira de Möbius es homeomorfo (topológicamente equivalente) a un círculo . Bajo las incrustaciones habituales de la franja en el espacio euclidiano, como arriba, el límite no es un círculo verdadero. Sin embargo, es posible incrustar una tira de Möbius en tres dimensiones para que el límite sea un círculo perfecto que se encuentra en algún plano. Por ejemplo, vea las Figuras 307, 308 y 309 de "Geometría y la imaginación". [11]
Una incrustación mucho más geométrica comienza con una mínima botella de Klein inmersa en la esfera 3, como descubrió Blaine Lawson. Luego tomamos la mitad de esta botella de Klein para incrustar una banda de Möbius en la esfera 3 (la esfera unidad en el espacio 4). El resultado a veces se llama "Banda de Möbius de Sudán", [12]donde "sudanés" se refiere no a Sudán del país, sino a los nombres de dos topólogos, Sue Goodman y Daniel Asimov. La aplicación de la proyección estereográfica a la banda sudanesa lo coloca en un espacio tridimensional, como se puede ver a continuación . Aquí se puede encontrar una versión de George Francis .
De la botella Klein mínima de Lawson derivamos una inserción de la banda en la S 3 de 3 esferas , considerada como un subconjunto de C 2 , que geométricamente es lo mismo que R 4 . Mapeamos ángulos η , φ a números complejos z 1 , z 2 a través de
Aquí el parámetro η se ejecuta de 0 a π y φ se ejecuta de 0 a 2 π . Desde | z 1 | 2 + | z 2 | 2 = 1 , la superficie incrustada se encuentra completamente en S 3 . El límite de la tira está dado por | z 2 | = 1 (correspondiente a η = 0, π ), que es claramente un círculo en la esfera 3.
Para obtener una incrustación de la tira de Möbius en R 3, se mapea S 3 a R 3 mediante una proyección estereográfica . El punto de proyección puede ser cualquier punto en S 3 que no se encuentre en la tira de Möbius incrustada (esto excluye todos los puntos de proyección habituales). Una posible opción es. Las proyecciones estereográficas trazan círculos en círculos y preservan el límite circular de la tira. El resultado es una integración suave de la banda de Möbius en R 3 con un borde circular y sin auto-intersecciones.
La banda de Möbius de Sudán en la S- 3 de tres esferas es geométricamente un haz de fibras sobre un gran círculo, cuyas fibras son grandes semicírculos. La imagen más simétrica de una proyección estereográfica de esta banda en R 3 se obtiene utilizando un punto de proyección que se encuentra en ese gran círculo que se extiende a través del punto medio de cada uno de los semicírculos. Cada elección de tal punto de proyección resulta en una imagen que es congruente con cualquier otra. Pero como tal punto de proyección se encuentra en la propia banda de Möbius, dos aspectos de la imagen son significativamente diferentes del caso (ilustrado arriba) donde el punto no está en la banda: 1) la imagen en R 3no es la banda completa de Möbius, sino la banda con un punto eliminado (de su línea central); y 2) la imagen es ilimitada y, a medida que se aleja cada vez más del origen de R 3 , se aproxima cada vez más a un plano. Sin embargo, esta versión de la imagen estereográfica tiene un grupo de 4 simetrías en R 3 (es isomorfa al grupo 4 de Klein ), en comparación con la versión acotada ilustrada anteriormente que tiene su grupo de simetrías el grupo único de orden 2. (Si se permiten todas las simetrías y no solo las isometrías de R 3 que conservan la orientación , el número de simetrías en cada caso se duplica.
Pero la versión más geométricamente simétrica de todos es la banda original de Sudán Möbius en los tres-esfera S 3 , donde su pleno grupo de simetrías es isomorfo al grupo de Lie O (2). Teniendo una cardinalidad infinita (la del continuo ), esto es mucho más grande que el grupo de simetría de cualquier posible incrustación de la banda de Möbius en R 3 .
Objetos relacionados [ editar ]
Un objeto geométrico "extraño" estrechamente relacionado es la botella de Klein . Se puede producir una botella Klein pegando dos tiras de Möbius a lo largo de sus bordes; Esto no se puede hacer en el espacio euclidianotridimensional ordinario sin crear auto-intersecciones. [13]
Otra variedad estrechamente relacionada es el plano proyectivo real . Si un disco circular se corta fuera del plano proyectivo real, lo que queda es una tira de Möbius. [14] Yendo en la otra dirección, si uno pega un disco a una tira de Möbius identificando sus límites, el resultado es el plano proyectivo. Para visualizar esto, es útil deformar la tira de Möbius para que su límite sea un círculo ordinario (ver arriba). El plano proyectivo real, como la botella de Klein, no se puede incrustar en tres dimensiones sin auto-intersecciones.
En teoría de gráficos , la escala de Möbius es un gráfico cúbico estrechamente relacionado con la tira de Möbius.
En 1968, Gonzalo Vélez Jahn (UCV, Caracas, Venezuela) descubrió cuerpos tridimensionales con características möbianas; [15] estos fueron descritos más tarde por Martin Gardner como anillos prismáticos que se convirtieron en poliedros toroidales en su columna de Juegos matemáticos de agosto de 1978 en Scientific American. [dieciséis]
Aplicaciones [ editar ]
Ha habido varias aplicaciones técnicas para la tira de Möbius. Las bandas gigantes de Möbius se han utilizado como cintas transportadoras que duran más porque toda el área de la superficie de la banda tiene la misma cantidad de desgaste, y como cintas de grabación de bucle continuo (para duplicar el tiempo de reproducción). Las tiras de Möbius son comunes en la fabricación de impresoras de tela para computadora y cintas para máquinas de escribir , ya que permiten que la cinta tenga el doble de ancho que el cabezal de impresión al usar ambas mitades de manera uniforme. [17]
Una resistencia de Möbius es un elemento de circuito electrónico que cancela su propia reactancia inductiva. Nikola Tesla patentó una tecnología similar en 1894: [18] "Coil for Electro Magnets" fue diseñada para usarse con su sistema de transmisión global de electricidad sin cables.
La tira de Möbius es el espacio de configuración de dos puntos desordenados en un círculo. En consecuencia, en teoría musical , el espacio de todos los acordes de dos notas, conocidos como díadas , toma la forma de una tira de Möbius; Esto y generalizaciones a más puntos es una aplicación significativa de los orbifolds a la teoría musical . [19] [20]
- Un resonador compacto con una frecuencia de resonancia que es la mitad de las bobinas lineales construidas de manera idéntica [21]
- Una resistencia sin inducción [22]
- Superconductores con alta temperatura de transición [23]
- Resonador de Möbius [24]
- Nudos moleculares con características especiales (Knotane [2], quiralidad)
- Motores moleculares [25]
- Volumen de grafeno (nano-grafito) con nuevas características electrónicas, como el magnetismo helicoidal [26]
- Un tipo especial de aromaticidad: la aromaticidad de Möbius.
- Partículas cargadas atrapadas en el campo magnético de la tierra que pueden moverse en una banda de Möbius
- El ciclótido (proteína cíclica) kalata B1, sustancia activa de la planta Oldenlandia affinis , contiene la topología de Möbius para el esqueleto peptídico.
En la etapa mágica [ editar ]
El principio de la tira de Möbius se ha utilizado como un método para crear la ilusión de la magia . El truco, conocido como las bandas afganas, fue muy popular en la primera mitad del siglo XX. Muchas versiones de este truco existen y han sido realizadas por famosos ilusionistas como Harry Blackstone Sr. y Thomas Nelson Downs .

















![{\ displaystyle [0,1] \ times [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92f35a051af39d8299688d7c4a63e39ee5f95c8b)








No hay comentarios:
Publicar un comentario