LISTA DE TEMAS MATEMÁTICOS - ÁLGEBRA ABSTRACTA

 grupo dicíclico (notación Dic _n o Q _4n ^[1] ) es un miembro de una clase de grupos no abelianos de orden 4 n ( n  > 1). Es una extensión del grupo cíclico de orden 2 por un grupo cíclico de orden 2 n , que da el nombre di-cíclico . En la notación de secuencias exactas de grupos, esta extensión se puede expresar como:

$${\ displaystyle 1 \ a C_ {2n} \ a {\ mbox {Dic}} _ {n} \ a C_ {2} \ a 1. \,}

Más generalmente, dado cualquier grupo abeliano finito con un elemento orden-2, se puede definir un grupo dicíclico.

Definición [ editar ]

Para cada entero n > 1, el grupo dicíclico Dic _n puede definirse como el subgrupo de los cuaterniones unitarios generados por

{\ displaystyle {\ begin {alineado} a & = e ^ {i \ pi / n} = \ cos {\ frac {\ pi} {n}} + i \ sin {\ frac {\ pi} {n}} \ \ x & = j \ end {alineado}}}

De manera más abstracta, se puede definir el grupo dicíclico Dic _n como el grupo con la siguiente presentación ^[2]

$${\ displaystyle {\ mbox {Dic}} _ {n} = \ langle a, x \ mid a ^ {2n} = 1, \ x ^ {2} = a ^ {n}, \ x ^ {- 1} ax = a ^ {- 1} \ rangle. \, \!}

Algunas cosas a tener en cuenta que siguen de esta definición:

• x ⁴ = 1
• x ² a ^k = a ^k + n = a ^k x ²
• si j = ± 1, entonces x ^j a ^k = a ^- k x ^j .
• a ^k x ⁻¹ = a ^k - n a ⁿ x ⁻¹ = a ^k - n x ² x ⁻¹ = a ^k - n x .

Por lo tanto, cada elemento de Dic _n puede escribirse de manera única como una ^k x ^j , donde 0 ≤ k <2 font="" nbsp="">n y j = 0 o 1. La multiplicación reglas están dadas por

• $${\ displaystyle a ^ {k} a ^ {m} = a ^ {k + m}}
• $${\ displaystyle a ^ {k} a ^ {m} x = a ^ {k + m} x}
• $${\ displaystyle a ^ {k} xa ^ {m} = a ^ {km} x}
• $${\ displaystyle a ^ {k} xa ^ {m} x = a ^ {k-m + n}}

De ello se deduce que Dic _n tiene orden 4 n . ^[2]

Cuando n = 2, el grupo dicíclico es isomorfo al grupo cuaternión Q . Más generalmente, cuando n es una potencia de 2, el grupo dicíclico es isomorfo al grupo cuaternión generalizado . ^[2]

Propiedades [ editar ]

Para cada n > 1, el grupo dicíclico Dic _n es un grupo no abeliano de orden 4 n . ("Dic ₁ " es C ₄ , el grupo cíclico de orden 4, que es abeliano, y no se considera dicíclico).

Deje que A = ⟨ un ⟩ el subgrupo de Dic _n generada por una . Entonces A es un grupo cíclico de orden 2 n , por lo que [Dic _n : A ] = 2. Como subgrupo del índice 2, automáticamente es un subgrupo normal . El grupo cociente Dic _n / A es un grupo cíclico de orden 2.

Dic _n es solucionable ; tenga en cuenta que A es normal, y ser abeliano, en sí mismo es solucionable.

Grupo diedro binaria [ editar ]

El grupo dicíclico es un grupo poliédrico binario - es una de las clases de subgrupos del grupo Pin Pin _- (2), que es un subgrupo del grupo Spin Spin (3) - y en este contexto se conoce como el diedro binario grupo .

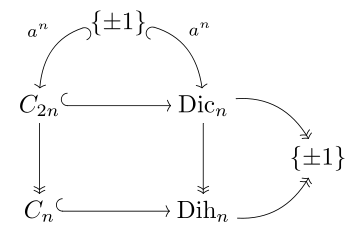
La conexión con el grupo cíclico binario C _2 n , el grupo cíclico C _n y el grupo diédrico Dih _n de orden 2 n se ilustra en el diagrama a la derecha y es paralelo al diagrama correspondiente para el grupo Pin.

Existe una semejanza superficial entre los grupos dicíclicos y los grupos diédricos ; ambos son una especie de "duplicación" de un grupo cíclico subyacente. Pero la presentación de un grupo diedro tendría x ² = 1, en lugar de x ² = a ⁿ ; Y esto produce una estructura diferente. En particular, Dic _n no es un producto semidirectode A y ⟨ x ⟩, ya que A  ∩ ⟨ x ⟩ no es trivial.

El grupo dicíclico tiene una involución única (es decir, un elemento de orden 2), es decir, x ² = a ⁿ . Tenga en cuenta que este elemento se encuentra en el centro de Dic _n . De hecho, el centro consiste únicamente en el elemento de identidad y x ² . Si sumamos la relación x ² = 1 a la presentación de Dic _n, se obtiene una presentación del grupo diédrico Dih _2 n , por lo que el grupo cociente Dic _n / < x ² > es isomorfo de Dih _n .

Existe un homomorfismo natural de 2 a 1 del grupo de cuaterniones unitarios al grupo de rotación tridimensional descrito en los cuaterniones y las rotaciones espaciales . Dado que el grupo dicíclico se puede incrustar dentro de los cuaterniones unitarios, se puede preguntar cuál es la imagen de este bajo homomorfismo. La respuesta es solo el grupo de simetría diédrica Dih _n . Por esta razón, el grupo dicíclico también se conoce como el grupo diedro binario . Tenga en cuenta que el grupo dicíclico no contiene ningún subgrupo isomorfo a Dih _n .

La construcción análoga de pre-imagen, utilizando Pin ₊ (2) en lugar de Pin _- (2), produce otro grupo diedro, Dih _2n , en lugar de un grupo dicíclico.

Generalizaciones [ editar ]

Sea A un grupo abeliano , que tiene un elemento específico y en A con el orden 2. Un grupo G se llama un grupo dicíclico generalizado , escrito como Dic ( A , y ) , si es generado por A y un elemento adicional x , y además, tenemos que [ G : A ] = 2, x ² = y , y para todas a en A , x ⁻¹ ax = a ⁻¹ .

Ya que para un grupo cíclico de orden par, siempre hay un elemento único de orden 2, podemos ver que los grupos dicíclicos son solo un tipo específico de grupo dicíclico generalizado.

grupo de automorfismos de un objeto X es el grupo que consiste en automorfismos de X . Por ejemplo, si X es un espacio vectorial de dimensión finita, entonces el grupo de automorfismo de X es el grupo lineal general de X , el grupo de transformaciones lineales invertibles de X a sí mismo.

Especialmente en contextos geométricos, un grupo de automorfismo también se llama un grupo de simetría . Un subgrupo de un grupo de automorfismo se denomina grupo de transformación (especialmente en la literatura antigua).

Ejemplos [ editar ]

• El grupo de automorfismos de un conjunto X es precisamente el grupo simétrico de X .
• Un homomorfismo de grupo al grupo de automorfismo de un conjunto X equivale a una acción de grupo en X: de hecho, cada acción G izquierda en un conjunto X determina$${\ displaystyle G \ to \ operatorname {Aut} (X), \, g \ mapsto \ sigma _ {g}, \, \ sigma _ {g} (x) = g \ cdot x}Y, a la inversa, cada homomorfismo. $${\ displaystyle \ varphi: G \ to \ operatorname {Aut} (X)} define una acción por $${\ displaystyle g \ cdot x = \ varphi (g) x}.
• Dejar $${\ displaystyle A, B} Serán dos conjuntos finitos de la misma cardinalidad y $${\ displaystyle \ operatorname {Iso} (A, B)} el conjunto de todas las bijections $${\ displaystyle A {\ overset {\ sim} {\ to}} B}. Entonces$${\ displaystyle \ operatorname {Aut} (B)}, que es un grupo simétrico (ver arriba), actúa sobre $${\ displaystyle \ operatorname {Iso} (A, B)}desde la izquierda libre y transitiva; es decir,$${\ displaystyle \ operatorname {Iso} (A, B)}es un torsor para$${\ displaystyle \ operatorname {Aut} (B)}(cf. #En la teoría de la categoría ).
• El grupo automorohismo. $${\ displaystyle G}de un grupo cíclico finito de orden n es isomorfo a$${\ displaystyle (\ mathbb {Z} / n \ mathbb {Z}) ^ {*}} con el isomorfismo dado por $${\ displaystyle {\ overline {a}} \ mapsto \ sigma _ {a} \ en G, \, \ sigma _ {a} (x) = x ^ {a}}. ^[1] En particular,$${\ displaystyle G}Es un grupo abeliano .
• Dada una extensión de campo $${\ displaystyle L / K}, el grupo de automorfismos es el grupo que consiste en automorfismos de campo de L que corrige K : es mejor conocido como el grupo de Galois$${\ displaystyle L / K}.
• El grupo automorphism de la proyectiva n -espacio sobre un campo k es el grupo lineal proyectiva $${\ displaystyle \ operatorname {PGL} _ {n} (k).}^[2]
• El grupo de automorfismo de un álgebra de Lie real de dimensión finita. $${\ displaystyle {\ mathfrak {g}}}tiene la estructura de un grupo de mentiras (real) (de hecho, incluso es un grupo algebraico lineal : ver más abajo). Si G es un grupo de Lie con álgebra de Lie$${\ displaystyle {\ mathfrak {g}}}, entonces el grupo de automorfismo de G tiene una estructura de un grupo de Lie inducida a partir del grupo de automorfismo de G$${\ displaystyle {\ mathfrak {g}}}. ^[3] [4]
• Deje que P sea un finitamente generado módulo proyectivo sobre un anillo R . Luego hay una incrustación.$${\ displaystyle \ operatorname {Aut} (P) \ hookrightarrow \ operatorname {GL} _ {n} (R)}, único hasta automorfismos internos. ^[5]

En la teoría de la categoría [ editar ]

Los grupos de automorfismo parecen muy naturales en la teoría de categorías.

Si X es un objeto en una categoría, entonces el grupo de automorfismo de X es el grupo que consiste en todos los morfismos invertibles de X a sí mismo. Es el grupo de unidades de la monoid endomorphism de X . (Para algún ejemplo, vea PROP .)

Si $${\ displaystyle A, B} son objetos en alguna categoría, entonces el conjunto $${\ displaystyle \ operatorname {Iso} (A, B)} de todo $${\ displaystyle A {\ overset {\ sim} {\ to}} B} es una izquierda $${\ displaystyle \ operatorname {Aut} (B)}-torredor En términos prácticos, esto dice que una elección diferente de un punto base de$${\ displaystyle \ operatorname {Iso} (A, B)}difiere inequívocamente por un elemento de $${\ displaystyle \ operatorname {Aut} (B)}, o que cada elección de un punto base es precisamente una elección de una trivialización del torsor.

Si $${\ displaystyle X_ {i}, i = 1,2} son objetos en categorias $${\ displaystyle C_ {i}} y si $${\ displaystyle F: C_ {1} \ a C_ {2}} es un funtor que mapea $${\ displaystyle X_ {1}} a $${\ displaystyle X_ {2}}, entonces el funtor $${\ displaystyle F} Induce un homomorfismo grupal. $${\ displaystyle \ operatorname {Aut} (X_ {1}) \ to \ operatorname {Aut} (X_ {2})}, como mapea morfismos invertibles a morfismos invertibles.

En particular, si G es un grupo visto como una categoría con un solo objeto * o, más generalmente, si G es un groupoid, entonces cada functor$${\ displaystyle G \ to C}, C una categoría, se llama una acción o una representación de G en el objeto$${\ displaystyle F (*)}, o los objetos $${\ displaystyle F (\ operatorname {Obj} (G))}. Esos objetos entonces se dicen que son$${\ displaystyle G}-objetos (ya que son actuados por $${\ displaystyle G}); cf.$${\ displaystyle \ mathbb {S}}-objeto . Si$${\ displaystyle C} es una categoría de módulo como la categoría de espacios vectoriales de dimensión finita, luego $${\ displaystyle G}-los objetos tambien son llamados $${\ displaystyle G}-módulos.

Grupo de automorfismo functor [ editar ]

Dejar $${\ displaystyle M}ser un espacio vectorial de dimensión finita sobre un campo k equipado con alguna estructura algebraica (es decir, M es un álgebra de dimensión finita sobre k ). Puede ser, por ejemplo, un álgebra asociativao un álgebra de Lie .

Ahora, considere k -mapas lineales$${\ displaystyle M \ to M} que conservan la estructura algebraica: forman un subespacio vectorial. $${\ displaystyle \ operatorname {Fin} _ {\ text {alg}} (M)} de $${\ displaystyle \ operatorname {Fin} (M)}. El grupo de unidades de$${\ displaystyle \ operatorname {Fin} _ {\ text {alg}} (M)} es el grupo de automorfismo $${\ displaystyle \ operatorname {Aut} (M)}. Cuando se elige una base en M ,$${\ displaystyle \ operatorname {Fin} (M)} Es el espacio de matrices cuadradas y $${\ displaystyle \ operatorname {Fin} _ {\ text {alg}} (M)}es el conjunto cero de algunas ecuaciones polinomiales y la invertibilidad se describe nuevamente por los polinomios. Por lo tanto,$${\ displaystyle \ operatorname {Aut} (M)}Es un grupo algebraico lineal sobre k .

Ahora las extensiones de base aplicadas a la discusión anterior determinan un functor: ^{[6] a} saber, para cada anillo conmutativo R sobre k , considere los mapas lineales en R$${\ displaystyle M \ otimes R \ to M \ otimes R} Conservando la estructura algebraica: denotándola por $${\ displaystyle \ operatorname {Fin} _ {\ text {alg}} (M \ otimes R)}. Entonces el grupo de unidades del anillo de la matriz.$${\ displaystyle \ operatorname {Fin} _ {\ text {alg}} (M \ otimes R)}sobre R es el grupo de automorfismo$${\ displaystyle \ operatorname {Aut} (M \ otimes R)} y $${\ displaystyle R \ mapsto \ operatorname {Aut} (M \ otimes R)}es un funtor de grupo : un funtor de la categoría de anillos conmutativos sobre k a la categoría de grupos. Aún mejor, está representado por un esquema (ya que los grupos de automorfismo están definidos por polinomios): este esquema se denomina esquema de grupo de automorfismo y se denota por$${\ displaystyle \ operatorname {Aut} (M)}.

En general, sin embargo, un functor de grupo de automorfismo no puede ser representado por un esquema.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

La flor de Bauhinia blakeana en labandera de la región de Hong Kongtiene simetría C 5 ; La estrella en cada pétalo tiene simetría D 5 .

El símbolo Yin y Yangtiene simetría C 2 de geometría con colores invertidos

En geometría , un grupo de puntos es un grupo de simetrías geométricas ( isometrías ) que mantienen al menos un punto fijo. Los grupos de puntos pueden existir en un espacio euclidiano con cualquier dimensión, y cada grupo de puntos en la dimensión d es un subgrupo del grupo ortogonal O ( d ). Los grupos de puntos se pueden realizar como conjuntos de matrices ortogonales M que transforman el punto x en el punto y :

y = Mx

donde el origen es el punto fijo. Los elementos del grupo de puntos pueden ser rotaciones ( determinante de M = 1) o bien reflexiones , o rotaciones impropias (determinante de M = −1).

Los grupos de puntos discretos en más de una dimensión vienen en familias infinitas, pero a partir del teorema de restricción cristalográfico y uno de los teoremas de Bieberbach , cada número de dimensiones tiene solo un número finito de grupos de puntos que son simétricos en alguna red o cuadrícula con ese número. Estos son los grupos de puntos cristalográficos .

Grupos de puntos quirales y aquirales, grupos de reflexión [ editar ]

Los grupos de puntos se pueden clasificar en grupos quirales (o puramente rotacionales) y grupos aquirales . ^[1]Los grupos quirales son subgrupos del grupo ortogonal especial SO ( d ): contienen solo transformaciones ortogonales que conservan la orientación, es decir, las del determinante +1. Los grupos aquirales contienen también transformaciones del determinante −1. En un grupo aquiral, las transformaciones que preservan la orientación forman un subgrupo (quiral) del índice 2.

Los grupos de Coxeter finitos o grupos de reflexión son aquellos grupos de puntos que se generan puramente por un conjunto de espejos de reflexión que pasan por el mismo punto. Un grupo de Coxeter de rango n tiene nespejos y está representado por un diagrama de Coxeter-Dynkin . La notación de Coxeter ofrece una notación entre corchetes equivalente al diagrama de Coxeter, con símbolos de marcado para la rotación y otros grupos de puntos de subsimetría. Los grupos de reflexión son necesariamente aquirales (excepto el grupo trivial que contiene solo el elemento de identidad).

Lista de grupos de puntos [ editar ]

Una dimensión [ editar ]

Solo hay dos grupos de puntos unidimensionales, el grupo de identidad y el grupo de reflexión.

Grupo	Coxeter	Diagrama de cooxeter	Orden	Descripción
C 1	[] +		1	Identidad
D 1	[]		2	Grupo de reflexión

Dos dimensiones [ editar ]

Grupos de puntos en dos dimensiones , a veces llamados grupos de rosetas .

Vienen en dos familias infinitas:

1. Grupos cíclicos C _n de n grupos de rotación
2. Grupos diédricos D _n de n grupos de rotación y reflexión

La aplicación del teorema de restricción cristalográfica restringe n a los valores 1, 2, 3, 4 y 6 para ambas familias, produciendo 10 grupos.

Grupo	Intl	Orbifold	Coxeter	Orden	Descripción
C n	norte	norte•	[ n ] +	norte	Cíclico: n- rotaciones de plegado. Grupo de resumen Z n , el grupo de enteros bajo módulo de adición n .
D n	n m	*norte•	[norte]	2 n	Catedral: cíclica con reflejos. Resumen del grupo Dih n , el grupo diedro .

Isomorfismo finito y correspondencias.

El subconjunto de grupos de puntos de reflexión puros, definidos por 1 o 2 espejos, también puede ser dado por su grupo de Coxeter y polígonos relacionados. Estos incluyen 5 grupos cristalográficos. La simetría de los grupos de reflexión se puede duplicar mediante un isomorfismo , mapeando ambos espejos entre sí mediante un espejo de bisección, duplicando el orden de simetría.

reflexivo					Rotacional			Polígonos relacionados
Grupo	Grupo de cooxeter		Diagrama de cooxeter		Orden	Subgrupo	Coxeter		Orden
D 1	Un 1	[]			2	C 1	[] +	1	Excavar
D 2	A 1 2	[2]			4	C 2	[2] +	2	Rectángulo
D 3	Un 2	[3]			6	C 3	[3] +	3	Triángulo equilátero
D 4	BC 2	[4]			8	C 4	[4] +	4	Cuadrado
D 5	H 2	[5]			10	C 5	[5] +	5	Pentágono regular
D 6	G 2	[6]			12	C 6	[6] +	6	Hexágono regular
D n	Yo 2(n)	[norte]			2n	C n	[n] +	norte	Polígono regular
D 2 × 2	A 1 2 × 2	[[2]] = [4]		=	8
D 3 × 2	A 2 × 2	[[3]] = [6]		=	12
D 4 × 2	BC 2 × 2	[[4]] = [8]		=	dieciséis
D 5 × 2	H 2 × 2	[[5]] = [10]		=	20
D 6 × 2	G 2 × 2	[[6]] = [12]		=	24
D n × 2	I 2 (n) × 2	[[n]] = [2n]		=	4 n

Tres dimensiones [ editar ]

Artículo principal: Grupos de puntos en tres dimensiones.

Grupos de puntos en tres dimensiones , a veces llamados grupos de puntos moleculares después de su amplio uso en el estudio de las simetrías de moléculas pequeñas .

Vienen en 7 familias infinitas de grupos axiales o prismáticos, y 7 grupos poliédricos o platónicos adicionales. En notación de Schönflies , *

• Grupos axiales: C _n , S _2n , C _n h , C _n v , D _n , D _n d , D _n h
• Grupos poliédricos : T, T _d , T _h , O, O _h , I, I _h

La aplicación del teorema de restricción cristalográfica a estos grupos da como resultado 32 grupos de puntos cristalográficos .

Dominios fundamentales de los grupos reflexivos de color par / impar.

C 1v Orden 2	C 2v Orden 4	C 3v Orden 6	C 4v Orden 8	C 5v Orden 10	C 6v Orden 12	...
D 1h Orden 4	D 2h Orden 8	D 3h Orden 12	D 4h Orden 16	D 5h Orden 20	D 6h Orden 24	...
T d orden 24	O h orden 48	Yo h pedido 120

Intl * Geo [2] Orbifold Schönflies Conway Coxeter Orden 1 1 1 C 1 C 1 [] + 1 1 22 × 1 C i = S 2 Cc 2 [2 + , 2 +] 2 2 = m 1 * 1 C s = C 1v= C 1h ± C 1 = CD 2 [] 2 2  3  4  5  6  n 2  3  4  5  6  n 22  33  44  55  66  nn C 2 C 3 C 4 C 5 C 6 C n C 2 C 3 C 4 C 5 C 6 C n [2] + [3] + [4] + [5] + [6] + [n] + 2  3  4  5  6  n mm2 3m  4mm 5m  6mm nmm nm 2  3  4  5  6  n * 22  * 33  * 44  * 55  * 66  * nn C 2v C 3v C 4v C 5v C 6v C nv CD 4 CD 6 CD 8 CD 10 CD 12 CD 2n [2]  [3]  [4]  [5]  [6]  [n] 4  6  8  10  12  2n 2 / m 6 4 / m 10 6 / m n / m 2n 2 2  3 2  4 2  5 2  6 2  n 2 2 *  3 *  4 *  5 *  6 *  n * C 2h C 3h C 4h C 5h C 6h C nh ± C 2 CC 6 ± C 4 CC 10 ± C 6 ± C n / CC 2n [2,2 + ]  [2,3 + ]  [2,4 + ]  [2,5 + ]  [2,6 + ]  [2, n + ] 4  6  8  10  12  2n 4  3  8  5  12  2n  n 4 2  6 2  8 2  10 2  12 2  2n 2 2 ×  3 ×  4 ×  5 ×  6 ×  n × S 4 S 6 S 8 S 10 S 12 S 2n CC 4 ± C 3 CC 8 ± C 5 CC 12 CC 2n / ± C n [2 + , 4 +]  [2 + , 6 +]  [2 + , 8 +]  [2 + , 10+ ]  [2 + , 12+ ]  [2 + , 2n+ ] 4  6  8  10  12  2n

Intl Geo Orbifold Schönflies Conway Coxeter Orden 222  32  422  52  622  n22  n2 2 2  3 2  4 2  5 2  6 2  n 2 222  223  224  225  226  22n D 2 D 3 D 4 D 5 D 6 D n D 4 D 6 D 8 D 10 D 12 D 2n [2,2] + [2,3] + [2,4] + [2,5] + [2,6] + [2, n] + 4  6  8  10  12  2 n mmm 6 m2  4 / mmm 10m2  6 / mmm n / mmm 2nm2 2 2  3 2  4 2  5 2  6 2  n 2 * 222  * 223  * 224  * 225  * 226  * 22n D 2h D 3h D 4h D 5h D 6h D nh ± D 4 DD 12 ± D 8 DD 20 ± D 12 ± D 2n / DD 4n [2,2]  [2,3]  [2,4]  [2,5]  [2,6]  [2, n] 8  12  16  20  24  4n 4 2m  3 m  8 2m  5 m  122m  2n2m  n m 4 2 6 2 8 2 10 2 12 2 n 2 2 * 2  2 * 3  2 * 4  2 * 5  2 * 6  2 * n D 2d D 3d D 4d D 5d D 6d D nd ± D 4 ± D 6 DD 16 ± D 10 DD 24 DD 4n / ± D 2n [2 + , 4]  [2 + , 6]  [2 + , 8]  [2 + , 10]  [2 + , 12]  [2 + , 2n] 8  12  16  20  24  4n 23 3 3 332 T T [3,3] + 12 m 3 4 3 3 * 2 T h ± T [3 + , 4] 24 4 3m 3 3 * 332 T d A [3,3] 24 432 4 3 432 O O [3,4] + 24 m 3m 4 3 * 432 O h ± O [3,4] 48 532 5 3 532 yo yo [3,5] + 60 5 3 m 5 3 * 532 Yo h ± yo [3,5] 120

(*) Cuando las entradas de Intl están duplicadas, la primera es para n , la segunda para n impar .