cuatro grupos de Klein es un grupo con cuatro elementos, en el que cada elemento es autoinverso (al componerlo produce la identidad) y al componer dos de los tres elementos que no son de identidad produce el tercero. Puede describirse como el grupode simetría de un rectángulo no cuadrado (con los tres elementos de no identidad como reflexión horizontal y vertical y rotación de 180 grados), como el grupo de bit a bit exclusivo o operaciones en valores binarios de dos bits, o Más abstracto como Z 2 × Z 2 , el producto directo.de dos copias del grupo cíclico de orden 2. Fue nombrado Vierergruppe (que significa cuatro grupos) por Felix Klein en 1884. [1]También se llama el grupo Klein , y a menudo está simbolizado por la letra V o como K 4 .
El cuatro grupos de Klein, con cuatro elementos, es el grupo más pequeño que no es un grupo cíclico . Solo hay otro grupo de orden cuatro, hasta el isomorfismo , el grupo cíclico de orden 4. Ambos son grupos abelianos . El grupo más pequeño no abeliano es el grupo simétrico de grado 3 , que tiene orden 6.
Presentaciones [ editar ]
| * | mi | una | segundo | do |
|---|---|---|---|---|
| mi | mi | una | segundo | do |
| una | una | mi | do | segundo |
| segundo | segundo | do | mi | una |
| do | do | segundo | una | mi |
El grupo de cuatro Klein también se define por la presentación del grupo.
Todos los elementos de no identidad del grupo Klein tienen orden 2, por lo tanto, cualquiera de los dos elementos de no identidad puede servir como generadores en la presentación anterior. El cuatro grupos de Klein es el grupo no cíclico más pequeño . Sin embargo, es un grupo abeliano , e isomorfo al grupo diédrico de orden (cardinalidad) 4, es decir, D 4 (o D 2 , usando la convención geométrica); Aparte del grupo de orden 2, es el único grupo diedro que es abeliano.
El cuatro grupos de Klein también es isomorfo a la suma directa Z 2 ⊕ Z 2 , de modo que puede representarse como los pares {(0,0), (0,1), (1,0), (1,1 )} bajo el módulo de adición por componentes 2 (o, de manera equivalente, las cadenas de bits {00, 01, 10, 11} bajo XOR a nivel de bits ); siendo (0,0) el elemento de identidad del grupo. El cuatro grupos de Klein es, por lo tanto, un ejemplo de un grupo 2 abeliano elemental , que también se conoce como grupo booleano . El cuatro grupos de Klein es también el grupo generado por la diferencia simétrica como la operación binaria en los subconjuntos de unconjunto de potencias de un conjunto con dos elementos, es decir, sobre un campo de conjuntos con cuatro elementos, por ejemplo; el conjunto vacío es el elemento de identidad del grupo en este caso.
Otra construcción numérica de los cuatro grupos de Klein es el conjunto {1, 3, 5, 7}, siendo la operación el módulo de multiplicación 8 . Aquí a es 3, b es 5, y c = ab es 3 × 5 = 15 ≡ 7 (mod 8) .
Geometría [ editar ]
Geométricamente, en dos dimensiones, el cuatro grupos de Klein es el grupo de simetría de un rombo y de rectángulos que no son cuadrados , los cuatro elementos son la identidad, la reflexión vertical, la reflexión horizontal y una rotación de 180 grados.
En tres dimensiones hay tres grupos de simetría diferentes que son algebraicamente los cuatro grupos V de Klein:
- Uno con tres ejes de rotación perpendiculares de 2 pliegues: D 2
- uno con un eje de rotación de 2 veces y un plano de reflexión perpendicular: C 2 h = D 1 d
- uno con un eje de rotación de 2 veces en un plano de reflexión (y, por lo tanto, también en un plano de reflexión perpendicular): C 2 v = D 1 h .
Representación de permutación [ editar ]
Los tres elementos del orden dos en el cuatro grupos de Klein son intercambiables: el grupo de automorfismo de V es el grupo de permutaciones de estos tres elementos.
Las permutaciones de los cuatro grupos de Klein de sus propios elementos se pueden considerar de manera abstracta como su representación de permutación en cuatro puntos:
- V = {(), (1,2) (3,4), (1,3) (2,4), (1,4) (2,3)}
En esta representación, V es un subgrupo normal del grupo alterno A 4 (y también el grupo simétrico S 4 ) en cuatro letras. De hecho, es el núcleode un homomorfismo de grupo superyectivo de S 4 a S 3 .
Otras representaciones dentro de S 4 son:
{(), (1,2), (3,4), (1,2) (3,4)}
{(), (1,3), (2,4), (1,3) (2,4)}
{(), (1,4), (2,3), (1,4) (2,3)}
No son subgrupos normales de S 4.
Álgebra [ editar ]
Según la teoría de Galois , la existencia de los cuatro grupos de Klein (y, en particular, la representación de la permutación de la misma) explica la existencia de la fórmula para calcular las raíces de las ecuaciones quárticasen términos de radicales , según lo establecido por Lodovico Ferrari : el mapa S 4 → S 3 corresponde a la resolución cúbica, en términos de resolución de Lagrange .
En la construcción de anillos finitos , ocho de los once anillos con cuatro elementos tienen el grupo de cuatro Klein como su subestructura aditiva.
Si R × denota el grupo multiplicativo de reales no cero y R + el grupo multiplicativo de reales positivos , R × × R ×es el grupo de unidades del anillo R × R , y R + × R + es un subgrupo de R × × R × (de hecho es el componente de la identidad de R × × R × ). El grupo cociente ( R ×× R × ) / ( R + × R + ) es isomorfo para los cuatro grupos de Klein. De manera similar, el grupo de unidades del anillo de números de complejo dividido, cuando se divide por su componente de identidad, también da como resultado el cuatro grupos de Klein.
La teoría de grafos [ editar ]
El gráfico conectado más simple y simple que admite el grupo de cuatro Klein como su grupo de automorfismo es el gráfico de diamante que se muestra a continuación. También es el grupo de automorfismo de algunos otros gráficos que son más simples en el sentido de tener menos entidades. Estos incluyen el gráfico con cuatro vértices y un borde, que sigue siendo simple pero pierde la conectividad, y el gráfico con dos vértices conectados entre sí por dos bordes, que permanece conectado pero pierde la simplicidad.
Musica [ editar ]
En la composición musical, el grupo de cuatro es el grupo básico de permutaciones en la técnica de doce tonos . En ese caso se escribe la tabla de Cayley; [2]
| S | YO: | R: | RHODE ISLAND: |
| YO: | S | Rhode Island | R |
| R: | Rhode Island | S | yo |
| RHODE ISLAND: | R | yo | S |
grupo de cuaternión Q 8 (a veces solo denotado por Q) es un grupo no abeliano de orden ocho, isomorfo a un cierto subconjunto de ocho elementos de los cuaterniones bajo multiplicación. Está dada por la presentación grupal.
Comparado con el grupo diedro [ editar ]
El grupo de cuaternión Q 8 tiene el mismo orden que el grupo diedro D 4 , pero una estructura diferente, como lo muestran sus gráficos de Cayley y de ciclo:
| Q 8 | D 4 | |
|---|---|---|
| Gráfica de Cayley | 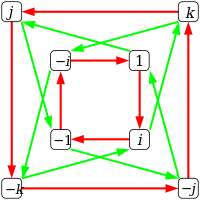 Las flechas rojas representan la multiplicación por i , las flechas verdes por j . |  |
| Gráfico de ciclo | 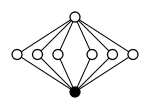 |  |
El grupo diedro D 4 se puede realizar como un subconjunto de los split cuaterniones en la misma manera que Q 8se puede ver como un subconjunto de los cuaterniones.
Mesa de Cayley [ editar ]
| × | mi | mi | yo | yo | j | j | k | k |
|---|---|---|---|---|---|---|---|---|
| mi | mi | mi | yo | yo | j | j | k | k |
| mi | mi | mi | yo | yo | j | j | k | k |
| yo | yo | yo | mi | mi | k | k | j | j |
| yo | yo | yo | mi | mi | k | k | j | j |
| j | j | j | k | k | mi | mi | yo | yo |
| j | j | j | k | k | mi | mi | yo | yo |
| k | k | k | j | j | yo | yo | mi | mi |
| k | k | k | j | j | yo | yo | mi | mi |
Propiedades [ editar ]
El grupo de cuaternión tiene la propiedad inusual de ser hamiltoniano : cada subgrupo de Q 8 es un subgrupo normal , pero el grupo no es abeliano. [2] Cada grupo hamiltoniano contiene una copia de Q 8 . [3]
El grupo cuaternión Q 8 es uno de los dos ejemplos más pequeños de un grupo no abeliano nilpotent, siendo el otro el grupo diedro D 4 de orden 8.
El grupo de cuaternión Q 8 tiene cinco representaciones irreductibles, y sus dimensiones son 1,1,1,1,2. La prueba de esta propiedad no es difícil, ya que el número de caracteres irreductibles de Q 8 es igual al número de sus clases de conjugación, que es cinco ({e}, { e }, {i, i }, {j, j }, {k, k }).
Estas cinco representaciones son las siguientes:
Representación trivial
Las representaciones de signos con i, j, k-kernel : Q 8 tienen tres subgrupos normales máximos: los subgrupos cíclicos generados por i, j y k, respectivamente. Para cada subgrupo normal máximo, obtenemos una representación unidimensional con ese subgrupo como núcleo. La representación envía elementos dentro del subgrupo a 1, y elementos fuera del subgrupo a -1.
Representación bidimensional : una representación: Se da a continuación en la sección de representaciones de Matrix.
Entonces, la tabla de caracteres del grupo de cuaternión Q 8 , que resulta ser la misma que la tabla de caracteres del grupo diédrico D 4 , es:
| Clase de representación / conjugación | {e} | { e } | {i, i } | {j, j } | {k, k } |
|---|---|---|---|---|---|
| Representación trivial | 1 | 1 | 1 | 1 | 1 |
| Firmar representaciones con i-kernel | 1 | 1 | 1 | -1 | -1 |
| Signos de representaciones con j-kernel. | 1 | 1 | -1 | 1 | -1 |
| Signos de representaciones con k-kernel. | 1 | 1 | -1 | -1 | 1 |
| Representación bidimensional | 2 | -2 | 0 | 0 | 0 |
En álgebra abstracta , se puede construir un espacio vectorial de cuatro dimensiones real como el cociente del anillo de grupo R [Q] por el ideal definido por el tramo R ({e + e , i + i , j + j , k + k }) . [ citación necesitada ] El resultado es un campo sesgado llamado los cuaterniones . Tenga en cuenta que esto no es exactamente lo mismo que el álgebra de grupo en Q 8 (que sería de ocho dimensiones). Por el contrario, uno puede comenzar con los cuaterniones ydefine el grupo de cuaternión como el subgrupo multiplicativo que consiste en los ocho elementos {1, −1, i , - i , j , - j , k , - k }. El complejo espacio vectorial de cuatro dimensiones, sobre la misma base, se denomina álgebra de biquaterniones .
Tenga en cuenta que i, j y k tienen orden cuatro en Q 8 y cualquiera de ellos genera el grupo completo. Otra presentación de Q 8 [4] que demuestra esto es:
Uno puede tomar, por ejemplo, i = x, j = y y k = xy.
El centro y el subgrupo de conmutadores de Q 8 es el subgrupo {e, e }. El grupo de factores Q 8 / {e, e } es isomorfo para los cuatro grupos Klein V. El grupo de automorfismos internos de Q 8 es isomorphic para Q 8 en su centro, y por lo tanto también es isomorphic para los cuatro grupos de Klein. El grupo de automorfismo completo de Q 8 es isomorfo al grupo simétrico de grado 4, S 4 , elGrupo simétrico en cuatro letras. El grupo de automorfismo externo de Q 8 es entonces S 4 / V, que es isomorfo a S 3 .
Representaciones matriciales [ editar ]
El grupo de cuaternión se puede representar como un subgrupo del grupo lineal general GL 2 ( C ). Una representación
es dado por
Dado que todas las matrices anteriores tienen unidad determinante, esta es una representación de Q 8 en el grupo lineal especial SL 2 ( C ). Las identidades estándar para la multiplicación de cuaterniones se pueden verificar utilizando las leyes habituales de la multiplicación de matrices en GL 2 ( C ). [5]
También hay una acción importante de Q 8 en los ocho elementos distintos de cero del espacio vectorial bidimensional sobre el campo finito F 3 . Una representación
es dado por
donde {−1, 0, 1} son los tres elementos de F 3 . Como todas las matrices anteriores tienen una unidad determinante sobre F 3 , esta es una representación de Q 8 en el grupo lineal especial SL (2, 3) . De hecho, el grupo SL (2, 3) tiene orden 24, y Q 8 es un subgrupo normal de SL (2, 3) del índice 3.
Grupo de Galois [ editar ]
Como Richard Dean mostró en 1981, el grupo cuaternión se puede presentar como el grupo Galois Gal ( T / Q) donde Q es el campo de los números racionales y T es el campo de división , sobre Q, del polinomio
- .
El desarrollo utiliza el teorema fundamental de la teoría de Galois al especificar cuatro campos intermedios entre Q y T y sus grupos de Galois, así como dos teoremas sobre la extensión cíclica del grado cuatro sobre un campo. [6]
Grupo de cuaterniones generalizada [ editar ]
Es una parte de la clase más general de grupos dicíclicos.
Algunos autores definen que [4] grupo de cuaternión generalizado es el mismo que el grupo dicíclico .
para algún entero n ≥ 2 . Este grupo se denota Q 4 n y tiene orden 4 n . [8] Coxeter etiqueta estos grupos dicíclicos <2 font="" nbsp="">n >, siendo un caso especial del grupo poliédrico binario < l , m , n > y están relacionados con los grupos poliédricos ( p , q , r ) y el grupo diédrico ( 2,2, n ). El grupo de cuaternión habitual corresponde al caso n = 2.. El grupo de cuaternión generalizado se puede realizar como el subgrupo de GL 2 ( C ) generado por
donde ω n = e iπ / n . [4] También se puede realizar como el subgrupo de cuaterniones unitarios generado por [9]x = e iπ / n y y = j .
Los grupos de cuaternión generalizados tienen la propiedad de que cada subgrupo abeliano es cíclico. [10] Se puede demostrar que un finito p -Grupo con esta propiedad (cada subgrupo abeliano es cíclico) es o cíclico o un grupo cuaternión generalizada como se definió anteriormente. [11] Otra caracterización es que un grupo p finito en el que hay un subgrupo único de orden p es cíclico o un grupo de cuaterniones generalizados de 2 grupos isomorfos a cuaternarios. [12] En particular, para un campo finito F con característica impar, el subgrupo 2-Sylow de SL 2 ( F) no es abeliano y solo tiene un subgrupo de orden 2, por lo que este subgrupo 2-Sylow debe ser un grupo de cuaternión generalizado ( Gorenstein 1980 , p. 42). Si p r tiene el tamaño de F , donde p es primo, el tamaño del subgrupo 2-Sylow de SL 2 ( F ) es 2 n , donde n = ord 2 ( p 2 - 1) + ord 2 ( r ) .
El teorema de Brauer-Suzuki muestra que los grupos cuyos 2 subgrupos de Sylow son cuaterniones generalizados no pueden ser simples.




















No hay comentarios:
Publicar un comentario