LISTA DE TEMAS MATEMÁTICOS - ÁLGEBRA ABSTRACTA

grupo de Dedekind es un grupo G tal que cada subgrupo de G es normal . Todos los grupos abelianos son grupos de Dedekind. Un grupo de Dedekind no abeliano se llama grupo hamiltoniano . ^[1]

El ejemplo más familiar (y más pequeño) de un grupo hamiltoniano es el grupo de cuaternión de orden 8, denotado por Q ₈ . Dedekind y Baer han demostrado (en el caso de orden finito y orden infinito respectivamente) que cada grupo hamiltoniano es un producto directo de la forma G = Q ₈ × B × D , donde B es un grupo abeliano elemental de 2 , y D es un periódico Grupo abeliano con todos los elementos de orden impar.

Los grupos de Dedekind llevan el nombre de Richard Dedekind , quien los investigó en ( Dedekind 1897 ), lo que demuestra una forma del teorema de estructura anterior (para grupos finitos ). Nombró a los no abelianos como William Rowan Hamilton , el descubridor de los cuaterniones .

En 1898, George Miller delineó la estructura de un grupo hamiltoniano en términos de su orden y la de sus subgrupos. Por ejemplo, se muestra "un grupo Hamilton de orden 2 ^una tiene 2 ^{2 un - 6} cuaternión grupos como subgrupos". En 2005, Horvat et al ^[2] utilizaron esta estructura para contar el número de grupos hamiltonianos de cualquier orden n = 2 ^e o donde o es un número entero impar. Cuando e <3 font=""> entonces no hay grupos hamiltonianos de orden n , de lo contrario hay el mismo número que hay grupos abelianos de orden o.

ejemplos elementales de grupos en matemáticas se dan en Grupo (matemáticas) . Más ejemplos se enumeran aquí.

Permutaciones de un conjunto de tres elementos [ editar ]

Gráfico de ciclos para S ₃ . Un bucle especifica una serie de potencias de cualquier elemento conectado al elemento de identidad (e). Por ejemplo, el bucle e-ba-ab refleja el hecho de que ba ² = ab y ba ³ = e, así como el hecho de que ab ² = ba y ab ³= e Los otros "bucles" son raíces de la unidad, de modo que, por ejemplo, ² = e.

Artículo principal: Grupo diedro de orden 6.

Considere tres bloques de colores (rojo, verde y azul), inicialmente colocados en el orden RGB. Sea a la operación "intercambiar el primer bloque y el segundo bloque", y b ser la operación "intercambiar el segundo bloque y el tercer bloque".

Podemos escribir xy para la operación "primero hacer y , luego hacer x "; de modo que ab es la operación RGB → RBG → BRG, que podría describirse como "mover los dos primeros bloques una posición a la derecha y colocar el tercer bloque en la primera posición". Si escribimos e para "dejar los bloques como están" (la operación de identidad), entonces podemos escribir las seis permutaciones de los tres bloques de la siguiente manera:

• e  : RGB → RGB
• a  : RGB → GRB
• b  : RGB → RBG
• ab  : RGB → BRG
• ba  : RGB → GBR
• aba  : RGB → BGR

Tenga en cuenta que aa tiene el efecto RGB → GRB → RGB; para que podamos escribir aa = e . De manera similar, bb = ( aba ) ( aba ) = e ; ( ab ) ( ba ) = ( ba ) ( ab ) = e ; entonces cada elemento tiene un inverso.

Por inspección, podemos determinar la asociatividad y el cierre; note en particular que ( ba ) b = aba = b ( ab ).

Como se construye a partir de las operaciones básicas a y b , decimos que el conjunto { a , b } genera este grupo. El grupo, llamado grupo simétrico S ₃ , tiene orden 6 y no es abeliano (ya que, por ejemplo, ab ≠ ba ).

El grupo de traducciones del plano [ editar ]

Una traslación del plano es un movimiento rígido de cada punto del plano por una cierta distancia en cierta dirección. Por ejemplo, "moverse en dirección noreste 2 millas" es una traducción del avión. Si tiene dos de esas traducciones a y b , se pueden componer para formar una nueva traducción a ∘ b de la siguiente manera: primero siga la prescripción de b , luego la de a . Por ejemplo, si

a = "mover al noreste por 3 millas"

y

b = "mover al sureste por 4 millas"

entonces

a ∘ b = "mover hacia el este por 5 millas"

(vea el teorema de Pitágoras para saber por qué esto es así, geométricamente).

El conjunto de todas las traducciones del plano con composición como operación forma un grupo:

1. Si un y b son traducciones, a continuación, un ∘ b es también una traducción.
2. La composición de las traducciones es asociativa: ( a ∘ b ) ∘ c = a ∘ ( b ∘ c ).
3. El elemento de identidad para este grupo es la traducción con receta "mueva cero millas en la dirección que desee".
4. Lo inverso de una traducción se da caminando en la dirección opuesta por la misma distancia.

Este es un grupo abeliano y nuestro primer ejemplo (no discreto) de un grupo de Lie : un grupo que también es múltiple .

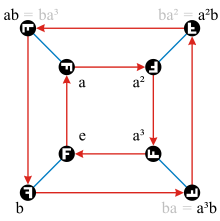
El grupo de simetría de un cuadrado: grupo diedro de orden 8.[ editar ]

El gráfico del ciclo de Dih ₄ 
a es la rotación en el sentido de las agujas del reloj 
y b la reflexión horizontal.

Dih 4 como grupo de puntos 2D, D 4 , [4], (* 4 •), orden 4, con una rotación de 4 veces y un generador de espejo.

Dih 4 en 3D grupo diédrico D4 , [4,2] + , (422), orden 4, con un generador de rotación vertical de 4 pliegues orden 4 y generador de 2 veces horizontal

Cayley gráfica de Dih ₄

Un gráfico de Cayley diferente de Dih ₄ , generado por la reflexión horizontal b y una reflexión diagonal c

Los grupos son muy importantes para describir la simetría de los objetos, ya sean geométricos (como un tetraedro ) o algebraicos (como un conjunto de ecuaciones). Como ejemplo, consideramos un cuadrado de vidrio de un cierto grosor (con una letra "F" escrita en él, solo para hacer que las diferentes posiciones sean discriminables). Para describir su simetría, formamos el conjunto de todos esos movimientos rígidos del cuadrado que no hacen una diferencia visible (excepto la "F"). Por ejemplo, si lo giras 90 ° en el sentido de las agujas del reloj, sigue pareciendo igual, por lo que este movimiento es un elemento de nuestro conjunto, llamémoslo un. También podríamos voltearlo horizontalmente para que su parte inferior quede hacia arriba. Nuevamente, después de realizar este movimiento, el cuadrado de vidrio tiene el mismo aspecto, por lo que este es también un elemento de nuestro conjunto y lo llamamos b . Luego está, por supuesto, el movimiento que no hace nada; se denota por e .

Ahora, si tiene dos de esos movimientos x e y , puede definir la composición x ∘ y como se indica arriba: primero realice el movimiento y,luego, el movimiento x . El resultado dejará la losa como antes.

El punto es que el conjunto de todos esos movimientos, con la composición como operación, forma un grupo. Este grupo es la descripción más concisa de la simetría del cuadrado. Los químicos usan grupos de simetría de este tipo para describir la simetría de cristales y moléculas.

Investiguemos un poco más nuestro grupo de simetría de cuadrados. En este momento, tenemos los elementos un , b y e , pero podemos formar fácilmente más: por ejemplo un ∘ una , también escrito como un ² , es un giro de 180 ° grados. a ³ es una rotación de 270 ° en el sentido de las agujas del reloj (o una rotación de 90 ° en el sentido de las agujas del reloj). También vemos que b ² = e , y también una ⁴ = e . Aquí hay una interesante: ¿qué hace un ∘ b ? Primero voltea horizontalmente, luego gira. Intenta visualizar que a ∘ b= b ∘ a ³ . Además, a ²∘ b es un giro vertical y es igual a b ∘ a ² .

Este grupo de orden 8 tiene la siguiente tabla de Cayley :

o	mi	segundo	una	un 2	un 3	ab	a 2 b	a 3 b
mi	mi	segundo	una	un 2	un 3	ab	a 2 b	a 3 b
segundo	segundo	mi	a 3 b	a 2 b	ab	un 3	un 2	una
una	una	ab	un 2	un 3	mi	a 2 b	a 3 b	segundo
un 2	un 2	a 2 b	un 3	mi	una	a 3 b	segundo	ab
un 3	un 3	a 3 b	mi	una	un 2	segundo	ab	a 2 b
ab	ab	una	segundo	a 3 b	a 2 b	mi	un 3	un 2
a 2 b	a 2 b	un 2	ab	segundo	a 3 b	una	mi	un 3
a 3 b	a 3 b	un 3	a 2 b	ab	segundo	un 2	una	mi

Para cualquiera de los dos elementos en el grupo, la tabla registra cuál es su composición.

Aquí escribimos " a ³ b " como una taquigrafía para un ³ ∘ b .

En matemáticas, este grupo se conoce como grupo diédrico de orden 8 y se denomina Dih ₄ , D ₄ o D ₈ , según la convención. Este fue un ejemplo de un grupo no abeliano: la operación ∘ aquí no es conmutativa , como se puede ver en la tabla; La tabla no es simétrica respecto a la diagonal principal.

El grupo diedro de orden 8 es isomorfo al grupo de permutación generado por (1234) y (13) .

Grupo libre en dos generadores [ editar ]

El grupo libre con dos generadores a y b consta de todas las cadenas finitas que pueden formarse a partir de los cuatro símbolos a , a ⁻¹ , b y b ^{−1, de} modo que no a aparece directamente junto a a ⁻¹ y no b aparece directamente al lado de un b ⁻¹ . Dos cadenas de este tipo se pueden concatenar y convertir en una cadena de este tipo reemplazando repetidamente las subcadenas "prohibidas" por la cadena vacía. Por ejemplo: " abab ⁻¹ a ⁻¹ " concatenado con "abab ⁻¹ a "cede" abab ⁻¹ a ⁻¹ abab ⁻¹ a ", que se reduce a" abaab ⁻¹ a ". Se puede verificar que el conjunto de esas cadenas con esta operación forme un grupo con un elemento neutral el vacío string ε: = "". (Por lo general, las comillas no aparecen, por lo que necesita el símbolo ε!)

Este es otro grupo infinito no abeliano.

Los grupos libres son importantes en la topología algebraica ; El grupo libre en dos generadores también se usa para probar la paradoja de Banach-Tarski .

El conjunto de mapas [ editar ]

Los conjuntos de mapas de un conjunto a un grupo [ editar ]

Sea G un grupo y S un conjunto no vacío. El conjunto de mapas M ( S ,  G ) es en sí mismo un grupo; a saber, para dos mapas f, g de S en G , definimos fg como el mapa tal que ( fg ) ( x ) =  f ( x ) g ( x ) para cada x ∈ S y f ⁻¹sea ​​el mapa tal que f ⁻¹ ( x ) =  f ( x ) ⁻¹.

Tome los mapas f , g y h en M (S, G) . Para cada x en S , f ( x ) y g ( x ) están en G , y también lo es ( fg ) ( x ). Por lo tanto, fg también está en M ( S ,  G ), o M ( S ,  G ) está cerrado. Para (( fg ) h ) ( x ) = ( fg ) ( x ) h( x ) = ( f ( x ) g ( x )) h ( x ) =  f ( x ) ( g ( x ) h ( x )) =  f ( x ) ( gh ) ( x ) = ( f ( gh ) ) ( x ), M ( S ,  G ) es asociativa. Y hay un mapa i tal que i ( x ) =  e dondee es el elemento unidad de G . El mapa i hace todas las funciones f en M ( S ,  G ) de modo que si  =  fi  =  f , o i es el elemento unitario de M ( S ,  G ). Por lo tanto, M ( S ,  G ) es en realidad un grupo.

Si G es conmutativo, entonces ( fg ) ( x ) =  f ( x ) g ( x ) =  g ( x ) f ( x ) = ( gf ) ( x ). Por lo tanto, también lo es M ( S ,  G ).

Grupos de automorfismo [ editar ]

Grupos de permutaciones [ editar ]

Sea G el conjunto de asignaciones biyectivas de un conjunto S sobre sí mismo. Entonces G forma un grupo bajo la composición ordinaria de mapeos. Este grupo se llama el grupo simétrico , y comúnmente se denota denotado como Sym (S) , Σ _S , o$${\ displaystyle {\ mathfrak {S}} _ {S}}. El elemento de unidad de G es el mapa de identidad de S . Para dos mapas f y g en G son biyectivos, fg también es biyectivo. Por lo tanto, G está cerrado. La composición de los mapas es asociativa; por lo tanto, G es un grupo. S puede ser finito o infinito.

Grupos de matrices [ editar ]

Si n es algún entero positivo, podemos considerar el conjunto de todas las matrices invertibles n por n sobre los reales , por ejemplo. Este es un grupo con la multiplicación de matrices como operación. Se llama el grupo lineal general , GL ( n ). Geométricamente, contiene todas las combinaciones de rotaciones, reflexiones, dilataciones y transformaciones de inclinación del espacio euclidiano n- dimensional que fijan un punto determinado (el origen ).

Si nos limitamos a matrices con el determinante 1, obtenemos otro grupo, el grupo lineal especial , SL ( n ). Geométricamente, esto consiste en todos los elementos de GL ( n ) que conservan la orientación y el volumen de los diversos sólidos geométricos en el espacio euclidiano.

Si, por el contrario, nos limitamos a matrices ortogonales , obtenemos el grupo ortogonal O ( n ). Geométricamente, esto consiste en todas las combinaciones de rotaciones y reflexiones que fijan el origen. Estas son precisamente las transformaciones que conservan longitudes y ángulos.

Finalmente, si imponemos ambas restricciones, obtenemos el grupo ortogonal especial SO ( n ), que consiste solo en rotaciones.

Estos grupos son nuestros primeros ejemplos de grupos infinitos no abelianos. También son grupos de mentiras . De hecho, la mayoría de los grupos de Lie importantes (pero no todos) se pueden expresar como grupos de matriz.

Si esta idea se generaliza a matrices con números complejos como entradas, obtendremos otros grupos de Lie útiles, como el grupo unitario U ( n ). También podemos considerar matrices con cuaterniones como entradas; en este caso, no hay una noción bien definida de un determinante (y, por lo tanto, no hay una buena manera de definir un "volumen" cuaterniónico), pero aún podemos definir un grupo análogo al grupo ortogonal, el grupo simpléctico Sp ( n ).

Además, la idea puede tratarse de forma puramente algebraica con matrices sobre cualquier campo , pero luego los grupos no son grupos de Lie.

Por ejemplo, tenemos los grupos lineales generales sobre campos finitos . El teórico del grupo JL Alperin ha escrito que "el ejemplo típico de un grupo finito es GL (n, q), el grupo lineal general de n dimensiones sobre el campo con elementos q. El estudiante que es introducido al tema con otros ejemplos es siendo completamente engañado ". 

grupo de permutación es un grupo G cuyos elementos son permutaciones de un conjunto M dado y cuya operación de grupo es la composición de las permutaciones en G (que se consideran funciones biyectivas del conjunto M a sí mismo). El grupo de todas las permutaciones de un conjunto M es el grupo simétrico de M , a menudo escrito como Sym ( M ). ^[1] El término grupo de permutación significa un subgrupodel grupo simétrico. Si M = {1,2, ..., n } entonces, Sym ( M ), el grupo simétrico en n letrasgeneralmente se denota por S _n .

Según el teorema de Cayley , cada grupo es isomorfo a algún grupo de permutación.

La forma en que los elementos de un grupo de permutación permutan los elementos del conjunto se denomina acción de grupo . Las acciones grupales tienen aplicaciones en el estudio de simetrías , combinatoria y muchas otras ramas de las matemáticas , la física y la química.

El popular rompecabezas del cubo de Rubik, inventado en 1974 por Ernő Rubik, se ha utilizado como ilustración de los grupos de permutación. Cada rotación de una capa del cubo da como resultado una permutación de los colores de la superficie y es un miembro del grupo. El grupo de permutación del cubo se llama el grupo de cubos de Rubik .

Propiedades básicas y terminología [ editar ]

Al ser un subgrupo de un grupo simétrico, todo lo que es necesario para que un conjunto de permutaciones satisfaga los axiomas de grupo y sea un grupo de permutación es que contiene la permutación de la identidad, la permutación inversa de cada permutación que contiene, y se cierra bajo la composición de Sus permutaciones. ^[2] Una propiedad general de los grupos finitos implica que un subconjunto no vacío finito de un grupo simétrico es nuevamente un grupo si y solo si está cerrado bajo la operación de grupo. ^[3]

El grado de un grupo de permutaciones de un conjunto finito es el número de elementos en el conjunto. El ordende un grupo (de cualquier tipo) es el número de elementos (cardinalidad) en el grupo. Por el teorema de Lagrange , el orden de cualquier grupo de permutación finita de grado n debe dividirse n ! ( n - factorial , el orden del grupo simétrico S _n ).

Notación [ editar ]

Artículo principal: Permutación § Definición y uso.

Desde permutaciones son biyecciones de un conjunto, pueden ser representados por Cauchy 's de la notación de dos líneas . ^[4] Esta notación enumera cada uno de los elementos de M en la primera fila, y para cada elemento, su imagen bajo la permutación debajo de ella en la segunda fila. Si$${\ displaystyle \ sigma} Es una permutación del conjunto. $${\ displaystyle M = \ {x_ {1}, x_ {2}, \ ldots, x_ {n} \}} entonces,

{\ displaystyle \ sigma = {\ begin {pmatrix} x_ {1} & x_ {2} & x_ {3} & \ cdots & x_ {n} \\\ sigma (x_ {1}) & \ sigma (x_ {2}) & \ sigma (x_ {3}) & \ cdots & \ sigma (x_ {n}) \ end {pmatrix}}.

Por ejemplo, una permutación particular del conjunto {1,2,3,4,5} se puede escribir como:

{\ displaystyle \ sigma = {\ begin {pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 5 & 4 & 3 & 1 \ end {pmatrix}};}

esto significa que σ satisface σ (1) = 2, σ (2) = 5, σ (3) = 4, σ (4) = 3, y σ (5) = 1. Los elementos de M no tienen que aparecer en ningún orden especial en la primera fila. Esta permutación también podría escribirse como:

{\ displaystyle \ sigma = {\ begin {pmatrix} 3 & 2 & 5 & 1 & 4 \\ 4 & 5 & 1 & 2 & 3 \ end {pmatrix}}.

Las permutaciones a menudo también se escriben en notación cíclica ( forma cíclica ) ^{[5], de} modo que dado el conjunto M = {1,2,3,4}, una permutación g de M con g (1) = 2, g (2) = 4, g (4) = 1 y g (3) = 3 se escribirán como (1,2,4) (3), o más comúnmente, (1,2,4) ya que 3 no se modifica; Si los objetos se denotan con letras o dígitos individuales, también se pueden prescindir de comas y espacios, y tenemos una notación como (124). La permutación escrita arriba en notación de 2 líneas se escribiría en notación cíclica como$${\ displaystyle \ sigma = (125) (34).}

Composición de permutaciones - el producto del grupo [ editar ]

Artículo principal: Permutación § Permutaciones en la teoría de grupos.

El producto de dos permutaciones se define como su composición como funciones, en otras palabras, σ · π es la función que asigna cualquier elemento x del conjunto a σ ( π ( x )). Tenga en cuenta que la permutación más a la derecha se aplica al argumento primero, ^[6] [7] debido a la forma en que se escribe la aplicación de la función. Algunos autores prefieren que el factor más a la izquierda actúe primero, ^{[8] [9] [10],} pero para ello, las permutaciones deben escribirse a la derecha de su argumento, a menudo como superíndice , por lo que la permutación σ actúa sobre el elemento xresultados en la imagen x ^σ . Con esta convención, el producto viene dado por x ^{σ · π} = ( x ^σ ) ^π . Sin embargo, esto da una regla diferente para multiplicar permutaciones. Esta convención se usa comúnmente en la literatura de grupos de permutación, pero este artículo usa la convención donde se aplica primero la permutación más a la derecha.

Dado que la composición de dos bijections siempre da otra bijección, el producto de dos permutaciones es nuevamente una permutación. En la notación de dos líneas, el producto de dos permutaciones se obtiene reorganizando las columnas de la segunda permutación (más a la izquierda) de modo que su primera fila sea idéntica a la segunda fila de la primera permutación (más a la derecha). El producto se puede escribir como la primera fila de la primera permutación sobre la segunda fila de la segunda permutación modificada. Por ejemplo, dadas las permutaciones,

{\ displaystyle P = {\ begin {pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 4 & 1 & 3 & 5 \ end {pmatrix}} \ quad {\ text {and}} \ quad Q = {\ begin {pmatrix} 1 & 2 & 3 & 4 & 5 & l & 5 & 4 & 3 & 2 & 1 & end \ pmrix} ,}

El producto QP es:

{\ displaystyle QP = {\ begin {pmatrix} 1 & 2 & 3 & 4 & 5 \\ 5 & 4 & 3 & 2 & 1 & end {pmatrix}} \ {pmatrix}} {\ begin {pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 4 & 1 & 3 & 5 \ end {pmatrix}} = {\ begin {pmatrix} 1 & 2 & 3 & 4 & 5 \\ 4 & 2 & 5 & 3 & 1 \ end {pmatrix}}.}

La composición de las permutaciones, cuando se escriben en forma cíclica, se obtiene yuxtaponiendo las dos permutaciones (con la segunda escrita a la izquierda) y luego se simplifica a una forma de ciclo desunido si se desea. Así, en notación cíclica el producto anterior estaría dado por:

$${\ displaystyle Q \ cdot P = (15) (24) \ cdot (1243) = (1435).}

Como la composición de la función es asociativa , también lo es la operación del producto en las permutaciones: ( σ · π ) · ρ = σ · ( π · ρ ). Por lo tanto, los productos de dos o más permutaciones generalmente se escriben sin agregar paréntesis para expresar el agrupamiento; por lo general, también se escriben sin un punto u otro signo para indicar la multiplicación (los puntos del ejemplo anterior se agregaron para dar énfasis).

Elemento neutro e inversos [ editar ]

La permutación de identidad, que mapea cada elemento del conjunto a sí mismo, es el elemento neutral de este producto. En notación de dos líneas, la identidad es

{\ displaystyle {\ begin {pmatrix} 1 & 2 & 3 & \ cdots & n \\ 1 & 2 & 3 & \ cdots & n \ end {pmatrix}}.

En notación cíclica, e = (1) (2) (3) ... ( n ), que por convención también se denota con solo (1) o incluso (). ^[11]

Como las bijectiones tienen inversos , también lo hacen las permutaciones, y la inversa σ ⁻¹ de σ es nuevamente una permutación. Explícitamente, siempre que σ ( x ) = y uno también tiene σ ⁻¹ ( y ) = x . En la notación de dos líneas, se puede obtener la inversa intercambiando las dos líneas (y clasificando las columnas si se desea que la primera línea esté en un orden determinado). Por ejemplo

{\ displaystyle {\ begin {pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 5 & 4 & 3 & 1 \ end {pmatrix}} ^ {- 1} = {\ begin {pmatrix} 2 & 5 & 4 & 3 & 1 y 1 & 2 & 3 & 4 & 5 \ end {pmatrix}) \ 5 & 1 & 4 & 3 & 2 \ end {pmatrix}}.

Para obtener el inverso de un solo ciclo, revertimos el orden de sus elementos. Así,

$${\ displaystyle (125) ^ {- 1} = (521) = (152).}

Para obtener el inverso de un producto de ciclos, primero revertimos el orden de los ciclos, y luego tomamos el inverso de cada uno de los anteriores. Así,

$${\ displaystyle [(125) (34)] ^ {- 1} = (34) ^ {- 1} (125) ^ {- 1} = (43) (521) = (34) (152).}

Tener un producto asociativo, un elemento de identidad e inversos para todos sus elementos, hace que el conjunto de todas las permutaciones de M en un grupo , Sym ( M ); un grupo de permutación.

Ejemplos [ editar ]

Considere el siguiente conjunto G ₁ de permutaciones del conjunto M = {1,2,3,4}:

• e = (1) (2) (3) (4) = (1)
  • Esta es la identidad, la permutación trivial que corrige cada elemento.
• a = (1 2) (3) (4) = (1 2)
  • Esta permutación intercambia 1 y 2, y corrige 3 y 4.
• b = (1) (2) (3 4) = (3 4)
  • Como el anterior, pero cambiando 3 y 4, y arreglando los demás.
• ab = (1 2) (3 4)
  • Esta permutación, que es la composición de los dos anteriores, intercambia simultáneamente 1 con 2 y 3 con 4.

G ₁ forma un grupo, ya que aa = bb = e , ba = ab , y abab = e . Este grupo de permutación es isomorfo , como grupo abstracto, al grupo Klein V ₄ .

Como otro ejemplo consideremos el conjunto de simetrías de un cuadrado.. Deje que los vértices de un cuadrado estén etiquetados como 1, 2, 3 y 4 (en sentido contrario a las agujas del reloj alrededor del cuadrado comenzando con 1 en la esquina superior izquierda). Las simetrías están determinadas por las imágenes de los vértices, que, a su vez, pueden describirse mediante permutaciones. La rotación en 90 ° (en sentido contrario a las agujas del reloj) alrededor del centro del cuadrado se describe mediante la permutación (1234). Las rotaciones de 180 ° y 270 ° vienen dadas por (13) (24) y (1432), respectivamente. La reflexión sobre la línea horizontal a través del centro viene dada por (12) (34) y la reflexión de la línea vertical correspondiente es (14) (23). La reflexión sobre la línea 1,3 diagonal es (24) y la reflexión sobre la diagonal 2,4 es (13). La única simetría que queda es la identidad (1) (2) (3) (4). Este grupo de permutación se conoce de manera abstracta como el grupo diedro de orden 8.

Acciones de grupo [ editar ]

Artículo principal: Acción de grupo.

En el ejemplo anterior del grupo de simetría de un cuadrado, las permutaciones "describen" el movimiento de los vértices del cuadrado inducido por el grupo de simetrías. Es común decir que estos elementos de grupo están "actuando" en el conjunto de vértices del cuadrado. Esta idea se puede hacer precisa definiendo formalmente una acción grupal . ^[12]

Sea G un grupo y M un conjunto no vacío . Una acción de G en M es una función f : G × M → M tal que

• f (1, x ) = x , para todo x en M (1 es el elemento de identidad (neutral) del grupo G ), y
• f ( g , f ( h , x )) = f ( gh , x ), para todos g , h en G y todas las x en M .

Esta última condición también se puede expresar diciendo que la acción induce un homomorfismo de grupo de Ga Sym ( M ). ^[12] Cualquiera de tales homomorfismo se llama un (permutación) la representación de G en M .

Para cualquier grupo de la permutación, la acción que envía ( g , x ) → g ( x ) se llama la acción natural de G en M . Esta es la acción que se asume a menos que se indique lo contrario. ^[12] En el ejemplo del grupo de simetría del cuadrado, la acción del grupo en el conjunto de vértices es la acción natural. Sin embargo, este grupo también induce una acción en el conjunto de cuatro triángulos en el cuadrado, que son: t ₁ = 234, t ₂ = 134, t ₃ = 124 y t ₄ = 123. También actúa sobre las dos diagonales: d₁ = 13 y d ₂ = 24.

Elemento de grupo	Acción sobre triángulos.	Acción sobre diagonales.
(1)	(1)	(1)
(1234)	( t 1 t 2 t 3 t 4 )	( d 1 d 2 )
(13) (24)	( t 1 t 3 ) ( t 2 t 4 )	(1)
(1432)	( t 1 t 4 t 3 t 2 )	( d 1 d 2 )
(12) (34)	( t 1 t 2 ) ( t 3 t 4 )	( d 1 d 2 )
(14) (23)	( t 1 t 4 ) ( t 2 t 3 )	( d 1 d 2 )
(13)	( t 1 t 3 )	(1)
(24)	( t 2 t 4 )	(1)

El teorema de Cayley [ editar ]

Artículo principal: Teorema de Cayley.

Cualquier grupo G puede actuar sobre sí mismo (los elementos del grupo que se piensa como el conjunto M ) de muchas maneras. En particular, hay una acción regular dada por la multiplicación (izquierda) en el grupo. Es decir, f ( g , x ) = gx para todos g y x en G . Para cada fijo g , la función f _g ( x ) = gx es una biyección en G y por lo tanto una permutación del "set" G . Cada elemento de gpuede pensarse como una permutación de esta manera y, por lo tanto, G es isomorfo a un grupo de permutación; Este es el contenido del teorema de Cayley .

Considere el grupo G _{1 que} actúa sobre el conjunto {1,2,3,4} dado anteriormente. Deje que los elementos de este grupo se denoten por e , a , b y c = ab = ba . La acción de G ₁ sobre sí misma descrita en el teorema de Cayley da la siguiente representación de permutación:

f _e ↦ ( e ) ( a ) ( b ) ( c )

f _a ↦ ( ea ) ( bc )

f _b ↦ ( eb ) ( ac )

f _c ↦ ( ec ) ( ab ).

Permutación de grupos isomorfos [ editar ]

Si G y H son dos grupos de permutación en los conjuntos X e Y con acciones f ₁ y f ₂ respectivamente, entonces decimos que G y H son permutaciones isomorfas ( isomorfas como grupos de permutaciones ) si existe un mapa biyectivo λ  : X → Y y un isomorfismo grupal ψ  : G → H tal que: ^[13]

λ ( f ₁ ( g , x )) = f ₂ ( ψ ( g ), λ ( x )) para todo g en G y x en X .

Si X = Y esto es equivalente a que G y H se conjugan como subgrupos de Sym ( X ). ^[14] El caso especial donde G = H y ψ es el mapa de identidad da lugar al concepto de acciones equivalentes de un grupo. ^[15]

En el ejemplo de las simetrías de un cuadrado dado arriba, la acción natural en el conjunto {1,2,3,4} es equivalente a la acción en los triángulos. La bijección λ entre los conjuntos está dada por i ↦ t _i . La acción natural del grupo G ₁ anterior y su acción en sí misma (mediante la multiplicación de la izquierda) no son equivalentes, ya que la acción natural tiene puntos fijos y la segunda acción no.

Historia [ editar ]

Artículo principal: Historia de la teoría de grupos.

El estudio de los grupos originalmente surgió de una comprensión de los grupos de permutación. ^{[16] Las}permutaciones habían sido estudiadas intensamente por Lagrange en 1770 en su trabajo sobre las soluciones algebraicas de las ecuaciones polinómicas. Este tema floreció y, a mediados del siglo XIX, existía una teoría bien desarrollada de grupos de permutación, codificada por Camille Jordan en su libro Traité des Substitutions et des Équations Algébriques de 1870. El libro de Jordan se basaba, a su vez, en los documentos que quedaban por Évariste Galois en 1832.

Cuando Cayley introdujo el concepto de un grupo abstracto, no quedó inmediatamente claro si se trataba o no de una colección de objetos más grande que los grupos de permutación conocidos (que tenían una definición diferente de la moderna). Cayley continuó para demostrar que los dos conceptos eran equivalentes en el teorema de Cayley. ^[17]

Otro texto clásico que contiene varios capítulos sobre grupos de permutación es la Teoría de grupos de orden finita de Burnside de 1911. ^[18] La primera mitad del siglo XX fue un período de barbecho en el estudio de la teoría de grupos en general, pero el interés en los grupos de permutación fue revivido en la década de 1950 por H. Wielandt, cuyos apuntes de conferencias en alemán fueron reimpresos como Grupos de Permutación Finitaen 1964.