MECÁNICA CUÁNTICA

La ecuación de Bethe-Salpeter (llamada así por Hans Bethe y Edwin Salpeter ) ^[1] describe los estados ligadosde un sistema teórico de campo cuántico de dos cuerpos (partículas) en un formalismo relativísticamente covariante. La ecuación fue publicada por primera vez en 1950 al final de un artículo de Yoichiro Nambu , pero sin derivación. ^[2]

Una representación gráfica de la ecuación de Bethe-Salpeter.

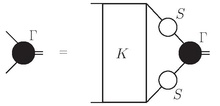
Debido a su generalidad y su aplicación en muchas ramas de la física teórica, la ecuación de Bethe-Salpeter aparece en muchas formas diferentes. Una forma, que se utiliza a menudo en la física de alta energía es

$${\ displaystyle \ Gamma (P, p) = \ int \! {\ frac {d ^ {4} k} {(2 \ pi) ^ {4}}} \; K (P, p, k) \, S (k - {\ tfrac {P} {2}}) \, \ Gamma (P, k) \, S (k + {\ tfrac {P} {2}})}

donde Γ es la amplitud de Bethe-Salpeter, K la interacción y S los propagadores de las dos partículas participantes.

En la teoría cuántica, los estados ligados son objetos que viven durante un tiempo infinito (de lo contrario se llaman resonancias ), por lo que los constituyentes interactúan infinitamente muchas veces. Al resumir, infinitas veces, todas las posibles interacciones que pueden ocurrir entre los dos constituyentes, la ecuación de Bethe-Salpeter es una herramienta para calcular las propiedades de los estados unidos. Su solución, la amplitud de Bethe-Salpeter, es una descripción del estado límite considerado.

Como se puede derivar a través de la identificación de estados límite con polos en la matriz S , se puede conectar a la descripción teórica cuántica de los procesos de dispersión y las funciones de Green .

La ecuación de Bethe-Salpeter es una herramienta teórica general del campo cuántico, por lo que las aplicaciones se pueden encontrar en cualquier teoría de campos cuánticos. Algunos ejemplos son el positronio(estado enlazado de un electrón - par de positrones ), los excitones ( estado enlazado de un par de orificios yelectrones ^[3] ) y los mesones (como estado enlazado de quark - antiquark). ^[4]

Incluso para sistemas simples como el positronio, la ecuación no se puede resolver exactamente, aunque en principio se puede formular exactamente. Se puede lograr una clasificación de los estados sin la necesidad de una solución exacta. Si una de las partículas es significativamente más masiva que la otra, el problema se simplifica considerablemente a medida que se resuelve la ecuación de Dirac para la partícula más ligera bajo el potencial externo de la partícula más pesada.

Derivación [ editar ]

El punto de partida para la derivación de la ecuación de Bethe-Salpeter es la ecuación de Dyson de dos partículas (o cuatro puntos)

$${\ displaystyle G = S_ {1} \, S_ {2} + S_ {1} \, S_ {2} \, K_ {12} \, G}

en el espacio de impulso, donde "G" es la función verde de dos partículas $${\ displaystyle \ langle \ Omega | \ phi _ {1} \, \ phi _ {2} \, \ phi _ {3} \, \ phi _ {4} | \ Omega \ rangle}, "S" son los propagadores libres y "K" es un núcleo de interacción, que contiene todas las interacciones posibles entre las dos partículas. El paso crucial ahora es asumir que los estados enlazados aparecen como polos en la función Verde. Se supone que dos partículas se juntan y forman un estado enlazado con una masa "M", este estado enlazado se propaga libremente y luego el estado enlazado se divide nuevamente en sus dos constituyentes. Por lo tanto, se introduce la función de onda Bethe-Salpeter. $${\ displaystyle \ Psi = \ langle \ Omega | \ phi _ {1} \, \ phi _ {2} | \ psi \ rangle}, que es una amplitud de transición de dos constituyentes $${\ displaystyle \ phi _ {i}} en un estado unido $${\ displaystyle \ psi}, y luego hace un ansatz para la función Verde en las proximidades del polo como

$${\ displaystyle G \ approx {\ frac {\ Psi \; {\ bar {\ Psi}}} {P ^ {2} -M ^ {2}}},}

donde P es el impulso total del sistema. Se ve, que si por este impulso la ecuación.$${\ displaystyle P ^ {2} = M ^ {2}}sostiene, lo que es exactamente la relación energía-momento de Einstein (con el Cuatro-impulso $${\ displaystyle P _ {\ mu} = \ left (E / c, {\ vec {p}} \ right)} y $${\ displaystyle P ^ {2} = P _ {\ mu} \, P ^ {\ mu}}) La función verde de cuatro puntos contiene un polo. Si se inserta esa respuesta en la ecuación de Dyson de arriba, y se establece el momento total "P" tal como se mantiene la relación energía-momento, en ambos lados del término aparece un polo.

$${\ displaystyle {\ frac {\ Psi \; {\ bar {\ Psi}}} {P ^ {2} -M ^ {2}}} = S_ {1} \, S_ {2} + S_ {1} \, S_ {2} \, K_ {12} {\ frac {\ Psi \; {\ bar {\ Psi}}} {P ^ {2} -M ^ {2}}}}

Comparando los rendimientos de los residuos.

$${\ displaystyle \ Psi = S_ {1} \, S_ {2} \, K_ {12} \ Psi, \,}

Esta ya es la ecuación de Bethe-Salpeter, escrita en términos de las funciones de onda de Bethe-Salpeter. Para obtener la forma anterior se introducen las amplitudes de Bethe-Salpeter "Γ"

$${\ displaystyle \ Psi = S_ {1} \, S_ {2} \, \ Gamma}

y finalmente se pone

$${\ displaystyle \ Gamma = K_ {12} \, S_ {1} \, S_ {2} \, \ Gamma}

que se anota arriba, con la dependencia explícita del impulso.

Aproximación de escalera [ editar ]

Una representación gráfica de la ecuación de Bethe-Salpeter en aproximación de escalera

En principio, la interacción Kernel K contiene todas las posibles interacciones irreductibles de dos partículas que pueden ocurrir entre los dos constituyentes. Por lo tanto, en los cálculos prácticos uno tiene que modelarlo y solo elegir un subconjunto de las interacciones. Al igual que en las teorías de campos cuánticos , la interacción se describe mediante el intercambio de partículas (por ejemplo, fotones en la electrodinámica cuántica o gluones en la cromodinámica cuántica ), la interacción más simple es el intercambio de una sola de estas partículas de fuerza.

Como la ecuación de Bethe-Salpeter resume la interacción infinitas veces, la gráfica de Feynman resultante tiene la forma de una escalera.

Mientras que en la electrodinámica cuántica la aproximación de la escala causó problemas al cruzar la simetría y la invariancia de los indicadores y, por lo tanto, se tuvieron que incluir los términos de la escala cruzada, en la cromodinámica cuántica esta aproximación se usa fenomenológicamente bastante para calcular las masas de hadrones , ^[4] ya que respeta la ruptura de simetría quiral y por lo tanto es una parte importante de la generación de estas masas.

Normalización [ editar ]

Como para cualquier ecuación homogénea, la solución de la ecuación de Bethe-Salpeter se determina solo hasta un factor numérico. Este factor tiene que ser especificado por una cierta condición de normalización. Para las amplitudes de Bethe-Salpeter, esto suele hacerse exigiendo la conservación de la probabilidad (similar a la normalización de la función de onda mecánica cuántica ), que corresponde a la ecuación ^[5]

$${\ displaystyle 2P _ {\ mu} = {\ bar {\ Gamma}} \ left ({\ frac {\ partial} {\ partial P _ {\ mu}}} \ left (S_ {1} \ otimes S_ {2} \ derecha) -S_ {1} \, S_ {2} \, \ izquierda ({\ frac {\ parcial} {\ parcial P _ {\ mu}}} \, K \ derecha) \, S_ {1} \, S_ {2} \ derecha) \ Gamma}

Las normalizaciones de la carga y el tensor de energía-momento del estado unido llevan a la misma ecuación. En la aproximación de escalera, el núcleo de interacción no depende del impulso total de la amplitud de Bethe-Salpeter, por lo que, para este caso, el segundo término de la condición de normalización desaparece.

La física de cadenas de bits es un cuerpo de teoría que supone que la realidad puede representarse mediante un proceso de operaciones en cadenas finitas de símbolos dicotómicos, o bits (1 y 0). La física de cadenas de bits se ha desarrollado a partir del descubrimiento de Frederick Parker-Rhodes en 1964 de la jerarquía combinatoria : cuatro números producidos a partir de un algoritmo recursivo puramente matemático que corresponde a las fuerzas relativas de las cuatro fuerzas . Estas fortalezas se caracterizan por las constantes de acoplamiento fuerte, débil, electromagnética ( constante de estructura fina ) y gravitacional . ^[1]Otros contribuyentes principales en el campo son H. Pierre Noyes , Ted Bastin , Clive W. Kilmister , John Amson, Mike Manthey y David McGoveran . ^[1] [2]

En un documento de 2001 de Noyes, se presentaron pruebas de las predicciones hechas por la teoría que se confirmaron más tarde.

La teoría de Bohr-Kramers-Slater ( teoría BKS) fue quizás el intento final de comprender la interacción de la materia y la radiación electromagnética sobre la base de la llamada teoría cuántica antigua , en la que se tratan los fenómenos cuánticos mediante la imposición de restricciones cuánticas en la descripción clásica. comportamiento. ^{[1] [2] [3]} Fue avanzado en 1924 y se adhiere a una descripción de onda clásica del campo electromagnético. Tal vez fue más un programa de investigación que una teoría física completa, ya que las ideas que se desarrollan no se desarrollan de manera cuantitativa. ^[4] : 236

Un aspecto, la idea de modelar el comportamiento atómico bajo radiación electromagnética incidente usando "osciladores virtuales" en las frecuencias de absorción y emisión, en lugar de las (diferentes) frecuencias aparentes de las órbitas de Bohr, llevó significativamente a Born , Heisenberg y Kramers a explorar matemáticas que Inspiró el desarrollo posterior de la mecánica matricial , la primera forma de la mecánica cuántica moderna . La provocación de la teoría también generó una gran discusión y renovó la atención a las dificultades en los fundamentos de la vieja teoría cuántica. ^[5] Sin embargo, físicamente, el elemento más provocativo de la teoría, que el impulso y la energía no necesariamente se conservarían en cada interacción, sino que, en general, estadísticamente, pronto se mostró que estaba en conflicto con el experimento.

Orígenes [ editar ]

La idea inicial de la teoría BKS se originó con Slater , ^[6] que propuso a Bohr y Kramers los siguientes elementos de una teoría de emisión y absorción de radiación por átomos, que se desarrollará durante su estancia en Copenhague:

1. La emisión y absorción de radiación electromagnética por la materia se realiza de acuerdo con el concepto de fotones de Einstein ;
2. Un fotón emitido por un átomo es guiado por un campo electromagnético clásico (compare las ideas de Broglie publicadas en septiembre de 1923 ^[7] ) que consiste en ondas esféricas, lo que permite explicar la interferencia ;
3. Incluso cuando no hay transiciones, existe un campo clásico al que contribuyen todos los átomos; este campo contiene todas las frecuencias en las que un átomo puede emitir o absorber un fotón, la probabilidad de que dicha emisión esté determinada por la amplitud de la componente de Fouriercorrespondiente del campo; el aspecto probabilístico es provisional, y se eliminará cuando la dinámica del interior de los átomos sea más conocida;
4. El campo clásico no se produce por los movimientos reales de los electrones, sino por "movimientos con las frecuencias de posibles líneas de emisión y absorción " (que se denominarán " osciladores virtuales ", creando un campo al que también se hará referencia como "virtual") .

Desarrollo con Bohr y Kramers [ editar ]

Esta sección necesita citas adicionales para su verificación . Por favor, ayudar a mejorar este artículo mediante la adición de citas de fuentes confiables . El material sin fuente puede ser desafiado y eliminado.  Encuentre fuentes:  "Teoría de BKS"  -  noticias  · periódicos  · libros  · erudito  · JSTOR (octubre de 2018 ) ( Aprenda cómo y cuándo eliminar este mensaje de plantilla )

La intención principal de Slater parece haber sido reconciliar los dos modelos conflictivos de radiación, a saber. Los modelos de onda y de partículas . Puede haber tenido buenas esperanzas de que su idea con respecto a los osciladores que vibran ante las diferencias de las frecuencias de rotación de electrones (en lugar de las frecuencias de rotación en sí mismas) pueda ser atractiva para Bohr porque resolvió un problema del modelo atómico de este último , aunque El significado físico de estos osciladores estaba lejos de ser claro. Sin embargo, Bohr y Kramers tuvieron dos objeciones a la propuesta de Slater:

1. El supuesto de que existen los fotones. Aunque la hipótesis de los fotones de Einstein podría explicar de manera simple el efecto fotoeléctrico , así como la conservación de la energía en los procesos de desinfección de un átomo seguido de la excitación de un vecino, Bohr siempre se había mostrado reacio a aceptar la realidad de los fotones. Su principal argumento es el problema de conciliar la existencia de fotones con el fenómeno de la interferencia ;
2. La imposibilidad de explicar la conservación de la energía en un proceso de desexcitación de un átomo seguido de la excitación de un vecino. Esta imposibilidad se desprendió del supuesto probabilístico de Slater, que no implicaba ninguna correlación entre los procesos que tienen lugar en átomos diferentes.

Como lo expresa Jammer, esto volvió a enfocar la teoría "para armonizar la imagen física del campo electromagnético continuo con la imagen física, no como Slater había propuesto de los cuantos de luz, sino de las transiciones cuánticas discontinuas en el átomo". ^[5] Bohr y Kramers esperaban poder evadir la hipótesis del fotón sobre la base del trabajo en curso de Kramers para describir la "dispersión" (en términos actuales de dispersión inelástica ) de la luz por medio de una teoría clásica de la interacción de la radiación y importar. Pero abandonando el concepto del fotón, en su lugar optaron por aceptar de lleno la posibilidad de no conservación de la energía y el impulso.

Contra-evidencia experimental [ editar ]

En el documento BKS, el efecto Compton se discutió como una aplicación de la idea de " conservación estadística de energía y momento" en un proceso continuo de dispersión de radiación por una muestra de electrones libres, donde "cada uno de los electrones contribuye a través de la emisión de Ondas secundarias coherentes ". Si bien Compton ya había dado una explicación atractiva de su experimento sobre la base de la imagen del fotón (incluida la conservación de la energía y el impulso en los procesos de dispersión individual ), se afirma en el documento BKS que "parece que en el estado actual de la ciencia no es justificable". rechazar una interpretación formal como la que se está considerando [es decir, el supuesto más débil de las estadísticasconservación "como inadecuada". Esta afirmación puede haber llevado a los físicos experimentales a mejorar "el estado actual de la ciencia" al probar la hipótesis de "energía estadística y conservación del momento". En cualquier caso, ya después de un año, la teoría BKS fue refutada por experimentos estudiando las correlaciones entre las direcciones en las que se emiten la radiación emitida y el electrón de retroceso en procesos de dispersión individuales. Estos experimentos fueron realizados de forma independiente por Bothe y Geiger , ^[8] , así como por Compton y Simon. ^[9]Proporcionaron evidencia experimental que apunta en la dirección de la conservación de la energía y el momento en los procesos de dispersión individual (al menos, se demostró que la teoría BKS no podía explicar los resultados experimentales). Experimentos más precisos, realizados mucho más tarde, también han confirmado estos resultados. ^[10] [11]

Como lo sugirió una carta a Born , ^[12] para Einstein, la corroboración de la conservación de la energía y el momento fue probablemente aún más importante que su hipótesis de fotones: "La opinión de Bohr sobre la radiación me interesa mucho. Pero no quiero dejarme ser. impulsado a renunciar a la causalidad estricta antes de que haya habido una resistencia mucho más fuerte en su contra que hasta ahora. No puedo soportar la idea de que un electrón expuesto a un rayo debe, por propia decisión libre, elegir el momento y la dirección en que quiere para saltar. Si es así, prefiero ser un zapatero o incluso un empleado en una casa de juego que un físico. Es cierto que mis intentos de dar la forma palpable a los cuantos han fallado una y otra vez, pero no voy a hacerlo. renunciar a la esperanza durante mucho tiempo todavía ".

La reacción de Bohr tampoco estaba relacionada principalmente con la hipótesis del fotón. Según Heisenberg , ^[13] Bohr comentó: "Incluso si Einstein me envía un cable que ahora se ha encontrado una prueba irrevocable de la existencia física de los cuantos de luz, el mensaje no puede alcanzarme, porque tiene que ser transmitido por ondas electromagnéticas. . " Para Bohr, la lección que se aprendió de la refutación de la teoría BKS no fue que los fotones existen, sino que la aplicabilidad de las imágenes clásicas del espacio-tiempo para comprender los fenómenos dentro del dominio cuántico es limitada. Este tema se volvería particularmente importante unos años más tarde al desarrollar la noción de complementariedad . Según Heisenberg, la interpretación estadística de Born.También tuvo sus raíces últimas en la teoría BKS. Por lo tanto, a pesar de su fracaso, la teoría de BKS todavía proporcionó una contribución importante a la transición revolucionaria de la mecánica clásica a la mecánica cuántica .